Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Zero
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we'll focus on the number zero, particularly its role as an additive identity. When we say something is an additive identity, what does that mean?

Does it mean it doesn’t change the number when it's added?

Exactly! For instance, if we take any number, like 5, and add zero, we get back 5. This can be illustrated as 5 + 0 = 5. Can you think of another example?

How about 10 + 0, which also equals 10?

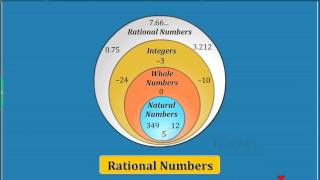
Great! So, we see this is true for whole numbers. What about integers? Can someone give an example using integers?

-3 + 0 = -3.

Great example! So, we see that zero works the same way across whole numbers and integers. Let’s summarize our key points.
Zero and Rational Numbers
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now, let’s extend our understanding of zero to rational numbers. Can anyone explain how zero interacts with rational numbers?

If we add zero to a fraction, it should stay the same, right?

Exactly! For instance, if we have -2/3 and add zero, we still have -2/3. This means for any rational number 'c', the addition c + 0 = c holds true. Why is this property important?

It helps to show that zero doesn't change the value when we perform operations.

Correct! Let’s remember that zero is called the additive identity. Each time we add zero, we return to our original number.
Applications of the Additive Identity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Knowing zero’s role as an identity element can greatly help in simplified calculations. Can anyone recall how this understanding can assist in solving equations?

If we know a + 0 = a, it makes it easier when we see equations that have zero in them.

Yes! It helps reduce complexity. For instance, in an equation like x + 0 = 5, we immediately identify that x must be 5. Let's reinforce this with a small quiz!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section emphasizes zero's unique role in mathematics as the additive identity, demonstrating how it maintains any number's value when added. It is a fundamental element in understanding numerical operations across different sets of numbers.
Detailed
In this section, we explore the role of zero (0) in various numerical contexts. Zero is introduced as an additive identity, a concept that means adding zero to any number does not change the value of that number. We observe this property across whole numbers, integers, and rational numbers with examples such as:
- For whole numbers, 2 + 0 = 2.
- For integers, -5 + 0 = -5.
- For rational numbers, adding 0 to them also results in the original number, illustrated by -2 + (0 × -2/7) = -2.
This exemplifies that for any real number 'a', the equation a + 0 = a holds true. Thus, zero is recognized as the additive identity in mathematics, which is crucial for operations involving different types of numbers. Its understanding is essential when exploring operations in rational numbers, reinforcing its foundational importance in the arithmetic structure of mathematics.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Addition of Zero to Whole Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
2 + 0 = 0 + 2 = 2 (Addition of 0 to a whole number)
Detailed Explanation
When we add zero to any whole number, the sum is always the original whole number. This is because zero does not change the value of the number it is added to. The example 2 + 0 shows this clearly. No matter how you arrange it (0 + 2), the result remains 2.
Examples & Analogies
Imagine you have two apples. If you add 0 apples to your collection, you'll still have two apples. It's like a situation where you don’t gain or lose anything; the total remains the same.
Addition of Zero to Integers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
– 5 + 0 = ... + ... = – 5 (Addition of 0 to an integer)
Detailed Explanation
The same principle applies to integers. For instance, if we have -5 and we add 0, the equation -5 + 0 still equals -5. Again, this demonstrates that zero does not affect the value of the original integer.
Examples & Analogies
If you owe someone $5 (represented as -5), and you don't add any more debt (adding 0), you still owe $5. Adding zero changes nothing—your debt remains the same!
Addition of Zero to Rational Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
−2 + ... = 0 + (−2/7) = (Addition of 0 to a rational number)
Detailed Explanation
In the case of rational numbers, like -2 or -2/7, adding zero will yield the same rational number. For example, -2 + 0 results in -2. Whether you're using simple integers or fractions, zero's role remains as the number that leaves the quantity unchanged.
Examples & Analogies
Think of measuring something, say -2 meters below sea level. If you add 0 meters more (a zero-length rope), you still are at -2 meters below. Nothing changes regardless of how you look at it.
Identity Property of Addition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In general, a + 0 = 0 + a = a, where a is a whole number. b + 0 = 0 + b = b, where b is an integer. c + 0 = 0 + c = c, where c is a rational number.
Detailed Explanation
This principle can be summarized as the identity property of addition, which states that adding zero to any number does not change that number. This property holds for all types of numbers: whole numbers, integers, and rational numbers.
Examples & Analogies
It's like having a birthday cake with your favorite flavor. If someone brings an additional cake with zero added flavors, your original cake's flavor doesn't change—it remains your favorite. Zero adds nothing extra!
Zero as the Additive Identity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Zero is called the identity for the addition of rational numbers. It is the additive identity for integers and whole numbers as well.
Detailed Explanation
Since adding zero to any rational number, whole number, or integer results in the original number, zero is described as the additive identity. It is the 'neutral' number in addition—making it crucial in arithmetic.
Examples & Analogies
Envision a neutral friend in a game. Their presence doesn't alter the score; they simply maintain balance. Similarly, zero doesn't modify any number during addition, ensuring everything stays intact.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Zero is the additive identity: Adding zero to any number leaves it unchanged.
-
Zero's role is consistent across whole numbers, integers, and rational numbers.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example: 5 + 0 = 5 illustrates that when zero is added to five, the result is still five.
-
Example: For the rational number -3/4, adding zero gives -3/4.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Adding zero, hear me say, keeps the same number all day!
📖 Fascinating Stories
-
Imagine a basket of apples. If you add zero apples, how many do you have? Just the same number of apples in the basket!
🧠 Other Memory Gems
-
Remember 'Z' for zero stands for the 'Z' in 'Same'. Zero does not change value.
🎯 Super Acronyms
I.Z.Z.Y
- Zero Is an Zany Identity
- it keeps numbers unchanged!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Identity Element
Definition:
An element that, when combined with another element, does not change the value; in this case, '0' for addition.
-
Term: Additive Identity
Definition:
The value that does not change a number when added to it, which is zero in this context.

