Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mathematical Modeling in Elastic Rebound
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore how we can use mathematics to model the elastic rebound, which helps us understand the behavior of earthquakes. Why do you think mathematical modeling is important in this context?
I think it helps us predict earthquakes better!
And it might help in designing buildings that can survive them!
Exactly! The more accurately we can model elastic rebound, the better we can prepare for seismic events. One of the key models we use is the dislocation theory. Can anyone tell me what a dislocation in geoscience might refer to?
Isn't it about how rocks move and slip along faults?
Absolutely, dislocations represent those movements. They’re fundamental to understanding how strain and stress accumulate in the crust.
Now, let's familiarize ourselves with the key equation used in modeling surface displacement: $$ u(x) = \frac{D}{\pi(x^2 + h^2)} $$. Who can help me break down what these variables mean?
I remember! **u(x)** is the surface displacement, **D** is the fault slip, and **h** is the depth, right?
Correct! Keep this equation in mind as it will help you visualize Earth’s response to faults. This equation showcases how the displacement diminishes with distance. Great work, everyone! Remember the acronym DHD: **D**isplacement, **H**eight (meaning depth), **D**istance. This can help you remember the key elements.
Understanding Surface Displacement through Mathematical Models
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's explore deeper into how our equation, $$ u(x) = \frac{D}{\pi(x^2 + h^2)} $$, illustrates surface displacement. How does fault slip influence the displacement observed at the surface?
I think the greater the fault slip **D**, the more displacement **u(x)** we observe!
Exactly, and what about the relationship with distance **x**? How does that affect the displacement?
If you're farther from the fault, the displacement should be less, right?
Correct! The equation reflects that property where displacement decreases as distance from the fault increases. This decay of effects is critical in earthquake engineering to determine safe distances for buildings. Can anyone think of real-world applications of this knowledge?
We can use it to set boundaries for construction zones!
And help in evacuation planning for earthquakes!
Great points! Hence, understanding and applying these mathematical models is not just theoretical; it's crucial for saving lives and infrastructure.
Evaluating the Limitations of Mathematical Models
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
While mathematical modeling is powerful, let's discuss its limitations in the context of elastic rebound. How might these models fall short in predicting real earthquakes?
Maybe they can’t account for all the complex factors in the Earth's crust?
Exactly! Factors like fault complexity, material properties, and other geological features can affect predictions. Additionally, what do we say about the behavior of some faults that may not show traditional elastic rebound?
They could exhibit aseismic creep instead, releasing stress gradually.
Right! This reinforces the idea that while models help us understand potential behaviors, they don't capture every scenario. Therefore, continuous adjustments and refinements in modeling are necessary. Remember, models are tools, not crystal balls!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, various mathematical models of elastic rebound are explored, emphasizing dislocation theory, elastic half-space models, and specific equations used to calculate surface displacement. These models help in understanding fault mechanics and predicting seismic activity.
Detailed
Mathematical Modeling of Elastic Rebound
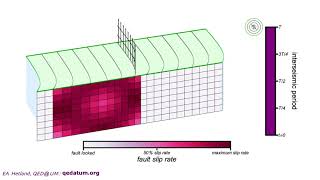
In the study of elastic rebound, quantitative approaches allow scientists and engineers to model the behavior of Earth’s crust during seismic activities. Key mathematical frameworks that describe this phenomenon include dislocation theory, elastic half-space models, and Okada equations. The displacement caused by a fault slip, for instance, can be expressed using a fundamental equation:
$$ u(x) = \frac{D}{\pi(x^2 + h^2)} $$
Where:
- u(x) corresponds to the surface displacement at a horizontal distance x from the fault,
- D represents the slip on the fault,
- h signifies the depth of the fault.
These mathematical models are crucial for predicting the effects of fault movements on the surface and for assessing associated seismic hazards, aiding both theoretical studies and practical applications in earthquake engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Mathematical Modeling
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Elastic rebound can be quantitatively modeled using:
• Dislocation theory
• Elastic half-space models
• Okada equations for calculating surface deformation due to fault slip.
Detailed Explanation
Mathematical modeling of elastic rebound helps us predict how the Earth's crust behaves in response to tectonic forces. Several methods can be used, such as dislocation theory, which models the fault as a dislocation in material, elastic half-space models that simplify the Earth's crust into layers, and Okada equations that provide specific calculations for ground deformation when a fault slips.
Examples & Analogies
Think of an elastic band. If you stretch it, it bends and stores energy. When you release it, it snaps back to its original shape. Similarly, mathematical modeling helps predict how the Earth's crust deforms and rebounds like that elastic band when tectonic forces are applied.
Surface Displacement Model
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example: The displacement u(x) due to a fault slip D at depth h in an elastic half-space can be modeled as:
D h
u(x)= ·
π x2+h2
Where:
• u(x): Surface displacement at a horizontal distance x from the fault
• D: Slip on the fault
• h: Depth of fault
Detailed Explanation
This formula shows how fault slip at a certain depth causes surface displacement. Here, 'u(x)' is the displacement that occurs at a distance 'x' from the fault line. The variables 'D' (the amount the fault slips) and 'h' (the depth of the fault) influence how much the surface actually moves. The equation uses π, which is a mathematical constant that often appears in problems involving circles, indicating that the model considers circular displacement around the fault.
Examples & Analogies
Imagine you're standing still with a rubber mat under your feet. If someone pulls the mat (representing the fault slip) at a certain depth, the surface you stand on moves based on how far they pulled it and how deep the mat is. The further away from the pull (the fault), the less noticeable the movement is at your position, just like how the displacement decreases with distance in the formula.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
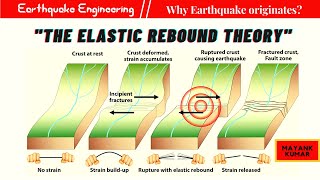
Elastic Rebound: The sudden release of stored energy in the Earth's crust during an earthquake.
-
Dislocation Theory: A mathematical model explaining fault movement and displacement.
-
Surface Displacement: The observable change in position on the Earth’s surface resulting from fault activity.
-
Okada Equations: Essential equations for quantifying surface deformation due to fault slip.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The calculation of displacement using the Okada equations for a known fault slip to assess potential damages in surrounding areas.
-
Utilizing dislocation theory to model earthquake frequency and potential hazards in populated regions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Fault slips and shifts, rocks will sway, / Math models help keep hazards at bay.
📖 Fascinating Stories
-
Imagine a rubber band stretched too far; when it snaps back, it mimics how a fault behaves during an earthquake.
🧠 Other Memory Gems
-
Remember DHD: Displacement, Height (depth), and Distance to recall the key elements of fault modeling.
🎯 Super Acronyms
Use the acronym SDO (Slip-Depth-Distance) to remember critical variables in assessing surface displacement.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Elastic Rebound
Definition:
A theory explaining how deformed rock masses release built-up energy as they return to their original shape during earthquakes.
-
Term: Dislocation Theory
Definition:
A framework for modeling the displacement of rock masses during fault movement.
-
Term: Elastic HalfSpace Model
Definition:
A mathematical model that assumes the Earth's surface behaves like an elastic medium.
-
Term: Okada Equations
Definition:
A set of equations used to calculate surface displacement caused by fault movement in an elastic half-space.