Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Box Models
Unlock Audio Lesson
Welcome everyone! Today, we're diving into the concept of box models. Can anyone tell me what they think a box model is?
Is it like creating boxes in a system to analyze something?
Exactly! We use these 'boxes' to simplify complex systems. A box model helps us understand the transport and fate of pollutants by treating sections of a water body as individual units.
What kind of pollutants are we talking about?
Great question! Pollutants can be chemicals from industrial sources, sewage, or even fertilizers. Now, can anyone give me examples of how a box model can depict movement or reactions within a water system?
I think it would show how pollutants are absorbed or broken down over time.
Precisely! The box models track changes using specific equations related to inflow and outflow. This leads us to remember: 'Define, Model, Analyze'—our three steps.
So, if the box model is defined correctly, we can get a good picture of the entire system?
Absolutely, and that leads us to the importance of boundary conditions. Remember the phrase: 'Define your boundaries, understand your system!'
Let's summarize—box models simplify systems to analyze pollutant transport effectively, and boundaries help define our domain of study.
Mass Balance in Box Models
Unlock Audio Lesson
Moving on, let's talk about mass balance. Who can explain what mass balance means in the context of box models?
Isn't it about how much pollutant enters and leaves a box over time?
Exactly! In mathematical terms, we often express it as: Rate In – Rate Out = Accumulation. Can anyone tell me why this setup is crucial?
It helps us understand if a box is gaining or losing pollutants.
Correct! This concept allows us to create predictive models. It's key to remember: 'In, Out, and Accumulate' for understanding.
What other factors can affect this balance?
Good point! Factors like reaction rates, temperature, and flow rates can all impact our calculations. If we say 'Flux per Area' instead of 'Rate', how does that change our perspective?
It focuses more on the transport rather than just simple rates.
Exactly! Flux integrates the area into our considerations. So, in summary, mass balance is essential for understanding both incoming and outgoing pollutants, influenced by various factors.
Challenges with Large Systems
Unlock Audio Lesson
Now, let's delve into larger systems, like air quality. What makes modeling air different from water bodies?
Maybe there are no clear boundaries like in lakes or rivers?
That's right! Air is expansive, making it tricky to define where our box begins and ends. Without boundaries, how can we model effectively?
Perhaps focusing on regions instead of strict boundaries?
Exactly! We can treat certain regions, like above a city, as a defined volume. What's important to remember about mixing in the atmosphere?
There are various layers and mixing heights that can impact how pollutants spread.
Correct! Mixing height is essential for determining how pollutants are distributed and diluted in the atmosphere. Think of 'Vertical Influence'—it’s a key concept in air quality.
So, mixing heights change depending on weather too?
Precisely! Factors like temperature differences and wind contribute to convection, impacting our models. Our takeaway? Understanding boundaries and mixing creates the backbone for accurate modeling strategies.
Concepts of Convection and Mixing
Unlock Audio Lesson
Let's explore convection! Who can explain what convection is?
Is it how heat moves in fluids?
Yes! In environmental contexts, it also pertains to pollutant transport. It’s essential to recognize how heat and wind can cause mixing. How does this relate to our box models?
It means that convection can distribute pollutants within a box or across boxes in our model.
Exactly! The more convection, the more homogenization occurs. Remember the acronym S.H.A.P.E—Speed, Heat, Air, Pollutant, Exchange—for factors that influence convection.
So more kinetic energy generally means better mixing, right?
Correct! Higher kinetic energy increases turbulence, enhancing mixing. What does this mean for pollutant levels in different air layers?
It could lead to higher concentrations at lower levels if mixing doesn’t happen effectively.
Good observation! Understanding convection's role is critical for accurate pollutant modeling. Let’s recap: Convection leads to distributed mixing, significantly impacting pollutant levels.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Box models serve as a strategic approach to understanding pollutant fate and transport within defined environmental systems, such as lakes and rivers. This section explains how these models integrate various physical and chemical processes, emphasizing the need for precise system definitions and the challenges posed by varying environmental conditions.
Detailed
In the study of environmental quality, box models are essential tools for analyzing the fate and transport of pollutants, especially in water bodies. These models simplify the real world by creating defined domains where processes such as reaction rates, inflow, and boundary conditions are illustrated. The section details components necessary for successful modeling, including the identification of initial conditions, boundary conditions, and dimensional factors that affect pollutant flow.
Specifically, the box model approach involves breaking down a larger system into smaller volumes (or 'boxes') where mass transfer and flux calculations occur. This can be complex in dynamic systems like rivers where properties can vary with time and space, as well as in air quality models where boundaries are not as clearly defined.
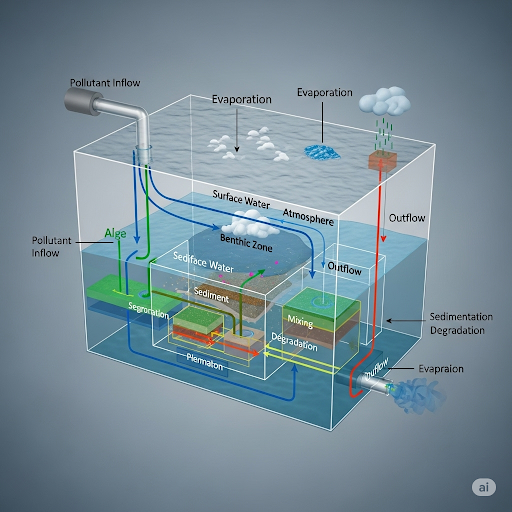
The section also highlights the role of convection and other mixing processes that affect pollutant distribution in both water and air, explaining the importance of mixing height and introducing concepts such as the boundary layer. Overall, the discussion provides insight into the practical implications and challenges of using box models for environmental monitoring and pollution control.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Box Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Okay, so we will continue from what we were discussing last week. We were discussing box models. So, the box model essentially is a convenient way of handling fate and transport of pollutants in a large system.
Detailed Explanation
A box model is a simplified representation that helps in understanding how pollutants are transported and behave in a large environment, like a lake or a river. By treating different parts of the system as 'boxes,' we can analyze how substances move and change within those sections.
Examples & Analogies
Imagine a series of containers, each filled with water and having some colored dye mixed in. Each container represents a 'box,' and as you pour dye into one, it spreads through that box. The way the dye disperses in each box helps us understand how pollutants might spread in a natural body of water.
Defining the System and Objectives
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, in general when you are trying to model a large system, the general rule of modeling is following. So, you have to define a system domain, it is where some processes are happening. Your goal is to find out concentration as the function of x, y, z and time t.
Detailed Explanation
Modeling a system requires setting boundaries and defining where processes occur. The goal is to understand how the concentration of pollutants changes over time and across different three-dimensional coordinates (x, y, z). This involves knowing the initial conditions and any factors affecting the system, like reactions or inflow.
Examples & Analogies
Think of a city where you need to analyze air quality. First, you define the area's limits (the city boundary). Then, you track how pollution levels change over time and from different locations within the city, similar to how an artist would study the landscape while painting.
Equation and Boundaries
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the system domain, there is an equation that will describe what is happening in the system. The system definition for say environmental system water is, for example, if you take a lake it is very nice very well defined boundary.
Detailed Explanation
An equation is crucial to model the behavior of pollutants within the defined boundaries of the system. For instance, in a well-defined system like a lake, pollutants can be tracked based on physical and chemical properties. This helps in understanding how pollutants interact within a specific area.
Examples & Analogies
Imagine trying to map how smoke from a factory spreads in a lake. The factory is well-defined within a certain boundary, allowing scientists to create equations that model how the pollutants disperse through the water.
Inflow, Outflow, and Rate of Reaction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we are talking about rate in, we use this term Q. This Q is flow rate of water that may be changing because there may be an inflow of some other stream.
Detailed Explanation
It's essential to consider both inflow and outflow of materials as they affect the concentration of pollutants. The flow rate (Q) can change, influencing how pollutants are transported, causing reactions that further alter their composition over time.
Examples & Analogies
Think of a bathtub: if you leave the tap running while also draining water, the levels change based on the flow rate of both. This constant change can affect how the bathwater (representing the pollutants) is mixed depending on how much and how fast water flows in and out.
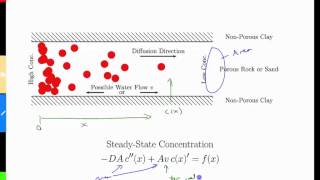
Flux and Mass Transfer
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When we say rate, we say the mass balance is written in terms of rate equals flux into area. The reason we do this is this is a convenient way of expressing mass transfer from different places.
Detailed Explanation
In pollution modeling, flux refers to the amount of material passing through a specific area over time. Understanding flux helps to apply mass balance equations, which are crucial in modeling how pollutants are distributed and transported in a system.
Examples & Analogies
Imagine a river as a conveyor belt that carries trash down its length. The amount of trash flowing through each section depends on how fast it moves and how wide the conveyor is. By calculating this 'flux', we can predict where pollution will be more concentrated.
Complexities of Air Quality Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When we go from a river kind of system to air, we do not have a physical boundary as air exists throughout.
Detailed Explanation
Modeling air quality is significantly more complex than modeling water because air has no defined edges. This makes it challenging to apply box models as pollutants might enter and exit the system at various points in an infinite volume.
Examples & Analogies
Imagine trying to predict how smoke from a barbecue spreads in an open park versus how it behaves in a closed room. In the park, the smoke disperses freely and can go in many directions, making it hard to track or contain.
Defining the Mixing Height
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The vertical extent to which you can consider your box model depends on what we call as mixing height. This is supposed to be the dimension where your vertical extent of box model is.
Detailed Explanation
Mixing height refers to the altitude at which pollutants are assumed to be evenly distributed in the air column. Understanding mixing height is crucial to accurately estimate pollutant concentrations within the air space above the Earth’s surface.
Examples & Analogies
Think of baking soda in water. Initially, if sprinkled on the surface, it sinks, but over time it mixes through the entire volume. The mixing height would be the depth at which it effectively distributes itself throughout the water body.
Convection and Pollution Dispersal
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Convection is essentially moving in circles and can be influenced by temperature and density differences.
Detailed Explanation
Convection significantly influences how pollutants disperse in the air. The process involves warmer, lighter air rising and cooler, denser air sinking, creating a circulation pattern that helps to mix pollutants vertically.
Examples & Analogies
Consider how hot air balloons work. As the air inside the balloon heats up, it rises. Similarly, in the atmosphere, warm air rises, carrying pollutants with it, which is a natural convection process.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Box Models: Simplified systems used to understand pollutant transport.
-
Mass Balance: The principle of tracking substances entering and leaving a defined system.
-
Flux: A measure of the flow of materials over a specific area.
-
Mixing Height: The vertical region where air pollutants are evenly distributed.
-
Convection: The process driving the movement and mixing of air and pollutants.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using box models to analyze pollutant distribution in a lake, considering inflows from nearby rivers and sewage.
-
Applying the concept of mass balance to evaluate how much of a pollutant remains in a body of water over time, accounting for decay rates.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In boxes we find, pollutants unwind, transport them around, in systems well-bound.
📖 Fascinating Stories
-
Imagine a polluted lake divided into sections, where each box holds secrets of chemical interactions, helping scientists track pollutant paths over time.
🧠 Other Memory Gems
-
B.M.F.C.: Box Models for Fluid Convection—helping us recall the main themes of pollutant transport.
🎯 Super Acronyms
M.I.N.D.
- Mass balance
- Inflow and Outflow
- Net change
- Dimension—the essentials in box modeling.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Box Model
Definition:
A simplified representation of a physical system used to visualize the transport and fate of pollutants within defined 'boxes' or volumes.
-
Term: Mass Balance
Definition:
An accounting method for substances entering and leaving a defined system, crucial for understanding pollutant concentration changes.
-
Term: Flux
Definition:
The rate of flow of a property per unit area, essential for modeling pollutant transport.
-
Term: Mixing Height
Definition:
The vertical extent in the atmosphere where pollutants are assumed to be well mixed, influencing air quality assessments.
-
Term: Convection
Definition:
The process of heat and substance transfer due to density differences in fluids, promoting mixing.
-
Term: Boundary Layer
Definition:
A layer of fluid in the vicinity of a bounding surface where effects of viscosity are significant, influencing pollutant redistribution.
-
Term: Pollutants
Definition:
Substances that contaminate the environment, affecting air and water quality.