Environmental Quality: Monitoring and Analysis
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basics of Fick's Law of Diffusion
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we're going to discuss Fick's Law of Diffusion. Can anyone tell me what this law describes?

It describes how substances move from high concentration to low concentration.

Great! Yes, we often summarize this movement with the formula: $$J_A = -D \frac{\partial C_A}{\partial z}$$. Why do you think there's a negative sign?

It means the flux moves against the concentration gradient?

Exactly! The negative sign indicates the directionality of the flux. Now, do you remember what the diffusion coefficient, D, signifies?

It indicates how easily a substance diffuses through a medium?

Spot on! D varies based on several factors. Let's delve deeper into those next.
Factors Affecting Diffusion
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, what are some factors that influence the diffusion coefficient, D?

I think the density of the medium matters.

Correct! Less dense mediums, like air, allow for greater diffusion compared to denser ones like water. Can anyone else think of other factors?

Temperature! Higher temperatures increase molecular motion.

Yes, that's right! Higher temperatures mean molecules have more energy to move. Lastly, how do molecular size and weight affect diffusion?

Smaller molecules diffuse faster than larger ones due to less resistance.

Exactly! Remember: less resistance means more diffusion. Keep this in mind when analyzing pollutants.
Applications in Environmental Monitoring
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about how we apply these diffusion principles in environmental monitoring. Can anyone provide an example?

Contamination in water bodies!

Exactly! When pollutants like sediments enter water, what factors should we consider to track their movement?

We should look at the concentration gradient between the sediment and the water.

Correct! We perform a mass balance with our equations. If I say rate in equals rate out, what does that imply?

It suggests a steady state in the system.

Spot on! It's crucial to monitor these dynamics for effective environmental management.
Flux and Mass Transfer Resistance
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's discuss flux and how it relates to different interfaces, such as sediment-water or air-water interfaces. How might these differ?

The factors affecting mass transfer would differ between water and air.

Correct! And what about the resistance involved?

If water is static, there’s more resistance, whereas moving water reduces resistance.

Exactly! Introducing convection can lower the resistance, enhancing the transfer rate. Remember the balance between convection and diffusion.

So more fluid movement means better pollutant transfer… I get it now!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, key concepts such as Fick's law of diffusion, the factors affecting the diffusion coefficient, and the relationship between concentration gradients and mass transfer resistance are discussed. The significance of understanding these principles is emphasized, particularly regarding environmental pollutant monitoring and analysis.
Detailed
Environmental Quality: Monitoring and Analysis
This section delves into the complexities of interphase mass transfer, vital for comprehending environmental quality monitoring. Key principles covered include Fick’s law of diffusion, which describes the relationship between flux and concentration gradients, and introduces the diffusion coefficient, D.
Fick's Law of Diffusion
The law demonstrates how concentration gradients drive the movement of substances, with flux (A) defined by the equation:
$$
J_A = -D \frac{\partial C_A}{\partial z}
$$
The negative sign indicates that flux moves from high to low concentration, presenting a critical perspective on mass transfer and resistance.
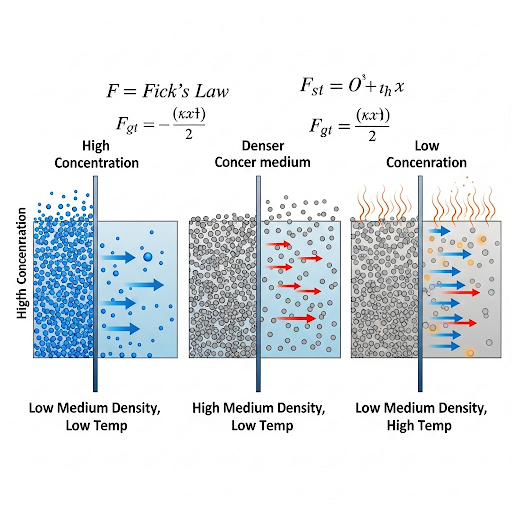
Factors Affecting Diffusion Coefficient
Understanding what affects the diffusion coefficient (D) is essential:
- Medium Density: Diffusion is generally greater in less dense mediums, e.g., in air compared to water, due to reduced resistance.
- Temperature: Increased temperature enhances molecular motion and energy, facilitating diffusion.
- Molecular Size: Smaller molecules tend to diffuse more readily than larger ones due to lower resistance encountered in mediums.
Environmental Applications**
The section introduces practical applications of these principles in environmental contexts, such as the modeling of pollutant movement in soil and water systems. Concepts such as mass balance, flux, and sediment interaction with water help illustrate these applications effectively. Understanding these principles is critical for monitoring and analyzing environmental quality and contamination events.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Flux and Mass Transfer Resistance
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, the term jA, we had discussed that this is defined by Fick’s law of diffusion.
This is very well studied, but it has the same form as what we had discussed last classes, potential difference versus resistance. So, in this, this is a system that we are talking about. This is z, this z is in this direction, So, there is movement that is happening of chemical that is going somewhere okay.
Now, the signage is like this. You see this is negative sign. The negative sign is an indicator of the direction of the flux, so this depends on how you are defining the frame of reference of this thing, okay.
Detailed Explanation
In this chunk, we are introduced to the term 'flux' as defined by Fick's law of diffusion. Flux refers to the rate at which particles pass through a specified area. In this case, the direction of flux is indicated by a negative sign, which denotes the direction of movement from areas of high concentration to areas of low concentration. The frame of reference is crucial as it affects how we interpret the movement of chemicals through different mediums.
Examples & Analogies
Think of a crowded room. If people are all clustered together, moving towards the exits, this is akin to high concentration moving to low concentration. The negative sign indicates that as people (or chemicals) move, they are relocating from a high-density area to a low-density area (akin to moving from the crowded space to the less crowded exit).
Factors Affecting Diffusion Coefficient
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So as we discussed D is the diffusion coefficient is the proportionality constant for most part, Ai preliminary things, but now people have figured out what the DA diffusion coefficient, what is it a function of? So, in the last class when we discussed, we looked at DA1 is greater than DA2, which means that diffusion of A in air is greater than diffusion of A in water because there is less resistance in air.
Detailed Explanation
The diffusion coefficient (D) is a key factor in understanding how substances move through different mediums. It is influenced by various factors such as the properties of the medium (e.g., air has less resistance than water, hence diffusion occurs faster in air) and the temperature (as temperature increases, particles move quicker, enhancing diffusion). Additionally, the size of the molecules also plays a role: smaller molecules generally diffuse faster than larger ones due to lesser resistance.
Examples & Analogies
Consider trying to move through a crowd versus moving through an open corridor. You can get through the corridor (like air) much faster than through a packed crowd (like water). Similarly, tiny balls will roll through sand (larger resistance) much more slowly than through grass (less resistance).
Mass Transfer in Environmental Systems
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us say we are interested in a pollutant, let us say it is sediment, easy system for us to understand, and there is a concentration. There is a region where this is contaminated and now this is in reference to our box model. There is a river and so there is a height of the water and there will be also a width of the water. There is a certain length where the contamination has happened.
Detailed Explanation
In environmental monitoring, understanding how pollutants, such as sediments, affect water quality requires modeling the contaminant's behavior in a defined area. The 'box model' simplifies this system by treating the contaminated section of a river as a well-mixed volume. It allows us to study how pollutants enter and exit this zone, providing insights into their impact on overall water quality.
Examples & Analogies
Imagine you have a fish tank and you add a drop of food coloring to one corner. Over time, the coloring spreads throughout the tank, but the way it mixes can be modeled just like pollutants in a river. Observing how the color diffuses can help you understand how pollutants might behave in real waterways.
Mass Balance Equation for Contaminants
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So here we need to know what is the rate of A transfer from sediment. This becomes a term in the mass balance in the balance. So, the overall mass balance we will write this rate in equals rate out, there is no accumulation, let us assume there is no accumulation at this time, steady state.
Detailed Explanation
In pollution modeling, the 'mass balance' concept is crucial. It states that the rate of a substance entering a space (like a river) must equal the rate of that substance exiting the space, assuming no changes in total quantity occur over time. This principle allows environmental scientists to determine the rates at which pollutants move into and out of different compartments, such as sediments and the water column.
Examples & Analogies
Think of a bathtub with the water flowing in at a constant rate and draining out at the same rate. If no water is added or removed while the inflow and outflow rates are equal, the water level stays the same. Similarly, in environmental systems, when pollutants enter and leave at the same rate, concentrations remain stable.
Understanding Interfacial Mass Transfer
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, we look at the interface transfer, so this has to be, we are saying rate of transfer, it has to be some combination of velocity and a concentration. The rate usually we will explain as flux into area, yeah. We already defined the flux...
Detailed Explanation
Interfacial mass transfer pertains to how substances move between different phases, such as from sediment to water. The rate of transfer (flux) is influenced by the velocity of the fluid and the concentration gradient, meaning that higher fluid velocity or larger concentration differences will enhance the transfer rate. This principle is essential in predicting how quickly pollutants can move from sediment into the water column.
Examples & Analogies
Visualize pouring syrup over ice cream. If you pour it slowly (low velocity), the syrup spreads out more gradually, while if you pour it rapidly (high velocity), it spreads quickly. Similarly, pollutants can move from sediments to water more quickly with increased water movement or higher concentration differences.
Key Concepts
-
Flux: The rate of transfer per unit area.
-
Concentration Gradient: It drives passive diffusion between regions.
-
Mass Transfer Resistance: It depends on both diffusion and convection.
-
Diffusion Coefficient: Determines how easily substances diffuse in a given medium.
Examples & Applications
Example 1: The rate of pollutants entering a body of water can be modeled using the principles of Fick's Law.
Example 2: The diffusion of a gas in air is influenced by its molecular weight and temperature.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
From high to low they do flow, diffusing gently, nice and slow.
Stories
Imagine a crowded beach where people are staying in clusters. As it becomes less crowded in certain areas, people begin to spread out towards quieter spots — this is similar to diffusion.
Memory Tools
D.C.M.V: Diffusion Coefficient, Medium Density, Viscosity — factors affecting diffusion.
Acronyms
DAMP
Density
Area
Molecular Weight
and Temperature — key factors influencing diffusion.
Flash Cards
Glossary
- Fick's Law of Diffusion
A principle that describes how substances move from regions of high concentration to regions of low concentration.
- Diffusion Coefficient (D)
A constant that indicates how easily a substance can diffuse through a medium.
- Flux (J_A)
The rate of transfer of particles per unit area per unit time.
- Concentration Gradient
The difference in concentration of a substance between two regions.
- Mass Transfer Resistance
The hindrance to the movement of particles across a phase interface.
Reference links
Supplementary resources to enhance your learning experience.
