Key Concepts
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Fick's Law of Diffusion
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to talk about Fick's Law of Diffusion. This law defines how substances move from areas of higher concentration to lower concentration. Can anyone explain what the equation looks like?

Is it jA = -DA (∂C/∂z)?

Great! This negative sign indicates the direction of flux. Remember, flux is how much substance is moving, measured over an area. Can someone tell me why this negative sign is important?

It shows that diffusion happens from high to low concentration.

Exactly! To remember this, think of 'flux flows down'. Now, let’s discuss the factors affecting the diffusion coefficient.
Factors Affecting Diffusion
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

The diffusion coefficient, DA, is influenced by several factors. Can someone name one?

Density of the medium?

Correct! Lower density allows for greater diffusion because there’s less resistance. How about temperature?

Higher temperatures increase diffusion because molecules move faster.

Well done! Another important factor is the size of the molecule. Why might smaller molecules diffuse more easily?

Because they can navigate through the medium without hitting as many obstacles.

Exactly! Let’s summarize: Lower density, higher temperature, and smaller sizes all lead to higher diffusion rates.
Mass Transfer in Environmental Systems
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s apply what we’ve learned to an environmental example. If we have polluted water near sediment, how do we assess the transfer of contaminants?

We can use a mass balance equation to see how much contaminant is coming from the sediment.

Exactly! The mass balance would include the inflow from sediment and outflow from the water. If the system is steady, what can we say about the mass rates?

The rate in equals rate out.

Right again! Ensuring we understand these concepts helps us manage water quality effectively. Let’s consider resistance in mass transfer next.
Evaluating Resistance in Mass Transfer
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

When assessing mass transfer, we must look at resistance. Can anyone explain how convection influences resistance?

Adding convection reduces resistance because it enhances the flow and mixing.

Correct! Thus, higher velocities in water can significantly impact how efficiently pollutants diffuse. Let's remember: 'More flow, less woe'.

So, if there is no convection and only diffusion, the resistance would be quite high?

Exactly! And that’s why understanding the hydrodynamics of the system is critical for calculating mass transfer.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section elaborates on Fick's law of diffusion and its application in understanding interphase mass transfer. It details the factors affecting diffusion coefficients, resistance in mass transfer, and the implications for environmental systems, including pollutants in water and sediment.
Detailed
Detailed Summary
This section delves into the key concepts of interphase mass transfer, focusing primarily on flux and mass transfer resistance as governed by Fick’s laws of diffusion.
Key Points:
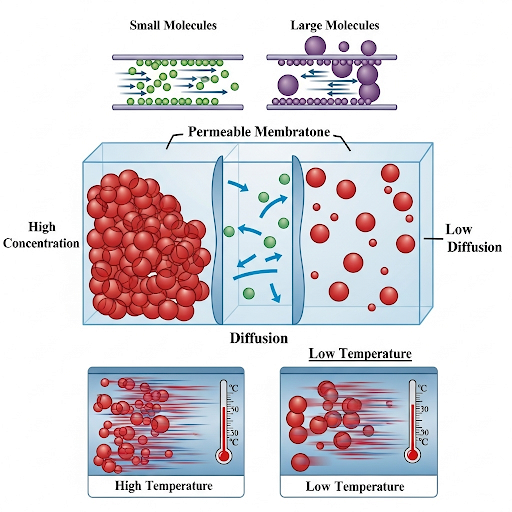
- Fick's Law of Diffusion: The equation, jA = -DA (∂C/∂z), illustrates that diffusion occurs from regions of higher concentration to lower concentration, where DA is the diffusion coefficient. The negative sign indicates the direction of flux.
- Factors Affecting Diffusion Coefficient (DA): Several factors influence the diffusion coefficient, including:
- Density of the Medium: Lower density allows for greater diffusion.
- Temperature: Higher temperature increases molecular kinetic energy, facilitating diffusion.
- Molecular Size: Smaller molecules diffuse easier than larger ones, encountering less resistance.
- Viscosity: Greater viscosity results in increased resistance to diffusion.
- Mass Transfer in Environmental Systems: In environmental contexts, such as assessing pollutant movement from sediments to water bodies, it's crucial to account for the rate of A transfer. Mass balance equations help in evaluating these interactions and understanding concentration changes in static and moving fluids.
- Resistance & Convection: Resistance to mass transfer changes based on the physical conditions—convection vs. diffusion plays a significant role in determining mass transfer rates. Higher flow velocities reduce resistance, requiring an evaluation of hydrodynamic conditions in water systems.
This understanding of interphase mass transfer mechanisms is vital for effective environmental monitoring and management.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fick's Law of Diffusion
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, the term jA, we had discussed that this is defined by Fick’s law of diffusion. This is very well studied, but it has the same form as what we had discussed last classes, potential difference versus resistance.
Detailed Explanation
Fick's law of diffusion explains how substances move from areas of high concentration to areas of low concentration, which is a fundamental concept in understanding mass transfer. Essentially, it details the 'flux' or flow of a substance, which can be affected by various factors in the environment. The law states that the rate of transfer (flux) is proportional to the concentration gradient, meaning that the greater the difference in concentration, the faster diffusion happens.
Examples & Analogies
Think of a drop of food coloring in water. Initially, the color is concentrated in one spot, but over time, it spreads throughout the water. This movement from a concentrated area (high concentration) to a more diluted area (low concentration) illustrates Fick's law in action, showing how diffusion works in a fluid medium.
Significance of Negative Flux
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The negative sign is an indicator of the direction of the flux, so this depends on how you are defining the frame of reference.
Detailed Explanation
In many equations regarding flux, the negative sign indicates that particles are moving from a region of higher concentration to lower concentration. This is important because it highlights that flux is directional; changes in the defined reference frame can affect our calculations, hence the need for clarity in definitions. When we indicate flux as positive, we typically refer to the movement in the direction of decreasing concentration.
Examples & Analogies
Imagine a hill where balls are placed at the top and allowed to roll down. The flow of the balls from the top to the bottom is analogous to the negative flux, as they are moving from a high elevation (high potential) to a low elevation (low potential). This direction of movement is indicative of how concentrations equilibrate in physical systems.
Factors Influencing Diffusion Coefficient
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
As we discussed D is the diffusion coefficient which is the proportionality constant for most part; but now people have figured out what the DA diffusion coefficient is a function of.
Detailed Explanation
The diffusion coefficient (D) is significant as it quantifies how quickly substances diffuse in different environments. It depends on factors such as the medium's density, temperature, molecular weight, and viscosity. For instance, lighter substances tend to diffuse more easily. As temperature increases, molecules move faster, impacting the diffusion rate positively, and larger molecules often face more resistance, decreasing diffusion efficiency.
Examples & Analogies
Consider how perfume spreads in a room. If the air is warm (high temperature), the scent spreads quickly due to the increased energy of air molecules. However, if you used a thick syrup instead of air, the diffusion would happen much slower because the syrup's higher viscosity creates more resistance. This illustrates how diffusion can be influenced by various properties of the medium.
Mass Transfer in Environmental Systems
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us say we are interested in a pollutant, let us say it is sediment, easy system for us to understand, and there is a concentration.
Detailed Explanation
In environmental systems, understanding mass transfer is crucial for assessing the impact of pollutants like sediments on water quality. The key focus is on how pollutants transition from contaminated sources to other areas, affecting overall quality. Using models like box or plug flow models allows researchers to analyze these systems by simplifying complex interactions into comprehensible equations that represent mass balance equations.
Examples & Analogies
Think about a sponge in a bucket of water. If the sponge is dirty and placed in clean water, pollutants from the sponge will slowly transfer to the water. By observing how the concentration of pollutants changes in water over time, scientists can study the transfer rate and ultimately determine the water's quality. This sponge example is similar to how real-world sediment might affect water systems.
Resistance and Mass Transfer Rate
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The rate usually we will explain as flux into area, we have already defined the flux.
Detailed Explanation
The mass transfer rate is influenced significantly by resistance, which varies depending on factors such as diffusion and convection currents. If fluid is stagnant, resistance is high, but if there's movement, resistance decreases, enhancing the mass transfer rate. Understanding this relationship is vital for managing how substances disperse in various media, particularly related to contaminants in environmental science.
Examples & Analogies
Imagine trying to push a beach ball through water. If the water is still, it’s harder to move the ball (high resistance). But if someone is actively stirring the water, the ball moves more easily (lower resistance). This demonstrates how movement can facilitate mass transfer by otherwise impeding it in static conditions.
Key Concepts
-
Fick's Law of Diffusion: Describes how substances move from high to low concentrations.
-
Diffusion Coefficient (DA): Influences the rate of diffusion, dependent on factors such as density and temperature.
-
Mass Transfer Resistance: Affects how pollutants move in environmental systems, significant in assessing water quality.
Examples & Applications
An instance of higher diffusion rate in air compared to water due to lower viscosity.
Calculating the mass balance of pollutants in a river affected by sediment contamination.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
'Flux flows down, concentration is king, higher to lower, is the diffusion swing.'
Stories
Once in a crowded festival, small balloons floated easily among people, while big ones struggled. This represents how smaller molecules diffuse better than larger ones.
Memory Tools
To remember the factors affecting DA, use: 'Dancing Turtles Move Vigorously': Density, Temperature, Molecular size, Viscosity.
Acronyms
Remember 'DAMP' for factors affecting diffusion
Density
Accumulation
Molecular size
Temperature.
Flash Cards
Glossary
- Fick's Law
A principle governing diffusion, indicating that flux occurs from high to low concentration.
- Diffusion Coefficient (DA)
A measure of how easily molecules diffuse through a medium, influenced by factors like density and temperature.
- Flux
The rate at which a substance moves through a surface area.
- Mass Transfer Resistance
The opposition encountered by a substance moving from one phase to another, affected by diffusion and convection.
- Hydrodynamics
The study of fluids in motion, affecting how they interact with contaminants in environmental systems.
Reference links
Supplementary resources to enhance your learning experience.
