Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Transfer Coefficients
Unlock Audio Lesson
Let's start by discussing what mass transfer coefficients are and why they are important in environmental quality monitoring. Can anyone tell me what influences these coefficients?
Is it related to the properties of the medium, like air and water?
Correct! The coefficients vary based on properties like air and water density, viscosity, and diffusion coefficients. It’s crucial to choose the appropriate correlation for each scenario.
What happens if we use the wrong correlation?
Using the wrong correlation can lead to inaccurate estimates of pollutant concentrations, affecting environmental assessments.
So, how do we derive these coefficients?
We can obtain them from literature or specific handbooks that provide various correlations based on empirical data from different situations. Remember to note them down!
Understanding Evaporation Dynamics
Unlock Audio Lesson
Next, let's discuss evaporation. Can anyone tell me the main driving forces for evaporation?
The concentration of the pollutant, temperature, and wind speed, right?
Exactly! These factors can significantly affect how quickly a substance evaporates.
What if we have a chemical spill? How does that change our calculations?
Great question! A chemical spill introduces immediate risks, and understanding the rate of evaporation becomes critical. We often need to assess the concentration in the air and its potential impact on health.
Can we predict how long it will take for a substance to reach harmful concentrations in the air?
Yes! By setting up and solving the appropriate differential equations, we can model this situation effectively.
Mathematical Modeling in Emergency Response
Unlock Audio Lesson
Now, let’s explore how these models contribute to emergency responses. Why do we need to simulate worst-case scenarios?
To prepare for potential disasters and ensure public safety?
Exactly! Understanding the worst-case scenario can guide us in planning the necessary response measures effectively.
What types of situations are we preparing for?
Spills on land or water, and even laboratory accidents. Each scenario involves different calculations and assumptions.
How can we assure the response model takes into account environmental changes?
We adjust our models for the conditions of the day, such as wind speed and stability. This ensures our calculations are as accurate as possible.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, various aspects of environmental quality monitoring are examined, emphasizing the calculations related to evaporation from different surfaces. The derivation of mass transfer coefficients and the impact of environmental conditions on these calculations are discussed alongside the importance of choosing the correct correlation for specific scenarios.
Detailed
In this section, we delve into the intricacies of environmental quality monitoring and analysis. The discussion begins with the derivation of mass transfer coefficients related to evaporation from different surfaces, including lakes, rivers, and oceans. Several correlations exist to estimate these coefficients, influenced by environmental parameters such as water velocity, air velocity, temperature, and diffusion coefficients. Students are guided to select appropriate correlations based on specific scenarios.
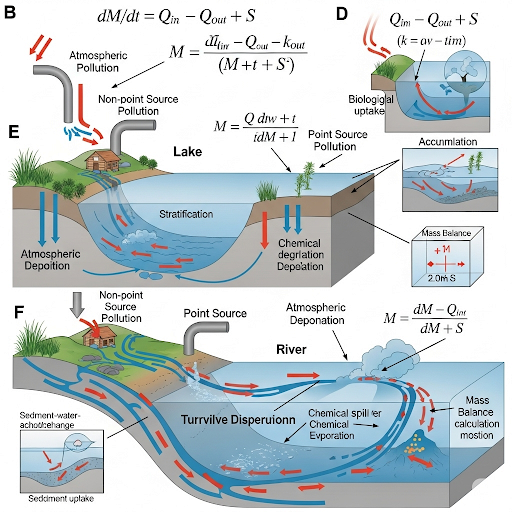
The significance of understanding the concentration of pollutants over time is highlighted through the formulation of differential equations that represent mass balance. An emphasis is placed on how environmental incidents, such as chemical spills, can be modeled to predict concentration changes in various mediums, thus underscoring the relevance of these calculations in emergency response scenarios. Through examples, the section explores how mathematical models can aid in assessing the risks posed to human and ecological health from environmental contaminants.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Transfer Coefficients and Correlations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we have KA2.
= +
1 1 2 2
2 2 1
We derived this. So, now, this is the next step. Now, we have the driving force in place we know that, this is the next step. So, this you have to calculate, n is constant it is already known, should be known for the chemical you are looking at. The mass transfer coefficients kA12 and kA21 are to be obtained from correlation. So, there are a variety of correlations that are available in literature.
Detailed Explanation
In this chunk, we are introduced to the concept of mass transfer coefficients (kA12 and kA21) which are essential for calculating the rate of mass transfer in environmental processes. These coefficients need to be obtained from established correlations found in literature, which have been developed through experimental observations under different environmental scenarios. It's crucial to select the appropriate correlation based on the specific environment being studied, such as lakes, rivers, or oceans.
Examples & Analogies
Imagine trying to pour a drink from a bottle. The speed at which the drink flows out depends on how wide the bottle's opening is and how high you hold it. The wider the opening and the higher the bottle, the faster the drink flows. In environmental science, the mass transfer coefficients work similarly—they determine how quickly substances can move from one state to another, influenced by conditions like temperature, density, and flow velocity.
Estimating the Overall Coefficient
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Once you do that, you go back to the calculate, estimate 2KA or 1KA, the overall coefficient. Now we go back to the main equation, 1 2 the overall coefficient. Now we go back to the main equation.
Detailed Explanation
After obtaining the mass transfer coefficients, the next step is to estimate the overall mass transfer coefficient (KA). This is crucial for solving the main differential equation that describes the mass balance of the chemical in question. The process involves substituting the known values into the equation to find the concentration of the chemical over time, establishing how it changes as mass is transferred out of the system.
Examples & Analogies
Think of baking a cake—once you've gathered all your ingredients (the mass transfer coefficients), you need to mix them properly (estimate the overall coefficient) to achieve the right texture and flavor. The overall mass transfer coefficient is like the baking process, where the ingredients come together to create the final product—the concentration of the chemical in the environmental context.
Understanding Differential Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This becomes our problem now. This is our differential equation, we know this term now, we have estimated this term, this is a function of time. Because this is changing, this is a finite problem, so it will change.
Detailed Explanation
In this chunk, we start to discuss the differential equation that arises from the mass balance calculations. This equation represents how the concentration of the chemical changes over time, emphasizing that this is a dynamic process influenced by the driving forces of mass transfer. Understanding this equation is fundamental for predicting how pollutants dissipate in the environment over a given timeframe.
Examples & Analogies
Consider a bathtub filling up with water—if you turn on the faucet (the driving force), the water level rises. However, if you also have a drain open (loss of mass), the level rises more slowly. The differential equation describes this balance: how fast the water level rises is determined by the inflow minus the outflow, similar to how the concentration of a pollutant changes over time.
Initial Conditions and Integration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, this initial condition has to be determined. So you say finite amount of chemical was dumped into the volume. Say if M 0 was dumped A into the volume, this divided by the volume of lake should be the initial concentration.
Detailed Explanation
To solve the differential equation accurately, we need to specify an initial condition, which is the concentration of the chemical at the beginning of our observation (time t=0). This is crucial because it serves as the baseline from which all future concentrations are calculated. For example, if a specific mass of a chemical is released into a body of water, we need to determine its initial concentration to analyze how it will change over time.
Examples & Analogies
Think of starting a race—if everyone begins at different starting lines (initial conditions), it affects who finishes first. Similarly, in environmental analysis, knowing the initial concentration of a pollutant defines how we track its dispersion and degradation over time, much like how starting positions affect race outcomes.
Using the Equation for Practical Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is a very simple, this is like a reaction, first order reaction. This is like a first order reaction equation. So, we have this term here or this term here, we are seeing that the rate is the first order term, evaporation is the first order of term.
Detailed Explanation
The discussion leads towards characterizing the process as a first-order reaction, where the rate of mass transfer is proportional to the concentration. This simplifies the modeling of the chemical's behavior in the environment, allowing us to predict how quickly it will evaporate or degrade. Understanding this first-order relationship is fundamental in environmental science for assessing risks and remediation efforts.
Examples & Analogies
Imagine a candle burning down—initially, it burns quickly because there's plenty of wax (high concentration), but as it gets lower, it takes longer to burn the remaining wax (decreasing concentration). Similarly, in our pollution scenario, the rate of evaporation slows as concentration decreases, and modeling this first-order reaction helps us predict the time until the pollutant is negligible.
Dispersion and Environmental Concerns
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Suppose there is a big spill in a lake, somebody has, there was an accident...
Detailed Explanation
This segment discusses practical scenarios such as pollutant spills in water bodies. Here, the environmental concerns are raised, emphasizing the need to calculate how contaminants migrate through water and potentially into the atmosphere. Understanding dispersion dynamics is vital for assessing risks to aquatic life and human health, exemplifying the importance of the previous mathematical models in real-world applications.
Examples & Analogies
Consider a dropped bottle of ink on a clean white paper—initially, it looks stark, but if you add water or the paper absorbs it, the ink spreads out. Similarly, in the case of a chemical spill in a lake, we must consider how quickly and extensively the chemical will spread, affecting nearby ecosystems and water quality.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Transfer Coefficient: A measure of the rate at which a substance moves from one phase to another.
-
Evaporation Dynamics: Key factors that influence evaporation rates, including temperature, airflow, and concentration.
-
Differential Equations: Mathematical formulations that describe how quantities change over time, essential for modeling concentrations.
-
Emergency Response: The application of models to predict and respond to chemical spills and environmental emergencies.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using correlation data to estimate the mass transfer coefficient for evaporation in a lake environment.
-
Modeling the concentration of a chemical spill on a road to assess environmental risk over time.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the air, evap’rate fair, wind and warmth help it to share.
📖 Fascinating Stories
-
Imagine a lake where the sun's rays warm the water, causing it to turn to vapor. Fishermen worry about what pollutants might swim away with it.
🧠 Other Memory Gems
-
EVAP = Evaporation Visibility & Air Pressure; understand the key factors in evaporation.
🎯 Super Acronyms
MTC = Mass Transfer Coefficient = Maximizing Transport Communication.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Transfer Coefficient
Definition:
A parameter that quantifies the mass transfer rate between phases, impacted by concentration gradients.
-
Term: Evaporation
Definition:
The process by which liquids turn into vapor, influenced by factors such as temperature and environmental conditions.
-
Term: Differential Equation
Definition:
An equation that relates a function with its derivatives, often used to describe changing quantities over time.
-
Term: Concentration
Definition:
The amount of a substance in a given volume, crucial for assessing environmental pollutant impacts.
-
Term: Chemical Spill
Definition:
An accidental release of a harmful chemical into the environment, requiring immediate assessment and response.