Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Contaminant Transport
Unlock Audio Lesson
Today, we'll discuss how contaminants move through sediments. Can anyone tell me what we mean by contaminant transport?
Is it how pollutants move from one area to another within the soil or sediment?
Exactly! It's all about how these substances migrate. One of the key concepts is the 'general domain equation.' This helps us model the concentration of contaminants in sediment over time. Can anyone remember if we discussed a specific factor that affects how fast these contaminants move?
The retardation factor, right?
Correct! The retardation factor indicates how contaminants slow down as they move through particles in the sediment.
Why is that important?
It's crucial for accurately modeling contaminant behavior, especially in environmental assessments.
So, does that mean contaminants will take longer to reach groundwater?
Yes! Now let's dive into boundary conditions that help us define how we model these systems.
Boundary Conditions in Sediment Transport
Unlock Audio Lesson
When we model transport, boundary conditions are essential. For instance, what happens at the sediment-water interface?
Is it where the contaminant leaves the sediment and enters the water?
That's right! This is referred to as a flux boundary condition because it measures how much contaminant passes through that boundary per unit time.
What formulas do we use to describe that?
Great question! We often use concentration values and terms from our general equation. Are you familiar with the semi-infinite boundary concept?
Yes, it means there's a point far from the edge where concentrations can be considered constant over time?
Exactly! In many cases, this helps simplify our calculations. Let's make sure we understand these concepts before moving on.
Estimating Flux and Concentrations
Unlock Audio Lesson
To assess sediment quality, we need to measure flux and concentrations. How do you think we can extract data from sediment samples?
I remember we talked about core sampling last time!
Right! Core sampling allows us to capture a column of sediment and assess the concentration at various depths effectively.
What method do we use once we have the sediment sample?
Typically, we use solvent extraction methods. Can anyone share how that might affect our concentration readings?
If we extract both liquid and solid phases, it might skew our reported values, right?
Exactly! Always remember to clarify what phase you're reporting and what that means for interpreting your results.
Modeling Concentration Profiles
Unlock Audio Lesson
Now that we understand flux and measurement, let's talk about modeling concentration profiles. What happens to concentrations over time?
They will likely change as contaminants move deeper into the sediment, right?
Exactly! Initially, higher concentrations are at the surface, but as time progresses, deeper layers may show increases depending on diffusion and other factors.
Are there scenarios where concentrations might not be uniform?
Absolutely! Variability can occur with soil composition, layer behavior, and even seasonal changes in water movement.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concept of contaminant transport within sediment environments is explored. This involves understanding the general domain equations governing transport, how to apply boundary conditions, and the significance of retardation factors in sediment dynamics.
Detailed
Detailed Summary
In this section, Prof. Ravi Krishna presents an in-depth analysis of contaminant transport through sediments, which is critical for evaluating environmental quality. Key concepts include:
- General Domain Equation: The section begins by outlining the general domain equation that governs transport phenomena, particularly when examining a vertical sediment layer. This equation helps describe the mathematical relationships governing the concentration of contaminants.
- Retardation Factor: Central to understanding contaminant behavior in sediments, the retardation factor, denoted as (D + E * k*), indicates how contaminants are slowed down as they migrate through sediment.
- Boundary Conditions: The importance of applying accurate boundary conditions—specifically flux boundary conditions at the sediment-water interface (z = 0) and semi-infinite boundary conditions at z = ∞—is discussed. These conditions allow for the modeling of contaminant flux into and out of the sediment.
- Analytical Solutions: The challenges of obtaining analytical solutions for different dimensional transport models are highlighted, paving the way for numerical solutions in practical scenarios. Laplace transforms are suggested as a technique for solving the transport equations.
-
Measurement and Monitoring: A particular focus is placed on the practical aspects of sediment sampling to monitor chemical concentrations, emphasizing core sampling and the extraction techniques used to assess sediment quality. The dynamics of sediment concentration profiles are discussed, reflecting how initial contaminant concentrations change over time due to transport processes.
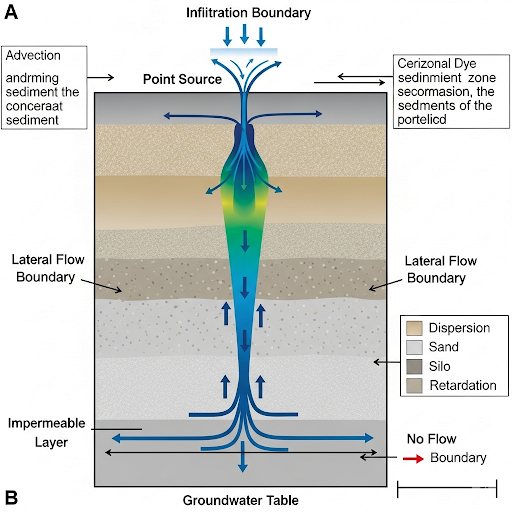
Through these points, this section lays a robust theoretical framework for understanding sediment contamination and its implications for environmental monitoring.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Contaminant Transport Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Yesterday we were discussing the contaminate transport. So, we were looking at the development of the transport model within a system here, so we are looking at transport in this z direction. So, the equation we derived yesterday is:
$
\frac{\partial C}{\partial t} = D \nabla^2 C
$
This is called as general domain equation or the process that is happening in the domain. The sediment is the domain, the process is happening. This describes the processes happening here.
Detailed Explanation
In this portion, we are introduced to the concept of contaminant transport within sediments. The focus is on how substances move within a specific area, which in this case is the sediment, and how we describe these movements mathematically using the general domain equation. The 'z direction' refers to how we consider movement vertically within the sediment layers, where the transport of contaminants can be modeled over time.
Examples & Analogies
Imagine a sponge soaking up water. As the sponge absorbs more water, it becomes saturated, and the water can also move out in certain directions. Similarly, in sediment, contaminants can be absorbed and diffused, illustrating how particles behave in a porous medium.
Understanding the Retardation Factor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This term here, (D + E . R*) is called as the Retardation Factor, so we have defined it as R. This retardation of A between 3 and 2, which means that this equation describes what is happening in the bulk of the sediment of the domain that is why we call it as a domain equation.
Detailed Explanation
The Retardation Factor is crucial for understanding how the movement of contaminants within sediments is slowed down compared to their movement in the water. It accounts for the interactions between contaminants and sediment particles. In this case, A refers to the quantity of substance we are observing, and the factors in the equation represent the different forces and interactions taking place.
Examples & Analogies
Think of traffic on a busy road. Vehicles can move freely when there are no obstacles, but if there are traffic lights or construction zones, their speed is affected. Similarly, the Retardation Factor slows down the movement of contaminants as they navigate through sediment, which acts like these obstacles.
Boundary Conditions in Transport Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now here, we need the 2 boundary conditions and one initial condition to solve this. So, our domain starts here. This is z = 0 and it goes down, this is how we have defined our system. One has to look at what is happening and usually boundary conditions are written at a particular location at all time greater than 0.
Detailed Explanation
Boundary conditions are important constraints used in mathematical models to define how the system behaves at its edges or limits (boundaries). In this discussion, z = 0 represents the surface level of the sediment, which is critical for setting the conditions regarding how contaminants enter or exit the system. Essentially, these conditions help determine what happens at the start of our model and how we can analyze the contaminant transport over time.
Examples & Analogies
Imagine a bathtub filled with water. The edge of the tub is like our boundary condition – no water can overflow if the conditions are set correctly. If we pour water in (contaminants), we need to know what happens to the water level (substance concentration) at the edge (boundary) of the tub for our model to be accurate.
Flux and Transport Mechanisms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Material is what is being brought from one side of the interface is leaving to the other side at the same rate; the rate at which it is brought in is going away. What is the rate at which material is brought to the interface? ... This is diffusion.
Detailed Explanation
In the context of transport within sediments, flux represents the rate at which contaminants are entering or leaving a particular area. This explanation highlights diffusion, a process where substances move from an area of higher concentration to an area of lower concentration. Understanding how flux works helps in predicting how pollutants disperse in the environment due to natural processes.
Examples & Analogies
Consider a drop of food coloring in a glass of water. Initially, the color is concentrated where it was dropped, but over time, the color spreads throughout the water due to diffusion. This represents how contaminants can move from areas of high concentration (sediment) to lower concentration (water).
Semi-Infinite Boundary Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, this finite distance again it is at all time greater than 0, it should be valid for all time greater than 0. ... This is called as a semi-infinite boundary condition. This is used a lot in this kind of transport problems, boundary condition, which assumes there is nothing called as infinity.
Detailed Explanation
A semi-infinite boundary condition is a concept used to simplify the calculations in a model by assuming that, at a great enough distance from the area of interest, there are no changes or effects from the area in question. This allows for easier mathematical treatment of the transport processes without needing to consider the full complexity of the physical space.
Examples & Analogies
If you throw a stone into a still pond, the ripples expand outward. Now, if you think about how far those ripples go, you can't see any changes at a certain distance. We consider that distance as 'infinity' because, beyond that point, the ripples no longer have a noticeable effect. This is similar to how we treat far areas in modeling transport in sediments.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
General Domain Equation: A mathematical representation describing contaminant concentrations.
-
Flux Boundary Condition: Condition defining contaminant flow at an interface.
-
Retardation: The factor that describes the slowdown of contaminants in sediments.
-
Core Sampling: Technique for sampling sediment to analyze concentration profiles.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For example, when modeling a contaminated sediment site, researchers may find that the concentrations at the sediment-water interface are significantly higher than those measured at depth.
-
In practice, when a core sample is taken, the data obtained can indicate a sharp decrease in contaminant concentration as one moves deeper into a sediment layer.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When contaminants roam and sediments flow, the retardation factor makes their speed slow.
📖 Fascinating Stories
-
Imagine a river with a heavy storm, pollutants rush, but some get conformed. Sediments hold fast, slowing their pace, determining how long till they reach the base.
🧠 Other Memory Gems
-
Remember 'C-B-F' for 'Core Sampling, Boundary conditions, Flux', essential for sediment transport analysis.
🎯 Super Acronyms
Use 'TRAC' for 'Transport, Retardation, Analysis, Concentration' to remember the key topics in sediment transport.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Contaminant Transport
Definition:
The movement of pollutants through soil or sediment, governed by various physical and chemical processes.
-
Term: Retardation Factor
Definition:
A parameter that describes how much slower a contaminant moves through sediment compared to the flow of water.
-
Term: Boundary Condition
Definition:
Conditions applied to a physical model that define how the model behaves at specific boundaries.
-
Term: Flux
Definition:
The rate of flow of a property per unit area, such as the concentration of contaminants passing through a boundary.
-
Term: Core Sampling
Definition:
A technique for collecting sediment samples in cylindrical shapes to analyze stratified concentrations.
-
Term: Semiinfinite Boundary Condition
Definition:
Assumption used in modeling where the distance from the region of interest is considered infinitely far, simplifying calculations about concentration.
-
Term: Laplace Transform
Definition:
Mathematical transformation used to simplify complex differential equations, often employed in solving transport models.