Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Kinematics
Unlock Audio Lesson
Today, we are diving into fluid kinematics. Understanding how fluids move relative to one another is crucial for solving many engineering problems. Can anyone tell me what fluid kinematics looks at?
Does it focus on the motion of fluids without considering the forces causing the motion?
Exactly, great point! We are more concerned with how fluid particles move and the patterns they create. One useful way to visualize these patterns is through the use of models like the Hele-Shaw apparatus.
What exactly is that apparatus, and how does it work?
The Hele-Shaw apparatus visualizes flow by observing the movement of fluid between two flat plates. It allows us to see streamlines, which illustrate how the fluid flows around obstructions.
Flow Visualization Techniques
Unlock Audio Lesson
Let’s discuss different flow visualization techniques. Why do you think visualizing flow is important?
To better understand how fluids behave in real-world scenarios?
Exactly! Videos and simulations can show phenomena like wake formation or vortex shedding, which can be fascinating. Has anyone seen videos of these phenomena?
I watched one where a cylinder caused a wake. It's interesting how it changes with the flow speed.
That’s a perfect example! Knowing how flow patterns change can guide engineering decisions in design.
Examples of Fluid Kinematic Problems
Unlock Audio Lesson
Let’s move on to practical examples. Who can tell me about irrotational velocity fields?
Isn’t that where the flow has no rotation and can be defined through potential functions?
Correct! Now, let’s find the irrotational velocity field based on specific potential functions. Can anyone provide an example?
What if we used the potential function phi equal to 3x + 2y?
Great choice! Now, how would we find the velocity components?
Using the Continuity Equation
Unlock Audio Lesson
Let’s talk about the continuity equation for incompressible flow. Who can state what it is?
It states that the sum of the partial derivatives of velocity components must equal zero?
Exactly! In a two-dimensional case, this condition helps us evaluate if our derived flow fields satisfy the incompressibility requirement.
Can we apply this to check our previous examples?
Yes! It’s essential for validating our findings. Let’s go back and verify.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section emphasizes solving fluid kinematics problems using techniques discussed in referenced textbooks, along with experimental setups like the Hele-Shaw apparatus. It covers key concepts such as irrotational flow, velocity fields, and conditions for incompressibility with examples of problem-solving methods.
Detailed
Problems Solving on Black Board
In the chapter on Fluid Mechanics, this section focuses on problem-solving in fluid kinematics, providing students with practical applications to enhance their understanding. The lecture, led by Prof. Subashisa Dutta, employs various reference texts, including those by Cengel, Cimbala, FM White, and Bidya Sagar Pani, to visualize fluid systems effectively. The importance of using the Hele-Shaw apparatus for demonstrating flow patterns is underscored, as it allows students to visualize streamline, pathline, and streakline patterns, despite any obstructions presented in a fluid's path.
The lecture discusses the significance of flow visualizations available on the internet, illustrating phenomena such as wake formation behind structures and vortex shedding in various flow scenarios, including unsteady patterns from oscillating plates. These resources enable students to gain a deeper understanding of fluid motion through observation.
Moreover, the section revisits essential concepts such as the definition of velocity fields, the relation of accelerations to velocity, and the conditions of fluid motion, emphasizing four types of motion and their related deformations. By the conclusion, the instructor provides a recap of irrotational velocity fields and continuity equations through solving various examples, guiding students step-by-step to enhance their problem-solving skills in fluid dynamics.
Youtube Videos
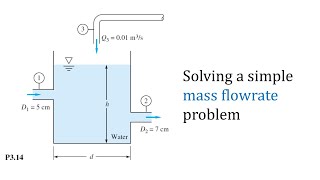
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid Kinematics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Very good afternoon to all of you. Today we are going to have fluid kinematics solving some of the problems on the blackboard. Looking that as I said it earliest we are again having same reference book starting from Cengel, Cimbala, F M White and Bidya Sagar Pani. So my sincere request to you to please look for the book of Cengel, Cimbala book which have which gives lot of illustrations to visualize the fluid flow problems because if would try to understand the fluid kinematics which is very interesting stuff subject.
Detailed Explanation
In this chunk, the professor introduces the topic of fluid kinematics and the method of solving associated problems. He emphasizes the importance of certain reference books, notably those by Cengel and Cimbala, which are filled with illustrations to help visualize fluid flow scenarios. The main goal is to engage students with fluid kinematics, a fascinating area of study in fluid mechanics.
Examples & Analogies
Think of fluid kinematics like learning to drive a car. You need guides (like books) to show you the rules of the road (fluid behavior). Just as a driving manual features diagrams to help you understand where to go and how to respond to various situations, the reference books highlighted give visual insights into fluid movement, making the subject easier to grasp.
Flow Visualization Techniques
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Beside this solving the problems also we should look at how the flow behavior flow visualizes a technique that is what is very good illustrations are there in Cengel, Cimbala book. So please refer to Cengel, Cimbala book of fluid mechanics and other 2 books as we refer earlier case also.
Detailed Explanation
The professor stresses the value of understanding how fluid behaves and visualizing flow patterns. He encourages students to refer to textbooks with good illustrations that enhance their understanding. Effective visualization techniques are key to mastering fluid mechanics concepts and help explain complex flow behaviors.
Examples & Analogies
Imagine you are trying to learn how to play a sport—say soccer. Watching videos of professional players helps you understand how to move with the ball and anticipate the game's flow. Similarly, in fluid mechanics, visualizing flow through illustrations helps us anticipate and understand the behavior of fluids.
Hele-Shaw Apparatus Explanation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Looking that again I will show it there it could be conduct a very small experiments which is called Heles apparatus. So where we can have an apparatus like these and we can create the streamline pattern, the streakline pattern and pathline patterns using these the small device which is called the Hele-Shaw apparatus.
Detailed Explanation
The professor introduces the Hele-Shaw apparatus, a tool used for conducting small experiments to visualize flow patterns such as streamlines, streaklines, and pathlines. This apparatus effectively demonstrates fluid flow and its behavior around obstructions, providing students a practical insight into the concepts they are studying.
Examples & Analogies
Using the Hele-Shaw apparatus is like using a clear plastic bottle filled with colored water to demonstrate how a ship's hull affects water flow. When you pour the water, you can see how the shape of the bottle creates different flow patterns, similar to how the Hele-Shaw apparatus shows the interactions between fluid and solid boundaries.
The Importance of Internet Flow Visualizations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And if you look it very interesting flow visualizations are available in internet. Please refer to look at these flow visualization details, videos what these are available in the internets.
Detailed Explanation
The professor highlights the availability of online resources for flow visualization, encouraging students to seek out videos that depict fluid behavior in various scenarios. These resources provide dynamic insights into concepts that might be hard to visualize through static illustrations alone.
Examples & Analogies
Consider how YouTube tutorials can teach you everything from cooking to playing a musical instrument. Seeing the process in action can clarify complex techniques. Similarly, online flow visualization videos show how fluid dynamics operate in real-time, contributing to a deeper understanding.
Advanced Flow Visualization Techniques
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These are details obtained from the CFD solutions. So we can get it from the CFD solutions these type of vortex patterns and very interesting vortex patterns and that is what it shows that how these the average velocity line changes with that and with a comparison with experimental data.
Detailed Explanation
In this section, the professor discusses advanced flow visualization techniques, focusing on computational fluid dynamics (CFD) solutions. These solutions allow for detailed representations of fluid behavior, such as vortex patterns, which can be compared with experimental data. Understanding these patterns is crucial in various engineering applications.
Examples & Analogies
Think of it like using a high-tech video game to understand physics. The game simulates various scenarios that help players see the outcome of their decisions. Similarly, CFD provides a digital environment where engineers can visualize how changes in design affect fluid dynamics before implementing them in real life.
Recap of Fluid Kinematics Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Before starting solving the blackboard applications, let me just have a recap that what we already discussed in the fluid kinematics is that you know that any velocity field we can define as 3 scalar components.
Detailed Explanation
The professor summarizes key concepts in fluid kinematics, such as defining velocity fields using three scalar components and the distinction between local and convective accelerations. Recapping these definitions ensures that students are on the same page before diving deeper into problem-solving.
Examples & Analogies
Just like before starting a group project, a team would recap what they learned in previous meetings to ensure everyone understands the main ideas, this summary ensures that all students are clear on previous discussions and ready to tackle new problems effectively.
Introduction to Initial Example Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us start the first example 1. Example 1 says that what is the irrotational velocity field associated with the potential functions as given here.
Detailed Explanation
The professor moves on to discussing specific examples, starting with the first problem involving irrotational velocity fields connected to potential functions. This kind of example serves to apply theoretical knowledge to practical scenarios, reinforcing learning.
Examples & Analogies
Think of starting a math problem set after reviewing key concepts. By tackling specific examples, like determining irrotational velocity, students get to practice the skills they've just learned, bridging theory and application.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Fields: Mathematical description of fluid motion, defined through components of velocity.
-
Continuity Equation: Reflects that in an incompressible flow, mass flow rate must remain constant.
-
Flow Visualization: Techniques to visualize fluid flow and understand complex flow patterns.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the potential function phi = 3x + 2y to derive velocity components and assess if flow is irrotational.
-
Examining the conditions under which the continuity equation is satisfied for a given flow field.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid flow, without any strife, Kinematics rules the motion of life!
📖 Fascinating Stories
-
Imagine a stream flowing smoothly over rocks, spiraling and turning without a care, embodying the essence of kinematic beauty in nature.
🧠 Other Memory Gems
-
Kinematics = movement without forces (Think Kites - they move but don't push themselves).
🎯 Super Acronyms
D.O.F = Degrees Of Freedom, the key concept in understanding fluid motion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fluid Kinematics
Definition:
The study of fluid motion without regard to the forces involved in the motion.
-
Term: Irrotational Flow
Definition:
A flow where the fluid has no rotation about any axis.
-
Term: Streamline
Definition:
A line that is tangent to the velocity vector of the flow at every point, representing the path that a fluid element follows.
-
Term: Vorticity
Definition:
A measure of the local spin of the fluid at any point, represented mathematically as the curl of the velocity field.
-
Term: Continuity Equation
Definition:
An equation that expresses the principle of conservation of mass in fluid dynamics.