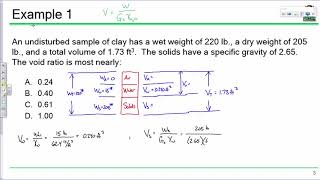
Example 2
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Soil Properties
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're discussing the critical properties of soil, particularly how we measure its state right after it arrives in the lab. Why do you think these measurements are so vital?

Because soil properties can change during transport and storage?

Exactly! We need to determine water content and unit weight to ensure our tests are accurate. It helps us understand how the soil will behave in various conditions. Can anyone tell me what dry unit weight is?

It's the weight of the soil without any water, right?

Yes, that's correct! We often calculate it using the bulk unit weight and water content. This leads us to our first formula. Remember, the acronym 'DUM' can help you recall Dry Unit Weight, Unit Weight, and Moisture Content. Let’s see how we can apply this.
Example 1: Dry Unit Weight Calculation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

In Example 1, we have a soil with a void ratio of 0.72 and a moisture content of 12%. Who can recall how we might calculate the dry unit weight with this information?

Do we use the formula involving bulk unit weight?

Correct! We can determine dry unit weight from bulk unit weight and water content. Let's do the calculations together. What results do we get for the dry unit weight?

It’s 15.51 kN/m3 based on the conversion calculations!

Good job! We’ll carry on calculating the moist unit weight and the amount of water needed for saturation next. Remember the links between these properties.
Example 2: Void Ratio and Specific Gravity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Moving on to our second example, we have a dry density of 1600 kg/m3 and a porosity of 0.387. What do you think the first step should be?

We need to find the void ratio, right?

Absolutely! Using the porosity, can anyone derive the void ratio using the formula we’ve learned?

It's like… e = n / (1-n)? So, that gives us 0.631!

Excellent! And how about the specific gravity of soil solids? What’s our approach here?

We can use the relationship between dry density, specific gravity, and the void ratio!

Exactly! Remember to note down these interrelations as they are crucial for understanding soil behavior. Great work, everyone!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The focus of this section is on understanding various properties of soil, such as dry unit weight, moisture content, and void ratio. It includes practical examples demonstrating how to compute these attributes using given values of soil properties.
Detailed
Example 2
This section emphasizes the importance of quantifying soil properties upon laboratory receipt, specifically focusing on water content and unit weight, which can vary during transportation.
Key interrelations and formulae are introduced, such as calculating dry unit weight from bulk unit weight and water content. The section provides two practical examples.
Example 1 involves determining the dry unit weight and other related measurements using provided values of void ratio, moisture content, and specific gravity.
Example 2 requires calculating void ratio and specific gravity from a known dry density and porosity of soil. The values of different soil properties are crucial in understanding soil behavior and characteristics, which can have significant implications in civil engineering applications.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Dry Density and Porosity
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Example 2: The dry density of a sand with porosity of 0.387 is 1600 kg/m3. Find the void ratio of the soil and the specific gravity of the soil solids. [Take n = 0.387 = 1600 kg/m3]
Detailed Explanation
This example introduces two important concepts in soil mechanics: dry density and porosity. Dry density is the mass of the dry soil per unit volume, typically expressed in kg/m³. In this case, we have a dry density of 1600 kg/m³. Porosity (n) is the ratio of the volume of voids to the total volume of the soil and is given as 0.387.
To find the void ratio (e), we will use the formula:
- e = n / (1 - n)
Substituting the given porosity (n = 0.387), we can calculate the void ratio.
After calculating void ratio, the next task is to find the specific gravity (G) of the soil solids. Specific gravity is a dimensionless quantity and is calculated using:
- G = (dry density of soil solids) / (density of water)
Assuming the density of water is approximately 1000 kg/m³, we can determine the specific gravity once we calculate the dry density of soil solids.
Examples & Analogies
Think of a sponge. When dry, it has a certain 'dry density' based on how much material there is inside (the solid parts of the sponge). Now, when we consider porosity, it tells us how much empty space or 'voids' are present in the sponge where water could be held. The void ratio will tell us how much of the volume of the sponge is filled with these voids compared to the solid parts, and specific gravity will help us understand how heavy the sponge is when you compare it to an equal volume of water.
Calculation of Void Ratio
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
(a) e = = = 0.631
Detailed Explanation
To calculate the void ratio (e), we use the formula:
e = n / (1 - n). Substituting the value of n:
- Start with n = 0.387.
- Calculate (1 - n):
(1 - 0.387) = 0.613. - Finally, divide n by (1 - n):
e = 0.387 / 0.613.
This results in a void ratio of approximately 0.631. The void ratio indicates how much space is available for water in the soil compared to the soil's solid components. Higher void ratios mean more space for water, which is crucial for understanding soil behavior in construction and agriculture.
Examples & Analogies
Imagine you have a jar filled with marbles (the solid parts of the soil) and there are spaces in between them (the voids). The void ratio helps us understand how many empty spaces there are compared to the number of marbles. If there are more spaces for air or water in the jar, it means the jar is less packed with marbles. This is similar to how soil can hold more water when it has a high void ratio.
Determining Specific Gravity of Soil Solids
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
(b) = G =
Detailed Explanation
After finding the void ratio, the next step is to calculate the specific gravity (G) of the soil solids. Specific gravity is calculated using the dry density of soil solids. The formula used is:
G = (Dry Density of Soil Solids) / (Density of Water).
Given the information, we assume density of water is approximately 1000 kg/m³, so:
Once we have the dry density of soil solids, simply plug in the values to find G. Specific gravity helps understand how heavy the soil solids are compared to water and is fundamental in soil mechanics, especially for comparing different soils.
Examples & Analogies
You can think of specific gravity like comparing the weight of different balls. If you have a basketball filled with air (less dense) compared to a basketball filled with sand (denser), specific gravity tells us how heavy each ball would be if both were the same size. This concept is similar to soil where different types of soil solids have varying weights contributing to their overall density and behavior.
Key Concepts
-
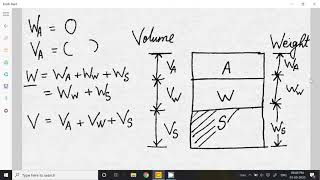
Void Ratio: A crucial property in soil mechanics representing the space available for water and air within the soil.
-
Moisture Content: Integral to comprehending how the water present affects soil stability and behavior.
-
Dry Unit Weight: Essential for understanding the load-bearing capacity of soil.
-
Specific Gravity: Important for characterizing the density of soil solids in comparison to water.
Examples & Applications
Example 1 demonstrated calculating dry unit weight and moisture content from soil properties.
Example 2 illustrated obtaining void ratio and specific gravity from known dry density and porosity.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find the weight dry in soil, remember the water's a worrisome foil.
Stories
Imagine a sandy beach, where dry grains sit and water hides nearby; observing how they balance teaches us of their ratio's tie.
Memory Tools
Every Student Can Find Density: e, S, C, F - stands for Void Ratio, Specific Gravity, and Density relationships.
Acronyms
VMD
Void
Moisture content
Dry Unit weight - all key to understanding soil properties.
Flash Cards
Glossary
- Void Ratio
The ratio of the volume of voids to the volume of solids in a soil sample.
- Moisture Content
The amount of water contained in a soil sample, expressed as a percentage of the dry weight of the soil.
- Dry Unit Weight
The weight of soil solids per unit volume of soil without any water.
- Specific Gravity
The ratio of the density of soil solids to the density of water at a standard temperature.
Reference links
Supplementary resources to enhance your learning experience.
