Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Reynolds Transport Theorem
Unlock Audio Lesson
Good morning, students! Today we'll learn about the Reynolds Transport Theorem, or RTT for short. This theorem allows us to relate the behavior of a system to a control volume, which is essential for deriving the conservation equations.
What exactly does this theorem tell us?
Great question! The RTT tells us how the properties of a fluid, like mass and momentum, behave over time in a control volume. Think of it this way: if you imagine a box in the fluid, RTT helps us analyze what's happening inside that box.
Are there different forms of this theorem?
Yes, indeed! There’s a general form and specific forms for mass and momentum. Let's focus on how it applies to mass first.
Conservation of Mass
Unlock Audio Lesson
Having discussed RTT, we move to conservation of mass. When we apply RTT for mass, we say the total mass in a control volume remains constant over time. The equation we derive is known as the continuity equation.
What does the continuity equation look like?
"It’s represented as:
Conservation of Linear Momentum
Unlock Audio Lesson
Now that we understand mass conservation, let’s talk about linear momentum. Momentum is conserved in isolated systems, similar to mass. When fluid flows and interacts, like a water jet striking a wall, momentum changes.
What happens to momentum when the water hits a wall?
Excellent question! The momentum before hitting the wall subtracts from the momentum after, which is zero. This change in momentum directly relates to the force exerted on the wall.
How do we calculate those forces?
Using the equation derived from RTT. We analyze the forces on the control volume and apply Newton’s Second Law. Remember: if the mass increases or decreases, forces change accordingly.
Applications of Conservation Principles
Unlock Audio Lesson
Let’s wrap things up by looking at some applications. The conservation of momentum appears in various hydraulic structures, like **pipes** and **elbows**.
Can you give an example?
Sure! Consider a water flow reducing elbow. When water flows through, we can use momentum equations to determine forces acting on the elbow—helpful for structural design.
That sounds important for engineers!
Absolutely! Understanding these concepts is essential for ensuring safety and efficiency in engineering design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains the conservation of momentum in fluid mechanics, detailing how it relates to Reynolds transport theorem. It discusses the formulation of conservation equations for mass and momentum, their applications in hydraulic engineering, and the principle's importance in understanding fluid flow.
Detailed
In-Depth Summary
In this section, we delve into the conservation of momentum, a crucial principle in fluid mechanics focusing on the behavior of fluids in motion. We start by introducing the Reynolds Transport Theorem (RTT), which serves as the foundation for deriving various conservation equations. Specifically, we apply the concept to mass conservation, illustrating how the total mass in a system remains constant over time. This leads us to the continuity equation:
$$
\frac{\partial}{\partial t} \int_{\text{cv}} \rho V \cdot \hat{n} dA = -\int_{\text{cs}} \rho dV
$$
which depicts the relationship between mass inflow and outflow in control volumes. Next, we transition to linear momentum, demonstrating that momentum is conserved in fluid systems and applying it to various scenarios, such as a water jet striking a wall.
We discuss how to formulate momentum equations, considering factors such as forces acting on fluids, pressure, and shear forces. Throughout the section, practical examples highlight how these concepts manifest in real-world applications, providing students with a comprehensive understanding of momentum flow in hydraulic engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Conservation of Momentum
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, starting with the last slide, where we left in the last lecture and the we derived the general form of Reynolds transport theorem here. So, this is the general form and now in the upcoming lecture and slides, what we are going to do is we will apply this Reynolds transport theorem for derivation of different conservation equations.
Detailed Explanation
In this introductory statement, the speaker revisits the concept learned in the last lecture about Reynolds Transport Theorem, which provides a framework for deriving various conservation equations in fluid dynamics. The focus will shift towards applying this theorem specifically for motion conservation, emphasizing the practical use of these concepts in hydraulic engineering.
Examples & Analogies
Think of the Reynolds Transport Theorem like a set of guidelines that help you track fluid movement as it shifts from one place to another. Just as you may track the flow of people in a busy store to understand how many enter and exit, this theorem helps us analyze and conserve quantities like momentum in fluid dynamics.
Moving to Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, now we are moving from a system to a control volume. So, we will see how when we apply B system to mass, what is going to happen. We will see about linear momentum.
Detailed Explanation
This chunk discusses a shift from analyzing entire systems to focusing on a control volume, which is a specific region in space through which fluid flows. In this context, the conservation of mass and linear momentum will be highlighted. The control volume allows for easier application of conservation laws by focusing only on the mass within that defined area, rather than the entire system.
Examples & Analogies
Imagine you are observing the flow of a river through a section you’ve marked out with ropes on either side. By focusing only on that section, you can measure how much water flows in and out, making it easier to understand the dynamics of flow rather than trying to consider the entire river at once.
Conservation of Mass
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, now conservation of mass, how can we apply what we have learned in Reynolds transport theorem to the conservation of mass. So, B is total amount of mass in the system, when we do the conservation of mass B which we saw in Reynolds transport theorem is the total amount of mass in the system.
Detailed Explanation
This section explains the concept of mass conservation in relation to the Reynolds Transport Theorem. The total mass in a system is denoted as 'B' and is crucial for analyzing fluids. The conservation of mass assures that the amount of mass entering a control volume equals the amount exiting it over time.
Examples & Analogies
Think about a bathtub. If you have the faucet running, the water level will rise until it reaches the overflow drain, at which point the amount of water entering equals the amount leaving. This is similar to how we analyze mass conservation in fluid flows.
Continuity Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, what is this, we know that in conservation of mass the total mass of the system with respect to the time DM, DM /Dt = 0. So, we can simply write in the control volume sys... This equation here, tells us that mass leaving minus mass entering is minus rate of increase of mass in the control volume.
Detailed Explanation
Here, the continuity equation is introduced, stating that the change in mass within a control volume over a period of time is zero. This equation shows that the mass flowing into the control volume minus the mass flowing out equals any accumulation of mass inside that volume, which is a foundational concept in fluid mechanics.
Examples & Analogies
Imagine a busy subway station. The number of people entering and exiting the station can be tracked. If the number of people entering matches those exiting, then the overall number of people in the station remains constant, just as the continuity equation indicates for mass in fluid flow.
Application of Momentum Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, now we are going to see, so, unit vector n cap here is normal to the surface... So, if the mass in the control volume is constant...
Detailed Explanation
In discussing momentum conservation, the text illustrates that the unit vector normal to the surface helps in calculating the momentum at the control surfaces. If the mass remains constant within the control volume, it implies that the outgoing momentum must balance the incoming momentum, which is fundamental to understanding how forces act on moving fluids.
Examples & Analogies
Picture a soccer game. When the ball is kicked, the momentum changes as the ball enters the goal area versus when it rebounds. Here, just as the soccer ball exchanges momentum with the goal posts (or players), fluid momentum is conserved as it moves through different cross-sections of a control volume.
Linear Momentum Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
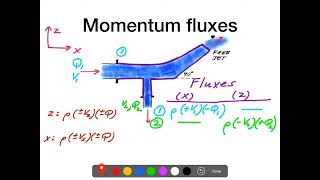
So, now the linear momentum equation. An example here is, if you see this figure here... So, here we can actually apply the momentum conservation linear momentum.
Detailed Explanation
The linear momentum equation is introduced through an example where water is shot against a wall. Here, the momentum before hitting the wall is compared to the momentum after, demonstrating a change in momentum. This scenario serves to highlight the practical application of momentum conservation principles in real-life fluid mechanics.
Examples & Analogies
Think of it like throwing a basketball against a wall. The ball has momentum as it approaches and comes to a stop upon hitting the wall. The change in momentum relates directly to the force applied to the wall, similar to the linear momentum discussion in fluid scenarios.
Practical Application and Example Problems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, now let’s discuss some examples of mass conservation, the flow out of a reservoir... So, Q out will be simply - area of reservoir into d h / dt or we can simply write the rate of fall of height with respect to time is this - Q / area of the reservoir.
Detailed Explanation
This chunk introduces practical applications of the conservation of mass and linear momentum through example problems. By calculating the flow of fluid from a reservoir, the relationship between flow rate, area, and height is highlighted, illustrating how these principles are intertwined and useful in engineering calculations.
Examples & Analogies
Visualize a reservoir filled with water. If you have a spout at the bottom, and you know how fast water flows out, you can easily calculate how quickly the water level drops. This calculation is similar to how engineers use mass conservation principles to manage water resources.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Transport Theorem: A theorem that connects system behavior to control volume analysis.
-
Conservation of Mass: The principle that total mass remains constant within a closed system.
-
Conservation of Linear Momentum: The principle that the total momentum of a closed system remains unchanged.
-
Continuity Equation: An equation that expresses the relationship between inflow and outflow rates of mass in a control volume.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A water jet striking a wall demonstrates how momentum is conserved as the force from the jet is exerted on the wall.
-
Flow through a reducing elbow in a piping system illustrates how pressure and velocity interact and how to apply the momentum equation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To keep the flow and mass intact, Reynolds helps us stay on track!
📖 Fascinating Stories
-
Imagine water flowing in a pipe; the flow is constant, like a steady pipe dream, helped by Reynolds guiding its stream.
🧠 Other Memory Gems
-
Use RCM to remember: R for Reynolds, C for Continuity, M for Mass Conservation.
🎯 Super Acronyms
MOM
- Mass
- Outflow
- Momentum - to memorize conservation concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reynolds Transport Theorem
Definition:
A foundational principle that relates the change of a property in a control volume to the flow across its boundaries.
-
Term: Control Volume
Definition:
A defined region in space through which fluid flows, used for analyzing mass and momentum conservation.
-
Term: Continuity Equation
Definition:
An equation that describes the conservation of mass in a fluid flow system.
-
Term: Momentum
Definition:
The product of the mass and velocity of an object, representing its motion.
-
Term: Fluid Dynamics
Definition:
The study of fluids in motion and the forces acting upon them.