Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Barometers
Unlock Audio Lesson
Today, we will start our exploration of barometers, which are fascinating devices used to measure atmospheric pressure. Can anyone tell me what atmospheric pressure is?
It's the weight of air pressing down on us.
Great! Atmospheric pressure is indeed the force exerted by the weight of air. A barometer measures this pressure by indicating the height of mercury—how high can mercury rise by atmospheric pressure?
It can rise to 750 mm in some cases, right?
Absolutely! And this height corresponds to the local atmospheric pressure at that point. Remember, R equals 750 mm of Hg, which is crucial for our calculations.
Could you explain how this measurement translates into a pressure value?
Certainly! We can use the equation P = S * R to calculate the pressure in Pascals. Here, S is the density of mercury, and R is the height in millimeters.
Oh! So, if the gauge pressure is 0, the absolute pressure would just be P1?
Exactly! And that takes us to the next topic—how pressure changes in compressible fluids. But first, can anyone summarize what we learned about barometers?
Barometers measure atmospheric pressure using the height of mercury, which relates to the pressure through the formula P = S * R.
Pressure Variations in Gases
Unlock Audio Lesson
Now let's transition to pressure variations! We have two key processes for gases: isothermal processes and ones with a constant temperature gradient. Is anyone familiar with these terms?
Isothermal means the temperature stays the same throughout?
Precisely! In an isothermal process, we can use the ideal gas law, PV = nRT. How does this help us understand pressure as we move from one point to another?
We can integrate, right? It leads to the natural logarithm of the pressure ratio.
Exactly! The equation we derive is: P2 = P1 * e^[-(Mg/RT)(Z2-Z1)]. This shows how pressure drops with altitude in our atmosphere. Can anyone think of why this is essential in meteorology?
It helps predict weather patterns based on pressure changes!
Right! Understanding these changes correlates with weather and climate dynamics. Summarize this process so far.
In isothermal expansion, the pressure decreases when altitude increases, correlating to the temperature and gas behavior.
Manometers and Other Measurement Devices
Unlock Audio Lesson
Now let's discuss other important devices! Besides barometers, we also have manometers. Can anyone explain the differences?
Manometers measure pressure differences between two points, while barometers measure absolute pressure.
Exactly! And they use the same principles of hydrostatic pressure and fluid columns. What are some applications you think of for manometers?
They can be used in labs to measure pressure in gas and liquid systems!
Correct! They play vital roles in engineering. Suppose I have water at 500 kPa pressure. How would you calculate the height in a water manometer?
We would use the formula h = P / (density * g). So that's 500,000 / 9800!
Yes! And what does this height indicate?
It indicates how high the water will rise in the manometer based on that gauge pressure!
Example Problems in Pressure Measurement
Unlock Audio Lesson
Let’s tackle some example problems together! What if we have a pressure of 500 kPa measured in a water distribution system? What's our first step?
We would first convert the pressure into height in the manometer.
Exactly! And remember, the density of water is about 9800 N/m³. What height do you calculate?
The height comes out to be around 51 meters!
Because mercury is denser, resulting in a more manageable column height!
Excellent observation! Can we summarize what we've learned about pressure calculating techniques and their importance?
We've learned how to calculate pressure using several different fluids and the importance of those measurements in real-world applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how barometers work to measure atmospheric pressure, delve into the relationship between pressure and fluid dynamics, and discuss different types of pressure measurement devices. Practical examples illustrate how to calculate pressure using barometric readings.
Detailed
Introduction to Barometers
In this section, we delve into the fundamentals of barometers and their role in measuring atmospheric pressure. A barometer traditionally measures the height of mercury in a column due to atmospheric pressure acting upon it. We begin by discussing how to calculate atmospheric pressure when R is at 750 millimeters of mercury (Hg) and highlight the relationship between pressure readings and piezometric head.
We introduce two important concepts concerning pressure variations in compressible fluids: the isothermal process and the constant temperature gradient for gases. These principles lead to a deeper understanding of how pressure is expressed in gases and liquids and the impact of temperature on these measurements.
Furthermore, we cover the comparison of barometers with other pressure measurement devices such as manometers and pressure transducers, highlighting their unique features and how they are applied in real-world scenarios such as water distribution systems. The examples provided help to elucidate the various calculations involved in deriving pressures from the measurements taken, solidifying the students' understanding through practical application.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Barometers and Atmospheric Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, this is the barometer. This is the principle of working of barometers. Now, a simple question is, what is the local atmospheric pressure when R is 750 millimeters of Hg. This is R we are just going to see we have given the =13.6 then we have assumed incompressible fluid constant, we are going to see how it works.
Detailed Explanation
This chunk introduces what a barometer is and its function in measuring local atmospheric pressure. It mentions the specific measurement of mercury height (R) and introduces the fluid density constant (13.6). In practical terms, R (the height of mercury) is indicative of atmospheric pressure, and it’s crucial to understand these constants to evaluate pressure accurately.
Examples & Analogies
Imagine a simple water column in a tube. If you fill it up, the height of the water indicates how much air pressure is pushing down on the water from above. Similarly, in a barometer, the height of the mercury column tells us how much atmospheric pressure is currently acting on it.
Calculating Pressure with Piezometric Head
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we have seen this equation piezometric head is constant. So, we can write let me erase this one. P1 is . We are putting this piezometric head equation between point 1 and point 2 and we want to calculate the pressure at p1. p 2 atmospheric pressure so, atmospheric pressure we assume gauge pressure that can be assumed 0.
Detailed Explanation
This chunk discusses the principle of piezometric head, stating that it remains constant in a given system. This is important when calculating pressure at various points. It utilizes the assumption that gauge pressure is 0, indicating pressure measurement relative to atmospheric pressure, allowing us to understand how pressure at point 1 relates to atmospheric pressure.
Examples & Analogies
Think of it like a playground slide. The height of the top of the slide (piezometric head) remains constant, allowing children at different heights (point 1 and point 2) to experience different speeds while we assume no significant friction (gauge pressure as 0) affects their descent.
Understanding Pressure Variation in Compressible Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we must also be a little aware about the pressure variations in a compressible fluid. There are 2 processes, one is perfect gas at constant temperature isothermal that we have been seeing till now.
Detailed Explanation
This chunk introduces the concept of pressure variations in compressible fluids, particularly focusing on perfect gases under different conditions. It highlights isothermal processes (constant temperature) as significant when considering how gas behaves under changing pressures.
Examples & Analogies
Imagine a balloon. If you squeeze the balloon (increase pressure), but keep it in a warm room (constant temperature), the balloon's material responds by stretching (changing volume) rather than only increasing in pressure. This showcases the relationship between pressure and volume in gases.
Integrating Pressure and Temperature Relationships
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, in case of constant temperature isothermal the perfect gas, the pressure variation will be like this. So, very simple derivation but a little more intriguing than the one that we did before for; you know, pressure variation within the liquid where we got simply piezometric head.
Detailed Explanation
In this part, a mathematical relationship is presented that shows how pressure varies with height under isothermal conditions. The relationship utilizes natural logarithms, indicating that as you move vertically, the pressure behaves logarithmically in terms of height differences.
Examples & Analogies
Consider riding a bike uphill. The higher you ride, the more effort you need (akin to needing more pressure). However, the change in effort is not linear; it increases at a different rate based on how steep the hill is, similar to how we calculate pressure changes at varying heights.
Introduction to Pressure Measurement Devices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
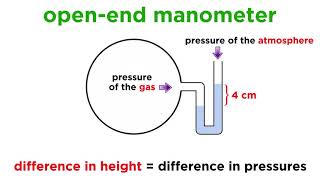
Pressure measurement devices, we have discussed one already barometers, there are manometers a standard manometer or a differential manometer and the pressure transducers. This is out of the scope, but you must have already done it in your fluid mechanics class.
Detailed Explanation
This chunk lists various instruments used for measuring pressure, starting with barometers and then mentioning manometers and pressure transducers. This introduction sets the stage for understanding the differences and applications of each type of device.
Examples & Analogies
Think of measuring your weight at home (barometers) versus tracing your weight changes over time with a specialized scale (manometer). While both measure weight (pressure), they do so in slightly different ways for specific needs.
Applications of Standard and Differential Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For standard manometers. What is the pressure? So how it works is very simple example. So, what is if we are asked, what is the pressure at A given the height...
Detailed Explanation
This chunk illustrates practical applications of standard and differential manometers for measuring pressures. It discusses how parameters like height of liquid in a tube relate to actual pressure calculations, exemplifying practical use in fluid systems.
Examples & Analogies
Imagine checking water levels in a bathtub. The height of water above a certain point correlates directly to pressure pushing down. A manometer operates similarly, using the height of a liquid column to determine pressure at a point in a system.
Understanding Gauge Pressures in Measurement Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, how high would the water rise in a manometer connected to a pipe containing water at 500 kPa...
Detailed Explanation
This includes a scenario where the pressure in a water distribution system is discussed in terms of gauge pressure, emphasizing how much higher the water would rise in a connected manometer based on known pressures.
Examples & Analogies
Think about filling a soda bottle. When the bottle is sealed, the pressure inside builds up. When you open it, the liquid height adjusts quickly based on the pressure, similar to how a manometer reflects pressure changes when attached to a different system.
Differential Manometers and Gauge Pressure Measurement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Another example for a differential you know, manometer...
Detailed Explanation
This chunk focuses on how to find gauge pressure using differential manometers involving different fluid densities. It shows the relationship between different points in a system, adding depth to previous discussions.
Examples & Analogies
Consider a seesaw where one side has two children and the other has a single adult. The weights balance differently based on their positions. A differential manometer observes similar principles, comparing pressures across different points in order to measure forces accurately.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Atmospheric Pressure: The weight of air above us, measured by devices like barometers.
-
Piezometric Head: Represents the potential energy of a fluid due to its height.
-
Isothermal Process: A thermodynamic process where temperature remains constant during expansion or compression.
-
Gauge Pressure: The pressure measured above atmospheric pressure.
-
Hydrostatic Pressure: The pressure exerted by a fluid at a given depth due to the weight of the fluid above it.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If atmospheric pressure is typically 101,325 Pa, in terms of mercury height, this corresponds to approximately 760 mm of Hg.
-
In a water distribution system, a gauge reading of 500 kPa would cause a water manometer to rise about 51 m if using water.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the air is high and the mercury's still, the barometer reads, weather it’ll fulfill.
📖 Fascinating Stories
-
Imagine a tall mercury column standing proud; it speaks of the weather, through the air it calls loud.
🧠 Other Memory Gems
-
Remember 'BAP' for Barometer’s function: to Measure Atmospheric Pressure!
🎯 Super Acronyms
B.P.M. - Barometer, Pressure Measurement!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Barometer
Definition:
An instrument that measures atmospheric pressure, typically using a column of mercury.
-
Term: Piezometric head
Definition:
The potential energy of a fluid in relation to its elevation compared to a reference point.
-
Term: Isothermal Process
Definition:
A thermodynamic process in which the temperature remains constant.
-
Term: Gauge Pressure
Definition:
The pressure relative to atmospheric pressure, typically measured in Pascals or bars.
-
Term: Manometer
Definition:
A device used to measure the pressure of a fluid by comparing it to atmospheric pressure.
-
Term: Hydrostatic pressure
Definition:
The pressure exerted by a fluid at equilibrium due to the force of gravity.