Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Exponents
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome to today's lesson on exponents! Can anyone tell me what an exponent represents?
An exponent shows how many times to multiply a number by itself.
Exactly! For example, in 24, the '2' is the base and '4' is the exponent. So, 24 = 2 × 2 × 2 × 2. Why do we use exponents?
To make large numbers easier to read and work with!
Correct! Now, let’s move on to the laws of exponents that help us manipulate these expressions.
Product of Powers Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The first law is the Product of Powers Law. If I have am × an, how do we simplify it?
Add the exponents, right?
That's right! So 32 × 34 = 32+4. What does that equal?
36, which equals 729!
Perfect! Remember, you can think of it as 'adding powers' just like addition. Let's summarize this: If you multiply, you add the exponents!
Quotient of Powers Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's discuss the Quotient of Powers Law. If I divide am by an, what do we do?
We subtract the exponents!
Exactly! So if I say 56/52, what does that equal?
54!
Right! And remember, this only works when the base is the same and is not zero.
Power of a Power Law and Examples
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next up is the Power of a Power Law. If I have (am)n, what do we do?
We multiply the exponents!
Correct! For example, (23)2 = 23×2. What does this simplify to?
26, which is 64!
Great job! Remember the acronym 'M-P' for Multiply Exponents when you see a power raised to another power!
Review and Applications
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To wrap up, we have learned about the Product, Quotient, and Power of a Power Laws. Can each of you summarize one of the laws?
The Product of Powers means we add exponents!
The Quotient of Powers means subtract exponents!
Power of a Power means multiply the exponents!
Well done, everyone! Remember these laws as they'll be vital for your future math studies, especially when we dive into more complex equations!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the fundamental rules of exponents in algebra, including the product, quotient, power of a power, and other laws that facilitate the simplification of exponential expressions and equations. Mastering these laws is critical for students learning scientific notation and polynomial expressions.
Detailed
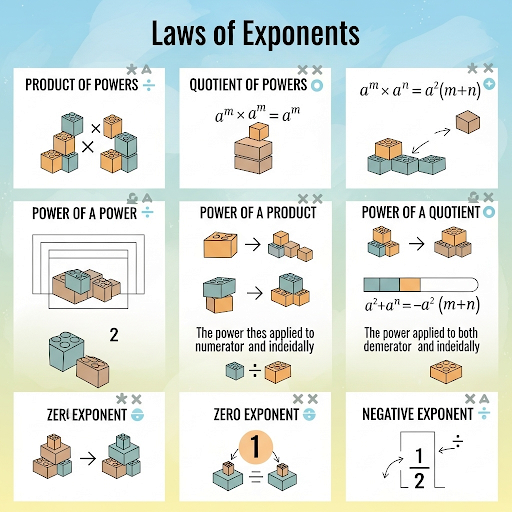
Laws of Exponents
Exponents, referred to as powers or indices, allow for a simplified representation of large numbers and are a foundational concept in algebra. This section elaborates on the various laws that dictate the operations involving exponents, crucial for mastering algebraic manipulations.
- Product of Powers Law: When multiplying two powers with the same base, the exponents are added: 𝑎𝑚 × 𝑎𝑛 = 𝑎𝑚+n. For example, 32 × 34 = 36 = 729.
- Quotient of Powers Law: When dividing powers with the same base, subtract the exponent of the denominator from the exponent of the numerator: 𝑎𝑚/𝑎𝑛 = 𝑎𝑚−n. E.g., 56/52 = 54 = 625.
- Power of a Power Law: Raising a power to another power involves multiplying the exponents: (𝑎𝑚)𝑛 = 𝑎𝑚×n. For instance, (23)2 = 26 = 64.
- Power of a Product Law: When raising a product to a power, apply the exponent to each factor: (𝑎𝑏)𝑚 = 𝑎𝑚 × 𝑏𝑚. Example: (3×4)2 = 144.
- Power of a Quotient Law: When raising a quotient to a power, apply the exponent to both the numerator and denominator: (𝑎/𝑏)𝑚 = 𝑎𝑚/𝑏𝑚.
- Zero Exponent Law: Any non-zero base raised to the power of zero equals 1: 𝑎0 = 1. Example: 70 = 1.
- Negative Exponent Law: A negative exponent signifies the reciprocal of the base raised to the positive exponent: 1/𝑎−𝑛 = 𝑎𝑛.
Additionally, converting exponential expressions into scientific notation provides a way to express very large or small numbers compactly. Understanding these laws enables students to simplify complex expressions and solve equations effectively.
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Product of Powers Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When multiplying two powers with the same base, add their exponents.
Example:
32 × 34 = 32+4 = 36 = 729
Detailed Explanation
The Product of Powers Law states that when you have two exponents with the same base being multiplied, you simply add their exponents. For instance, if you have 2 raised to the power of 3 multiplied by 2 raised to the power of 4 (which is written as 2³ × 2⁴), you add the exponents (3 + 4) to get 2 raised to the power of 7 (2⁷). This results in 128.
Examples & Analogies
Think of this like stacking boxes. If you have a stack of 3 boxes and you add another stack of 4 boxes, you end up with a total of 7 boxes. The exponent helps us quickly count the total number of boxes (or multiplications) without explicitly writing them all out.
Quotient of Powers Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When dividing powers with the same base, subtract the exponent of the denominator from that of the numerator.
Example:
56 ÷ 52 = 56−2 = 54 = 625
Detailed Explanation
The Quotient of Powers Law tells us how to simplify expressions where the same base is divided. For instance, if you have 5 raised to the power of 6 divided by 5 raised to the power of 2 (5⁶ ÷ 5²), you subtract the exponents (6 − 2), yielding 5 raised to the power of 4 (5⁴), which equals 625.
Examples & Analogies
Imagine you have 6 apples and you give away 2 apples. The total apples you have left can be thought of as subtracting the amount given away from your original amount, similar to how we subtract the exponents.
Power of a Power Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When raising a power to another power, multiply the exponents.
Example:
(23)2 = 23×2 = 26 = 64
Detailed Explanation
According to the Power of a Power Law, when you take a power and raise it again to another power, you multiply the exponents. For example, in (2³)², you multiply the exponents 3 and 2 (3 × 2), resulting in 2 raised to the power of 6 (2⁶), which equals 64.
Examples & Analogies
Imagine you are watching a movie trilogy. If each movie is 3 hours long and you plan to watch it twice, you would multiply the hours per movie by the number of times you plan to watch them. This is similar to how we multiply the exponents when applying the power of a power rule.
Power of a Product Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When raising a product to a power, apply the exponent to each factor.
Example:
(3×4)2 = 32 × 42 = 9×16 = 144
Detailed Explanation
The Power of a Product Law indicates that when you have a product raised to a power, you apply that power to each factor within the parentheses. For instance, if you have (3×4)², you square both numbers: 3² and 4², giving you 9 and 16, respectively. Their product is therefore 144.
Examples & Analogies
Think of it like baking cookies. If you have a recipe that requires 3 cups of sugar and you double the recipe, you would calculate 2 times each ingredient separately: 2×3 for sugar and then multiply the other ingredients—similar to applying the exponent to each part of the product.
Power of a Quotient Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When raising a quotient to a power, apply the exponent to both the numerator and denominator.
Example:
(2/5)3 = 2³/5³ = 8/125
Detailed Explanation
The Power of a Quotient Law states that when you raise a fraction to a power, you apply the exponent to both the numerator and the denominator. For example, if you have (2/5)³, you cube both 2 and 5 separately, resulting in 2³ (which is 8) and 5³ (which is 125). Therefore, (2/5)³ equals 8/125.
Examples & Analogies
Think of this as packing boxes for shipping. If each box can hold 2 items out of a total of 5 items (the full package), when you pack more boxes, you need to assess both the contents (the items, the numeral) and the overall box capacity (the denominator).
Zero Exponent Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Any non-zero base raised to the power of zero equals 1.
Example:
70 = 1, (−3)0 = 1
Detailed Explanation
The Zero Exponent Law states that any number, except zero, raised to the power of zero equals one. For example, 7⁰ equals 1, and even (-3)⁰ equals 1. This law helps simplify expressions and clarifies that a base with no multiplication (zero exponent) results in one.
Examples & Analogies
Picture a light bulb that is off. Even though it's off (like being raised to zero), it still has the potential to turn on (just like the number itself still has a value of 1).
Negative Exponent Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A negative exponent indicates the reciprocal of the base raised to the positive exponent.
Example:
2−3 = 1/23 = 1/8
Detailed Explanation
The Negative Exponent Law tells us that a negative exponent means you take the reciprocal of the base and change the exponent to positive. For instance, 2 raised to -3 (2⁻³) is the same as 1 divided by 2 raised to the positive 3 (1/2³), which equals 1/8.
Examples & Analogies
Think of it as taking a step back. If you owe someone money (a negative amount), their value exists as the opposite of what you owe; flipping from negative to positive gives you clarity about your balance.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Exponents: Numbers indicating the number of times a base is multiplied by itself.
-
Product of Powers Law: States that am × an = am+n.
-
Quotient of Powers Law: Involves subtracting exponents when dividing powers with the same base: am/an = am−n.
-
Power of a Power Law: Involves multiplying exponents when raising a power to another power: (am)n = am×n.
-
Power of a Product Law: Applies the exponent to each factor in a product: (ab)m = am × bm.
-
Zero Exponent Law: Says any non-zero base raised to zero equals 1.
-
Negative Exponent Law: Indicates the reciprocal of the base raised to the positive exponent.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of Product of Powers: 32 × 34 = 36 = 729.
-
Example of Quotient of Powers: 56/52 = 54 = 625.
-
Example of Power of a Power: (23)2 = 26 = 64.
-
Example of Power of a Product: (3×4)2 = 32 × 42 = 144.
-
Example of Zero Exponent: 70 = 1.
-
Example of Negative Exponent: 2−3 = 1/(23) = 1/8.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To multiply, add the powers, that’s the way, it’s clear as day!
📖 Fascinating Stories
-
Imagine you are baking a cake. Each layer represents an exponent. When you stack layers (multiply), you need to count all the layers (add exponents) together!
🧠 Other Memory Gems
-
M-P-Q-Z-N: Multiply (add), Power (multiply), Quotient (subtract), Zero = 1, Negative = reciprocal.
🎯 Super Acronyms
Remember 'Exponent Rules' can be saved as 'E-R' to keep track of Exponent Laws!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Exponent
Definition:
A number indicating how many times to multiply the base by itself.
-
Term: Base
Definition:
The number that is raised to a power in exponentiation.
-
Term: Product of Powers Law
Definition:
When multiplying two powers with the same base, add the exponents.
-
Term: Quotient of Powers Law
Definition:
When dividing powers with the same base, subtract the exponent of the denominator from that of the numerator.
-
Term: Power of a Power Law
Definition:
When raising a power to another power, multiply the exponents.
-
Term: Power of a Product Law
Definition:
When raising a product to a power, apply the exponent to each factor.
-
Term: Zero Exponent Law
Definition:
Any non-zero base raised to the power of zero equals 1.
-
Term: Negative Exponent Law
Definition:
A negative exponent indicates the reciprocal of the base raised to the positive exponent.