Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Concept of a Limit
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
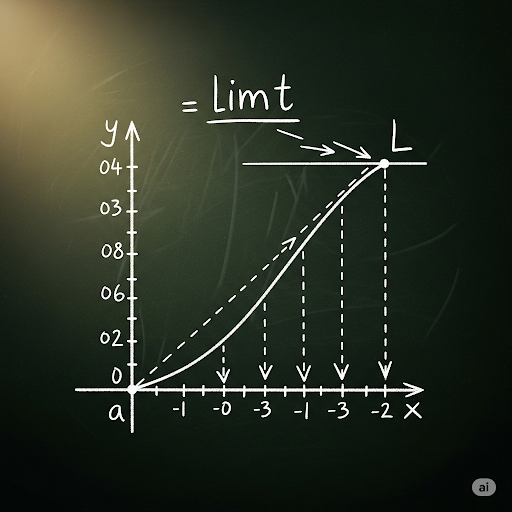
Today, we’re going to learn about limits. A limit is the value a function approaches as the input approaches a specific value. For example, if we have a function f(x) and as x gets closer to a value a, f(x) approaches a value L, we write this as lim f(x) = L as x approaches a.
So, it's about what happens to f(x) when x gets close to a?
Exactly! You can think of limits as how our input x influences the output f(x) as we creep up to a certain point.
Is that like when you try to get right to the edge of a cliff, but you never actually go over?
Great analogy! You're getting close but not actually touching it. Let's summarize: limits model behavior at specific points.
Evaluating Limits from a Table
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, we’ll figure out limits using a table. If we can't plug x = a directly, we can approximate its value. For instance, if we evaluate lim (x^2 + 3) as x approaches 2, we can create a table with values near 2.
Do we just take points smaller and larger than 2?
Exactly! You'd look at values like 1.9, 1.99, 2, 2.01, and 2.1. What do you think we’ll find?
It looks like it's getting close to 7!
Correct! So lim (x^2 + 3) as x approaches 2 equals 7. Good observation on the table results!
Evaluating Limits Graphically
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
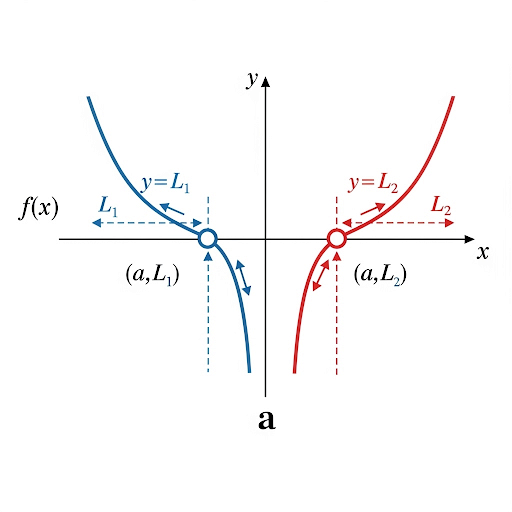
Now let's discuss how to evaluate limits graphically. By looking at a graph, we can determine the limit by observing values from both sides as x approaches a certain point.
What if the graph shows different values from each side?
Great question! If the left side and right side converge to different values, the limit does not exist or DNE.
Can you show us an example?
Sure! If we look at a graph where f(x) approaches 5 from the left and 3 from the right as x approaches a, we say the limit as x approaches a does not exist.
Got it! So we can't say the limit is 4, since it's undefined.
Algebraic Evaluation of Limits
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let’s do algebraic evaluation. For simple functions, direct substitution works great. But sometimes we have indeterminate forms like 0/0. In these cases, we simplify first!
So, if we had lim (x^2 - 1)/(x - 1) as x approaches 1, we'd need to factor it first?
Right! Factor as (x - 1)(x + 1) to cancel out the (x - 1). Then you can find the limit by substituting.
That makes sense! So we can get the limit by substituting 1 into x + 1.
Exactly! It becomes 2, showing how limits can simplify complex-looking functions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Limit
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A limit is the value that a function approaches as the input (or variable) approaches a certain value.
Detailed Explanation
In calculus, a limit refers to the behavior of a function as its input gets closer to a specific point. If we denote the function as 𝑓(𝑥) and a particular value as 𝑎, we express the limit of 𝑓(𝑥) as 𝑥 approaches 𝑎 as: lim𝑓(𝑥) = 𝐿 (𝑥→𝑎). This means that as 𝑥 gets very close to 𝑎, the values of 𝑓(𝑥) get very close to 𝐿, the limit. Understanding this concept is crucial for analyzing functions and their behaviors.
Examples & Analogies
Imagine you're trying to measure how close you can get to a brick wall without actually touching it. As you step closer and closer to the wall (approaching that limit), you're getting nearer to the wall's surface but never really crossing it. In calculus, we look at how functions behave as we get near a certain value without necessarily reaching it.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
A limit describes the behavior of a function as x approaches a specific value.
-
Direct substitution can evaluate many limits.
-
One-sided limits focus on the approach from one direction.
-
Infinite limits indicate that a function heads toward infinity.
-
Limits can be classified as existing or non-existing (DNE).
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Evaluating lim (x^2 + 3) as x approaches 2 gives us 7.
-
Using a table, we found limits close to a certain point.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When limits are clear, don’t fear, just plug in, they’re near!
📖 Fascinating Stories
-
Imagine you are inching towards a treasure marked by x. Closer and closer you get, and even though you never step on it, you sense its value from afar.
🧠 Other Memory Gems
-
Use 'DIRE' for 'Direct substitution', 'Indeterminate forms', 'Right-hand limit', 'Evaluate from tables' when thinking about limits.
🎯 Super Acronyms
Remember 'LIFE'
- Limit Indicates Function’s Ending.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Limit
Definition:
The value that a function approaches as the input approaches a given point.
-
Term: Direct Substitution
Definition:
Plugging the value directly into the function to find the limit, if defined.
-
Term: Indeterminate Form
Definition:
A form that does not provide a clear limit, such as 0/0.
-
Term: OneSided Limit
Definition:
The limit approached from one direction, either left or right.
-
Term: Infinite Limit
Definition:
A limit where the function increases or decreases indefinitely.
-
Term: DNE (Does Not Exist)
Definition:
A term used when a limit cannot be determined.