Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Mean
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we will start with the mean, which is often referred to as the average. Does anyone know how to calculate the mean?
Isn't it just adding all the numbers together and then dividing by how many there are?
Exactly! The formula is the sum of all data values divided by the number of values. It’s represented as 𝑥̅ = ∑𝑥ᵢ / 𝑛. This gives us a central point around which our data is distributed.
How does that help us understand how spread out the data is?
Great question! The mean alone doesn’t tell us about the spread. This is where we introduce variance and standard deviation.
Can you explain how variance works?
Sure! Variance measures how far each data point is from the mean and thus from every other data point. We find it by calculating the average of the squared differences from the mean.
So that’s why we square the differences, to avoid negatives!
Correct! It ensures that we are measuring the spread without any cancellation of numbers.
Variances and Standard Deviations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's talk about variance. For a population, we use the formula 𝜎² = ∑(𝑥 − 𝜇)² / 𝑁. Who can tell me what each symbol represents?
𝜎 is the standard deviation, right?
Not quite, 𝜎² is the variance. 𝜇 is the population mean, ∑(𝑥 − 𝜇)² is the sum of the squared deviations, and 𝑁 is the population size. Do you see why we divide by 𝑁?
Because we want the average of those squared differences.
Exactly! Now, for the standard deviation, we simply take the square root of the variance. This gives us a measure in the same scale as our data.
Can you give an example of how this works?
Absolutely! Let’s say we have marks: 3, 5, 7, 5, and 10. First, we find the mean, then the deviations, square them, calculate variance, and finally derive the standard deviation.
That sounds like a lot of steps!
It may seem so, but once we practice, it becomes easier. Let's summarize what we learned: variance shows how spread out our values are, while standard deviation helps to express that spread in a meaningful way.
Application to Grouped Data
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we’ve covered basic data set calculations, let’s look at grouped data. For grouped data, we use midpoints and frequencies. The mean is calculated as 𝑥̅ = ∑𝑓𝑥 / ∑𝑓. What does 𝑓 represent?
It represents the frequency of each class!
Absolutely! After finding the mean, we multiply the frequency by the squared differences from the mean to find variance. Can anyone give me an example of grouped data?
What about marks distributed in intervals like 0-10, 10-20, loading towards higher marks?
Great example! We can calculate it step by step, using midpoints of each interval. This helps us estimate variance and standard deviation for large sets of data.
What's the importance of knowing these measures?
Good question! Knowing variance and standard deviation is crucial in fields like finance for risk analysis or in quality control to ensure product standards.
So they help understand the reliability of data?
Exactly! This understanding helps us make more informed decisions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Measures of Dispersion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In everyday life, we often observe variation in data—be it in test scores, heights of students, or daily temperatures. Measures of central tendency (like mean or median) tell us where data is centered, but they don't reveal how spread out the data is. For that, we need measures of dispersion, and two key ones are Variance and Standard Deviation.
Detailed Explanation
In statistics, understanding how data varies or spreads is essential because it gives us context on the consistency of the data. While measures like mean provide a central value, they don't show how far individual data points might be from that average. Therefore, concepts like variance and standard deviation become vital. Variance measures the average of the squared deviations from the mean, while standard deviation is the square root of that variance, providing a measure that is in the same units as the data.
Examples & Analogies
Think of it like a classroom where students receive different test scores. Just knowing the average score (mean) can be misleading if some students scored very high while others scored very low. Thus, knowing how much the scores deviate from the average (using variance and standard deviation) gives teachers better insight into overall student performance.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Variance: A measure of dispersion indicating average squared deviations from the mean.
-
Standard Deviation: The square root of variance, giving insight into data spread.
-
Grouped Data: Data organized into intervals that require specific methods for calculating mean and standard deviation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For data points 3, 5, 7, 5, and 10, the mean is 6, variance is 7, and the standard deviation is approximately 2.65.
-
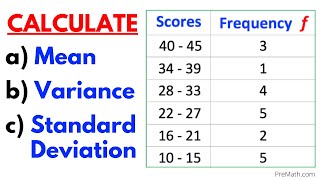
For grouped data with intervals like 0–10, 10–20, and frequencies associated with them, the standard deviation can be calculated using class midpoints.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When you find the spread of data, let the squares take a shot; square those diffs from the mean, give variance a thought.
📖 Fascinating Stories
-
Imagine a class giving their test scores. The teacher found the average, but some scores were way off the list. By calculating variance, they realized some students were lost in the mist!
🧠 Other Memory Gems
-
To remember the steps: Mean, Deviations, Square, Average. 'MDSA' helps you process—mean first, then handle!
🎯 Super Acronyms
DIVE—Deviation, Interval, Variance, Evaluation. Use it to remember the flow in calculating std. deviation!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mean
Definition:
The average of a set of numbers, calculated by dividing the sum of all values by the number of values.
-
Term: Variance
Definition:
A measure of how far each number in a set is from the mean, calculated as the average of the squared differences from the mean.
-
Term: Standard Deviation
Definition:
The square root of the variance, representing the average distance of each data point from the mean in the same units as the data.
-
Term: Population
Definition:
The complete set of items or individuals from which a sample can be drawn.
-
Term: Sample
Definition:
A subset of individuals or observations selected from a population.
Detailed Summary
In this section, we delve into the critical statistical measures of variance and standard deviation that describe the spread of data points in a dataset. While measures of central tendency like the mean or median pinpoint where the data is centered, variance and standard deviation offer insight into how data points deviate from this center. Variance quantifies the average of the squared differences from the mean, giving us a sense of data dispersion, while the standard deviation presents this dispersion in the same unit as the data, making it easier to interpret. The section also includes step-by-step examples of calculating these measures for sample and grouped data and discusses their significance in fields like finance, science, and quality control.