Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hardy-Weinberg Equilibrium
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we are going to learn about the Hardy-Weinberg Principle, which helps us understand genetic variation in populations. Can anyone tell me what they think a gene pool is?

Isn't it the collection of all genes in a population?

Exactly, Student_1! A gene pool includes all genes and their alleles in a population. Now, can anyone guess why a large gene pool is beneficial?

It probably helps with adaptation and survival!

Correct! A larger gene pool represents higher genetic diversity, giving populations a better chance to adapt. Now let’s move on to discussing the key assumptions of the Hardy-Weinberg Principle. Who can list them?

I think it needs a large population, random mating, no mutations, no migration, and no natural selection.

Great job, Student_3! These conditions must all be met for a population to be in equilibrium. Let's review why each condition is important.
Hardy-Weinberg Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now let’s dive into the mathematical side with the Hardy-Weinberg equations. For a gene with two alleles, A (dominant) and a (recessive), we express their frequencies as `p` and `q`. Who can tell me how these frequencies relate?

`p + q = 1`, right?

Well done, Student_4! And how do we predict the genotype frequencies from these allele frequencies?

Using `p²`, `2pq`, and `q²`!

Exactly! So the full equation is `p² + 2pq + q² = 1`. This allows us to determine the expected frequencies of the genotypes in our population. Why do you think these equations might be useful?

We can use them to predict how diseases spread in a population!

Absolutely, Student_2! It helps us estimate carrier frequencies for genetic conditions. This is an important application of the Hardy-Weinberg Principle.
Applications and Real-World Examples
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Lastly, let's discuss the real-world applications of the Hardy-Weinberg Principle. What do you think deviations from equilibrium indicate in a population?

It could mean that something is changing in the population, like evolution?

That's correct! Deviations from the expected allele frequencies can suggest evolutionary changes. What could cause these changes?

Things like natural selection or mutation could change allele frequencies.

Right! And remember, gene flow and genetic drift can also impact them. So understanding these concepts helps scientists determine how populations evolve over time. Great discussion today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section outlines the Hardy-Weinberg Principle, detailing the conditions required for a population to achieve equilibrium, the relevant equations to calculate allele and genotype frequencies, and applications of the principle in estimating carrier frequencies and detecting evolutionary changes.
Detailed
Hardy-Weinberg Equilibrium
The Hardy-Weinberg Principle provides a foundational framework for studying genetic variation in populations. It posits that allele and genotype frequencies remain stable over generations, provided that certain ideal conditions are met. These conditions include a large population size, random mating, no mutations, no migration, and no natural selection.
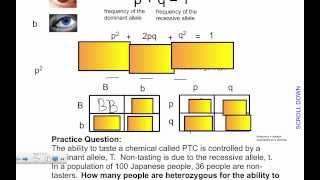
For proteins with two alleles, A (dominant) and a (recessive), we can represent allele frequencies as:
- Let p be the frequency of allele A
- Let q be the frequency of allele a
The relationship between these frequencies is characterized by the equation:
- p + q = 1
Additionally, the genotype frequencies follow:
- p²: homozygous dominant genotype (AA)
- 2pq: heterozygous genotype (Aa)
- q²: homozygous recessive genotype (aa)
This results in the equation:
- p² + 2pq + q² = 1
Applications of the Hardy-Weinberg Equilibrium include estimating carrier frequencies for genetic diseases and detecting any evolutionary forces acting on populations, as deviations from expected frequencies indicate that one or more conditions for equilibrium are not satisfied, suggesting evolution is occurring.
Youtube Videos

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Principle Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Hardy-Weinberg Principle provides a mathematical model to study genetic variation in a population under specific conditions. It states that allele and genotype frequencies will remain constant from generation to generation in the absence of evolutionary influences.
Detailed Explanation
The Hardy-Weinberg Principle is a fundamental concept in population genetics that helps scientists understand how genetic variation remains stable in a population over time. This principle assumes that if certain conditions are met, the frequencies of different alleles will not change from one generation to the next. This stability occurs when there are no external forces such as mutations, migrations, or natural selection affecting allele frequencies. Understanding this principle allows researchers to identify when and how populations may be evolving.
Examples & Analogies
Think of the Hardy-Weinberg Principle like a perfectly calm lake. In this scenario, if no wind or rain disturbs it, the surface of the water remains smooth and unchanged. Similarly, a population's genetic makeup stays stable and consistent when no evolutionary factors make waves in the genetic pool.
Conditions for Equilibrium
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a population to be in Hardy-Weinberg equilibrium, the following conditions must be met:
1. Large Population Size: Minimizes the impact of genetic drift.
2. Random Mating: No preference for specific genotypes.
3. No Mutation: Allele frequencies remain unchanged.
4. No Migration: No gene flow in or out of the population.
5. No Natural Selection: All genotypes have equal reproductive success.
Detailed Explanation
For a population to maintain Hardy-Weinberg equilibrium, five key conditions must be satisfied:
- Large Population Size: This helps reduce the effects of genetic drift, which is the random fluctuation of allele frequencies. In smaller populations, random events can have a more significant impact on genetic variation.
- Random Mating: Individuals in the population must mate without preference for any particular trait. This ensures that all genotypes are equally likely to reproduce.
- No Mutation: New alleles must not be introduced or change existing alleles in the gene pool. This stability is crucial for maintaining allele frequencies.
- No Migration: If individuals move in or out of the population, they can bring new alleles with them or remove existing ones, disrupting the equilibrium.
- No Natural Selection: All genotypes must have equal chances of survival and reproduction. If certain genotypes have an advantage, it will cause a shift in allele frequencies over time.
Together, these conditions create a stable environment in which the genetic structure of the population remains unchanged.
Examples & Analogies
Consider a game of cards where every player has an equal hand size, and they draw cards randomly from a balanced deck. If all players draw from the same deck without modifications (no adding or removing cards), and everyone has the same chance to play, the distribution of cards in hand stays consistent round after round. Likewise, a population remains in Hardy-Weinberg equilibrium when these five conditions are met, ensuring an unaltered genetic distribution.
Hardy-Weinberg Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a gene with two alleles, A (dominant) and a (recessive):
- Let p represent the frequency of allele A.
- Let q represent the frequency of allele a.
Since there are only two alleles:
p + q = 1
The genotype frequencies can be predicted using:
p² + 2pq + q² = 1
Where:
- p²: Frequency of homozygous dominant genotype (AA).
- 2pq: Frequency of heterozygous genotype (Aa).
- q²: Frequency of homozygous recessive genotype (aa).
Detailed Explanation
The Hardy-Weinberg equations allow scientists to calculate the expected frequencies of genotypes in a population based on the frequencies of the alleles. If we consider a gene with two alleles, A and a:
- Allele Frequencies: Let 'p' be the frequency of the dominant allele (A), and 'q' be the frequency of the recessive allele (a). Importantly, because these are the only two possibilities, their frequencies must add up to 1, or 100%: p + q = 1.
- Genotype Frequencies: Using allele frequencies, we can predict the proportion of genotypes in the population:
- p² represents the frequency of homozygous dominant individuals (AA).
- 2pq represents the frequency of heterozygous individuals (Aa).
- q² represents the frequency of homozygous recessive individuals (aa).
This predictive power helps estimate genetic diversity and provides insights into potential evolutionary processes occurring in the population.
Examples & Analogies
Imagine a bag full of colored marbles where 'A' is represented by red marbles and 'a' by blue marbles. If you determine that 80% of the marbles are red (p=0.8) and 20% are blue (q=0.2), you can use the equations to forecast how many marble combinations you would have in a handful of marbles drawn from that bag. By using p², 2pq, and q², you can visualize and predict how many of each color combination would appear, similar to how scientists can predict genotype frequencies in a population.
Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
● Estimating Carrier Frequencies: Useful in predicting the number of carriers for genetic diseases.
● Detecting Evolutionary Forces: Deviations from expected frequencies suggest that one or more Hardy-Weinberg conditions are not met, indicating evolutionary change.
Detailed Explanation
The Hardy-Weinberg Principle is not only a theoretical model but has practical applications as well:
1. Estimating Carrier Frequencies: This principle can help estimate the frequency of carriers for specific genetic diseases in a population. By understanding allele frequencies, researchers can predict how many individuals might carry a recessive allele that could result in a genetic disorder if two carriers reproduce.
2. Detecting Evolutionary Forces: Scientists utilize Hardy-Weinberg equations to compare observed genetic data from populations against expected frequencies. When there are significant deviations from these expectations, it often indicates that one or more of the Hardy-Weinberg assumptions are being violated—such as the presence of natural selection, genetic drift, or mutations—signifying that evolution is taking place.
Examples & Analogies
Think of a school where the administration keeps track of students’ grades. By looking at expected grades based on past performance (akin to Hardy-Weinberg expectations), if too many students fail, the administration will know that something is wrong—possibly due to new teaching methods or external pressures. Similarly, deviations from Hardy-Weinberg expectations indicate that external factors are influencing genetic makeup, leading to evolutionary shifts.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hardy-Weinberg Principle: A mathematical model predicting stable allele and genotype frequencies under ideal conditions.
-
Conditions for Equilibrium: Large population, random mating, no mutations, no migration, and no natural selection.
-
Allele Frequency: The proportion of a specific allele in a population's gene pool.
-
Genotype Frequency: The proportion of different genotypes in the population, calculated using Hardy-Weinberg equations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a population of 100 individuals where there are 80 A alleles and 20 a alleles, the allelic frequencies would be p = 0.8 and q = 0.2. Using Hardy-Weinberg equations, we can predict the genotype frequencies.
-
If a population deviates from Hardy-Weinberg expected frequencies, this may indicate influences such as natural selection or genetic drift.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a population so grand, with genes hand in hand, allele frequencies stay, as long as conditions play.
📖 Fascinating Stories
-
Once in a quiet village, all alleles lived side by side in harmony. They promised that if they avoided migration, mutation, and selection, their frequencies would remain steadfast.
🧠 Other Memory Gems
-
Remember: 'Loving Monkeys Mingle Sweetly Near Trees' for Large Population, Random Mating, No Mutation, No Migration, No Natural Selection.
🎯 Super Acronyms
HWE
- Hardy-Weinberg Equilibrium denotes all genes of a bird's population with even qualities.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Gene Pool
Definition:
The total set of genetic information within an interbreeding population.
-
Term: Allele Frequency
Definition:
The relative frequency of an allele at a genetic locus in a population.
-
Term: HardyWeinberg Equilibrium
Definition:
A condition under which allele and genotype frequencies remain constant in a population across generations in the absence of evolutionary influences.
-
Term: Natural Selection
Definition:
The process by which traits that enhance survival and reproduction become more common in a population.
-
Term: Genetic Drift
Definition:
Random changes in allele frequencies that occur in small populations.

