Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Trigonometric Identities
Unlock Audio Lesson
Today, we're diving into trigonometric identities. Can anyone tell me what they think an identity is in mathematics?
I think it’s an equation that is always true!
Exactly! So, trigonometric identities are equations that involve sine, cosine, and other trigonometric functions that hold true for all angles. One of the most important is the Pythagorean identity, which states that sin²θ + cos²θ = 1. Who can remember what this implies?
It means you can use it to find one function if you have the other!
Right! This relationship is powerful because it allows us to switch between sine and cosine easily!
Can we see another example of an identity?
Certainly! Let’s look at the identity: 1 + tan²θ = sec²θ. This also connects the tangent and secant functions. What do you think this tells us?
It shows how tangent is related to secant, right?
Exactly! And understanding these relationships helps in solving problems involving trigonometric functions. Now, let’s wrap up: remembering these identities will make solving trigonometric equations much easier.
Verifying Trigonometric Identities
Unlock Audio Lesson
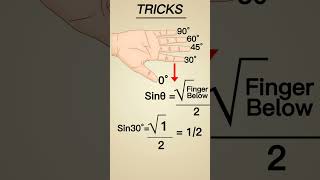
Now, let’s take an identity and verify it. For example, we’ll check if 1 + tan²45° = sec²45°. Can anyone tell me what tan45° equals?
Tan 45° is 1!
Great! Now, let’s plug that in. What does the left side of the equation become?
1 + 1² = 2, so the left side is 2.
Correct! Now, what about the right side? What does sec45° equal?
Uh, sec 45° is √2.
Right! And what happens when you square that?
It becomes 2!
Exactly! Since both sides equal 2, we’ve verified our identity. It's important to practice these verifications. Who can summarize what we did?
We substituted values into both sides of the equation and confirmed they were equal!
Well summarized! Keep practicing and verifying identities will become second nature.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers key trigonometric identities, including the Pythagorean identity, tangent and secant identities, and cotangent and cosecant identities. It illustrates their significance by providing an example of verifying an identity step-by-step, highlighting their application in solving trigonometric equations.
Detailed
In this section, we explore trigonometric identities, essential equations that establish relationships among the various trigonometric functions. The most fundamental identity is the Pythagorean identity, represented as sin²θ + cos²θ = 1, which forms the basis for deriving other identities. We also examine the relationships involving tangent and secant functions (1 + tan²θ = sec²θ) and cotangent and cosecant functions (1 + cot²θ = csc²θ). An illustrative example demonstrating how to verify a specific identity highlights procedural strategies in tackling trigonometric identities. Understanding these identities is crucial for simplifying expressions and solving equations in trigonometry.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fundamental Trigonometric Identities
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fundamental identities include:
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = csc²θ
Detailed Explanation
Trigonometric identities are equations that involve trigonometric functions and are true for all values of the variables involved. The three fundamental identities mentioned in this chunk are cornerstones of trigonometry:
1. sin²θ + cos²θ = 1: This states that for any angle θ, the square of the sine of the angle plus the square of the cosine of the angle equals one.
2. 1 + tan²θ = sec²θ: This identity shows the relationship between the tangent and the secant functions, indicating that the square of the tangent of an angle plus one equals the square of the secant of the angle.
3. 1 + cot²θ = csc²θ: This relates the cotangent and cosecant functions similarly, demonstrating that the square of the cotangent plus one equals the square of the cosecant.
These identities can be used to simplify expressions and solve equations that involve trigonometric functions.
Examples & Analogies
Imagine you're building a ramp to connect a sidewalk to a pathway. To ensure the ramp is stable, you need to maintain certain angles and heights. The fundamental identities are like the rules you follow to make sure your ramp works correctly at various angles, ensuring smooth transitions and proper support no matter how steep the ramp is.
Verifying Trigonometric Identities
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example:
Verify the identity 1 + tan²45° = sec²45°.
Solution:
- tan 45° = 1 ⇒ 1 + 1² = 1 + 1 = 2
- sec 45° = 1/cos 45° = 1/(√2/2) = √2
- sec²45° = (√2)² = 2
Thus, LHS = RHS = 2, hence identity verified.
Detailed Explanation
In this example, we are asked to verify the identity involving the angle 45 degrees. Here's how we break it down:
1. Calculating tan 45°: We know that the tangent of 45 degrees is 1. Putting this into our equation gives us 1 + 1² which simplifies to 2.
2. Calculating sec 45°: The secant of 45 degrees is calculated by taking the reciprocal of the cosine of 45 degrees. Since cos 45° = √2/2, then sec 45° = 1/(√2/2) = √2. Squaring sec 45° gives us 2.
3. By showing that both sides of the equation equal 2, we effectively verified that our original identity is correct.
This process is crucial in trigonometry to trust the relationships between various trigonometric functions.
Examples & Analogies
Think of verifying a recipe. When baking, you measure ingredients according to the recipe. If you mix probably measured flour and sugar, and the end result tastes just right, you've verified the recipe holds true. Similarly, by showing that both sides of a trigonometric identity yield the same result, we confirm that the mathematical 'recipe' works perfectly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pythagorean Identity: sin²θ + cos²θ = 1 shows the basic relationship between sine and cosine.
-
Tangent Identity: 1 + tan²θ = sec²θ links the tangent function to secant.
-
Cotangent Identity: 1 + cot²θ = csc²θ connects cotangent with cosecant.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Verify the identity 1 + tan²45° = sec²45° using tan45° = 1.
-
Use the Pythagorean identity sin²θ + cos²θ = 1 to find one function if the other is known.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Sine and cosine, a perfect team, add their squares to form the dream!
📖 Fascinating Stories
-
In a right triangle, the square of sine and cosine held a secret bond—together they always sum up to one, making every right-angled triangle fun!
🧠 Other Memory Gems
-
SCAT for remembering sin² + cos² = 1: Sine, Cosine, Always Together.
🎯 Super Acronyms
PTC for Pythagorean Trigonometric Constants
- P: for Pythagorean
- T: for Tangent
- C: for Cotangent.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Trigonometric Identities
Definition:
Equations that hold true for all angles involving trigonometric functions.
-
Term: Pythagorean Identity
Definition:
The equation sin²θ + cos²θ = 1, relating sine and cosine functions.
-
Term: Tangent Identity
Definition:
The identity 1 + tan²θ = sec²θ, linking tangent and secant functions.
-
Term: Cotangent Identity
Definition:
The identity 1 + cot²θ = csc²θ, relating cotangent and cosecant functions.