Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Faraday's First Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to dive into Faraday's First Law of Induction. It states that a change in the magnetic field within a closed loop induces an electromotive force, or EMF, in the conductor. Can anyone explain what we mean by 'magnetic flux'?
Is it the amount of magnetic field passing through the loop?
Exactly! The magnetic flux is essentially the product of the magnetic field and the area of the loop. Remember, it’s important to understand that changes in this flux are what induce EMF. Can anyone tell me what the mathematical formula for this looks like?
It's E = -dΦB/dt, right?
That's correct! The E represents the induced EMF. The negative sign comes from Lenz’s Law, which indicates that the direction of induced EMF opposes the change. Why do you think this is important?
It could prevent unexpected changes in the electrical circuit?
Great point! It helps maintain energy conservation. Now, can anyone summarize what we talked about regarding Faraday’s First Law?
Changes in magnetic flux cause an induced EMF that opposes that change.
Wonderful summary! Let's keep this idea of opposing changes in mind as we proceed.
Exploring Faraday's Second Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's move on to Faraday's Second Law. This law tells us that the magnitude of the induced EMF is proportional to the rate of change of the magnetic flux. Who can tell me how we could increase the induced EMF?
By increasing how quickly the magnetic field changes!
Correct! We can also increase the induced EMF by adding more loops of wire in our coil. Any thoughts on why that works?
More loops mean more magnetic flux interacting with the wire.
Exactly! Also, using a stronger magnet can enhance the EMF. Can someone remind us what the implications of these laws are in real-world applications?
They are used in generators, right?
Correct again! Generators rely on these principles to convert mechanical energy into electrical energy. As we wrap up, why is understanding these laws crucial in engineering?
It helps design efficient electrical devices.
Excellent! Keep thinking about how we can apply this knowledge.
Application and Implications of Induction Laws
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s explore some applications of Faraday’s Laws. One common example is electric generators. Who can explain how a generator uses these principles?
A generator rotates a coil in a magnetic field, changing the magnetic flux.
Exactly! This rotation induces an EMF due to the changing magnetic flux. Can anyone think of other devices that may utilize Faraday's Laws?
Transformers use electromagnetic induction too!
Correct! Transformers step up or step down voltage using coils and changing magnetic fields. So, how does understanding these laws impact our lives today?
It shows how we convert energy and transport it effectively.
Exactly, understanding these principles allows us to develop better energy solutions. Can anyone summarize the applications of Faraday’s laws we discussed?
They are used in generators, transformers, and other electrical devices.
Great job! Understanding these laws unlocks many technological advancements.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines Faraday's two laws of electromagnetic induction, which state that a change in magnetic flux induces an EMF and that the magnitude of the induced EMF is proportional to the rate of change of magnetic flux. It emphasizes the importance of these laws in various electrical applications.
Detailed
Faraday's Laws of Electromagnetic Induction
Overview
Faraday’s laws of electromagnetic induction explain the relationship between changing magnetic fields and the generation of electromotive force (EMF) in conductors. These foundational principles help in understanding electrical technologies such as generators and transformers.
Faraday's First Law
- Statement: A change in the magnetic field within a closed loop induces an EMF in the conductor.
- Mathematical Expression:
\[ E = - \frac{d\Phi_B}{dt} \]
where:
- E is the induced EMF (Volts)
- Φ_B is the magnetic flux through the loop
- t is time
- The negative sign reflects Lenz's Law, which dictates that the induced EMF opposes the change in magnetic flux.
Faraday's Second Law
- Statement: The magnitude of induced EMF is proportional to the rate at which magnetic flux changes. This can be enhanced by:
- Increasing the rate of change of magnetic flux.
- Adding more loops to the coil.
- Using a stronger magnet.
In conclusion, Faraday's laws form the backbone of electromagnetic induction, influencing a wide range of applications in electrical engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Faraday’s First Law of Induction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
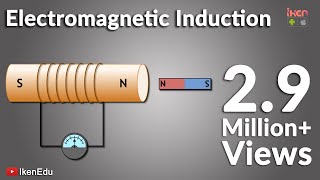
Faraday’s First Law states that a change in the magnetic field within a closed loop induces an electromotive force (EMF) in the conductor forming the loop.
Mathematically, it is expressed as:
E=−dΦBdt
where:
○ E is the induced EMF (in Volts),
○ ΦB is the magnetic flux through the loop,
○ t is time.
The negative sign in the equation indicates the direction of the induced EMF, which opposes the change in magnetic flux, as per Lenz's Law (discussed later).
Detailed Explanation
Faraday's First Law of Induction explains that when there is a change in the magnetic field inside a closed loop of wire, an electromotive force (EMF) is created. This is like how pushing a swing causes it to move—the change causes a reaction. The formula, E = -dΦB/dt, conveys that the induced EMF (E) depends on how quickly the magnetic flux (ΦB) changes over time (t). The negative sign means that the EMF created works against the change, which keeps the system stable—this is linked to Lenz's Law, which we'll cover later, emphasizing conservation of energy.
Examples & Analogies
Imagine you're at the beach holding a beach ball under water. As you push down the ball (a change in position), it pushes back against your hand. This is similar to how Faraday's First Law works—when you change the magnetic field inside a loop, it induces a current that 'pushes back' against that change.
Faraday’s Second Law of Induction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Faraday’s Second Law states that the magnitude of the induced EMF is proportional to the rate of change of the magnetic flux.
The induced EMF can be increased by:
○ Increasing the rate of change of the magnetic flux,
○ Increasing the number of loops in the coil (if the coil is wound),
○ Using a stronger magnet.
Detailed Explanation
Faraday's Second Law tells us that how much EMF is induced depends on how fast the magnetic flux changes. If you change the magnetic field very quickly, more EMF will be generated. You can also increase the induced EMF by adding more loops of wire in the coil so more magnetic flux is captured, or by using a stronger magnet that changes the field more intensely. Think of it as the difference between pushing a swing gently and pushing it hard; the harder push (sudden change) generates a bigger response (higher EMF).
Examples & Analogies
Consider a bicycle dynamo that generates electricity when you pedal. If you pedal faster (increasing the rate of change), the light shines brighter. Similarly, if the dynamo had more coils or we used a super magnet, the light would also shine brighter. It’s all about how quickly and effectively we change the magnetic environment around the coils.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Faraday's First Law: A change in magnetic flux induces an EMF in a conductor.
-
Faraday's Second Law: The induced EMF is proportional to the rate of change of magnetic flux.
-
Lenz's Law: The induced EMF opposes the change that caused it.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A coil rotating in a magnetic field induces current in a generator.
-
Transformers use changing magnetic fields to adjust voltage across coils.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If the field's changing, the EMF is there; Faraday's laws, they've got the flair!
📖 Fascinating Stories
-
Imagine a loop in a river representing magnetic flux; as the water’s speed changes, so does the current in our loop, illustrating Faraday's principles!
🧠 Other Memory Gems
-
Remember 'FLIP' for Faraday's Laws: Flux change leads to Induced EMF, with direction opposing what you have.
🎯 Super Acronyms
FIE - Faraday's Induction Effect.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Electromotive Force (EMF)
Definition:
The voltage generated by a changing magnetic field or an electric current.
-
Term: Magnetic Flux (Φ_B)
Definition:
The product of the magnetic field and the area through which the field lines pass.
-
Term: Lenz's Law
Definition:
A principle stating that the direction of induced EMF opposes the change in magnetic flux.