Functions
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of a Function
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're diving into the concept of functions. A function is a special type of relation where each element from the domain corresponds to exactly one element in the co-domain. Can anyone tell me what we mean by domain and co-domain?

Is the domain the set of all possible inputs?

Exactly! And what about the co-domain?

That's the set from which the outputs come, right?

Great job! So if we have a function `f: A → B`, we can say that `f` associates each element `x` in `A` with exactly one element `y` in `B`, denoted as `f(x) = y`. Let’s move on to the types of functions.
Types of Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Functions can be categorized in different ways. First, we have injective functions, or one-to-one functions. What do you think makes a function injective?

I think it's when every element in the domain maps to a unique element in the co-domain.

Exactly! Now, can someone differentiate it from a surjective function?

A surjective function means every element in the co-domain must be mapped to at least once by the domain.

Right again! And do you remember what we call a function that is both injective and surjective?

That would be a bijective function!

Excellent! Now let's summarize what we’ve learned about types of functions.
Domain, Co-domain, and Range
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss domain, co-domain, and range in more detail. Can someone explain the difference between co-domain and range?

The co-domain is the set of potential outputs, while the range is the actual outputs we get when we apply the function.

Exactly! For example, if `f: A → B` and `A = {1, 2, 3}` and `f` maps them to `B = {a, b, c}`, but it only outputs `{a, b}`, `{a, b}` is the range. Why is understanding this important?

It helps us know how functions behave and the uniqueness of outputs!

Exactly! Understanding the concepts of domain, co-domain, and range prepares us for more complex operations with functions.
Composition of Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, we have the composition of functions. Who can tell me what it means to compose two functions?

It’s like using the output of one function as the input for another?

Correct! We write it as `g∘f`, which means 'g of f'. For example, if we have `f: A → B` and `g: B → C`, then `g∘f: A → C`. Can anyone give me a practical example of this?

If `f` converts temperatures from Celsius to Fahrenheit, and `g` converts Fahrenheit to Kelvin, you can find Kelvin by composing those functions!

Excellent example! Composition is very powerful in functions.
Inverse of Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s talk about the inverse of a function. What do you think it means for a function to have an inverse?

I think it means you can reverse the operations of that function.

Exactly! A function `f: A → B` has an inverse `f⁻¹: B → A` if `f(f⁻¹(y)) = y` for every `y` in the range of `f`. When do we know a function has an inverse?

When it's bijective, right?

Correct again! A bijective function ensures each output has one input, allowing for reversal. Let’s summarize our discussion today.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section on functions outlines the definition of a function as a specific type of relation, elaborates on various types of functions, including injective, surjective, and bijective, and explains terms such as domain, co-domain, and range. Additionally, it introduces composition of functions and the concept of an inverse function.
Detailed
Functions in Mathematics
In this section, we explore the concept of functions, which are fundamental to understanding relationships in mathematics. A function can be seen as a special type of relation where each element in the domain corresponds to exactly one element in the co-domain, denoted by the notation f: A → B.In a function, one input gives exactly one output. In a general relation, an input may give multiple outputs.
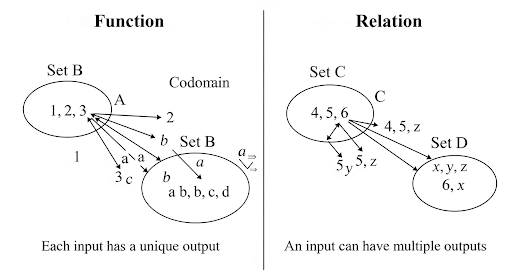
Key Concepts:
- Domain: The complete set of possible inputs for the function.
- Co-domain: The set that contains all possible outputs that the function may return.
- Range: The actual outputs produced by the function from the given inputs.
Types of Functions:
- One-to-One Function (Injective): A function where every element in the domain maps to a unique element in the co-domain.
- Onto Function (Surjective): A function where every element in the co-domain has at least one corresponding element in the domain.
- One-to-One Correspondence (Bijective): A function that is both injective and surjective.
We also study the composition of functions and inverses. The composition of two functions, denoted as g∘f, is defined as applying function f first and then applying function g. Inverse functions reverse the effect of a function, where a function has an inverse if it is bijective. Understanding functions lays a critical foundation for advanced mathematical concepts.
Q. Match the following:
| Function Type | Condition / Property |
|---|---|
| 1. One-one (Injective) | a. If $f(x_1) = f(x_2) \implies x_1 = x_2$ |
| 2. Onto (Surjective) | b. Every element of the codomain has a pre-image in the domain |
| 3. Many-one | c. If $f(x) = f(y)$ does not always imply $x = y$ |
| 4. Constant Function | d. Maps every element of the domain to the same value |
| 5. Identity Function | e. $f(x) = x$ |
| 6. Polynomial Function | f. $f(x) = ax + b$, with $a \neq 0$ |
| 7. Exponential Function | g. Of the form $f(x) = e^x$ or $a^x, a>0, a\neq1$ |
| 8. Trigonometric Function | h. Periodic in nature, e.g. $f(x) = \sin x, \cos x$ |
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Function
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A function is a special type of relation where each element of the domain (set 𝐴) is related to exactly one element of the co-domain (set 𝐵).
If 𝑓 is a function from set 𝐴 to set 𝐵, then we write it as:
𝑓:𝐴 → 𝐵
A function associates each element 𝑥 ∈ 𝐴 to a unique element 𝑦 ∈ 𝐵, denoted as 𝑓(𝑥) = 𝑦.
Example:
If 𝐴 = {1,2,3} and 𝐵 = {𝑎,𝑏,𝑐}, a function 𝑓 might be:
𝑓 = {(1,𝑎),(2,𝑏),(3,𝑐)}
Detailed Explanation
A function is a specific kind of relation. In a simple sense, it means that for every input, there is one and only one output. Think of the domain as a set of values you can choose from (Set A) and the co-domain as a set where the output can be found (Set B). When we say that f is a function from set A to set B, we look for a consistent relationship where each element from A pairs with exactly one element from B. For example, if we have 1 mapped to 'a', then there's no way to map 1 to another value like 'b' in function f. This is what distinguishes functions from general relations, where one input could relate to multiple outputs.
Examples & Analogies
Imagine a vending machine where you enter a specific button (your input) and receive a specific snack (your output). If you press the button for 'C', you will always get a chocolate bar. This is like a function – pressing 'C' (input) will always give you 'chocolate' (output). You can't press 'C' and get a cookie at the same time, which illustrates that each input corresponds to one unique output.
Types of Functions
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
-
One-to-One Function (Injective Function):
A function is one-to-one (injective) if different elements of the domain are mapped to different elements in the co-domain.
Example: If 𝑓 = {(1,𝑎),(2,𝑏),(3,𝑐)}, the function is injective because each element in 𝐴 maps to a unique element in 𝐵. -
Onto Function (Surjective Function):
A function is onto (surjective) if every element of the co-domain is mapped to by at least one element from the domain.
Example: If 𝑓 = {(1,𝑎),(2,𝑏),(3,𝑏)}, the function is surjective because every element of 𝐵 has at least one corresponding element in 𝐴. -
One-to-One Correspondence (Bijective Function):
A function is bijective if it is both one-to-one (injective) and onto (surjective).
Example: If 𝑓 = {(1,𝑎),(2,𝑏),(3,𝑐)}, the function is bijective because it is both injective and surjective.
Detailed Explanation
Functions come in different types based on how they relate elements from the domain to the co-domain. There are three primary types:
1. One-to-One Functions ensure that every input corresponds to a unique output; like having a unique parking space for each car – no two cars can park in the same space.
2. Onto Functions guarantee that every possible output in the co-domain has at least one input from the domain; think of a classroom where every student (input) is assigned to a desk (output) ensuring no desk is left empty.
3. Bijective Functions combine the attributes of both types: they are unique and cover the entire co-domain – like a perfect matching in a dance where every dancer finds a partner and no partners remain unpaired.
Examples & Analogies
Consider an online store:
- The one-to-one function is like a scenario where each type of product can only be purchased once at a time. If a buyer clicks to buy a product, that product removes the same option for others.
- The onto function would imply that every item in the store is bought at least once by some customer, making sure every available item is appreciated.
- Finally, a bijective function represents when every unique product has a dedicated buyer, meaning every product is sold and every buyer buys only one item, a perfect transaction.
Domain, Co-domain, and Range
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Domain: The set of all possible input values for a function.
• Co-domain: The set of possible output values for the function.
• Range: The set of actual output values of the function.
For example, in the function 𝑓:𝐴 → 𝐵, the domain is 𝐴, the co-domain is 𝐵, and the range is the set of values that 𝑓 maps to in 𝐵.
Detailed Explanation
In the context of functions, we need to distinguish three key terms:
- Domain refers to all the inputs from which a function can draw. In simpler terms, it’s like the selection of fruits you can choose when making a fruit salad.
- Co-domain is broader; it includes all potential outputs a function could theoretically yield. Continuing the fruit salad analogy, this could be all types of salads that can be made, even those not made with your selected fruits.
- Range is the actual set of outputs that the function produces when you apply it to the domain. It narrows down to the specific salads created from the fruits you've chosen. Thus, while the co-domain sets the possibilities, the range reveals what has truly been achieved based on your inputs.
Examples & Analogies
Think of a restaurant:
- The domain is like the menu items you can order, the variety of foods (input values) available to you.
- The co-domain includes every type of food that can theoretically be offered based on what the restaurant could stock.
- The range is what you actually find on your table after ordering, representing the dishes delivered based on your choices – only what you ordered and what the kitchen was able to prepare.
Key Concepts
-
Domain: The complete set of possible inputs for the function.
-
Co-domain: The set that contains all possible outputs that the function may return.
-
Range: The actual outputs produced by the function from the given inputs.
-
Types of Functions:
-
One-to-One Function (Injective): A function where every element in the domain maps to a unique element in the co-domain.
-
Onto Function (Surjective): A function where every element in the co-domain has at least one corresponding element in the domain.
-
One-to-One Correspondence (Bijective): A function that is both injective and surjective.
-
We also study the composition of functions and inverses. The composition of two functions, denoted as
g∘f, is defined as applying functionffirst and then applying functiong. Inverse functions reverse the effect of a function, where a function has an inverse if it is bijective. Understanding functions lays a critical foundation for advanced mathematical concepts. -
Q. Match the following:
-
| Function Type | Condition / Property |
-
| ------------------------- | -------------------------------------------------------------- |
-
| 1. One-one (Injective) | a. If $f(x_1) = f(x_2) \implies x_1 = x_2$ |
-
| 2. Onto (Surjective) | b. Every element of the codomain has a pre-image in the domain |
-
| 3. Many-one | c. If $f(x) = f(y)$ does not always imply $x = y$ |
-
| 4. Constant Function | d. Maps every element of the domain to the same value |
-
| 5. Identity Function | e. $f(x) = x$ |
-
| 6. Polynomial Function | f. $f(x) = ax + b$, with $a \neq 0$ |
-
| 7. Exponential Function | g. Of the form $f(x) = e^x$ or $a^x, a>0, a\neq1$ |
-
| 8. Trigonometric Function | h. Periodic in nature, e.g. $f(x) = \sin x, \cos x$ |
Examples & Applications
Example of a Function: Let A = {1, 2, 3} and B = {a, b, c}; let f = {(1, a), (2, b), (3, c)}. Here, f is a function.
Injective Function Example: f = {(1, a), (2, b), (3, c)} is injective because all elements map uniquely.
Surjective Function Example: f = {(1, a), (2, b), (3, b)} is surjective as both b's from the co-domain have matching elements.
Bijective Function Example: f = {(1, a), (2, b), (3, c)} is bijective since it is both injective and surjective.
Composition Example: If f: A → B and g: B → C, then g∘f: A → C means first apply f then g.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a function, each input's a friend, mapping to one output ‘til the end.
Stories
Imagine a postmaster who delivers letters. Each address (input) gets one letter (output) without mix-ups, ensuring that no address ends up with two letters—this is a function!
Memory Tools
F-D-C: Function, Domain, Co-domain. Remember that each Function has its unique Domain and Co-domain.
Acronyms
I-S-B
Injective
Surjective
Bijective. A quick way to remember main function types!
Flash Cards
Glossary
- Function
A relation where each element of the domain is related to exactly one element of the co-domain.
- Domain
The set of all possible input values for a function.
- Codomain
The set of potential outputs for a function.
- Range
The set of actual output values from a function.
- Injective Function (OnetoOne)
A function where each element in the domain maps to a unique element in the co-domain.
- Surjective Function (Onto)
A function where every element in the co-domain has at least one element in the domain mapping to it.
- Bijective Function
A function that is both injective and surjective.
- Composition of Functions
A method of combining two functions where the output of one function becomes the input of another.
- Inverse of a Function
A function that 'reverses' another function's operation.
Reference links
Supplementary resources to enhance your learning experience.
