Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Degree of Freedom (DOF)
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're going to explore the concept of Degree of Freedom, often abbreviated as DOF. Can anyone tell me what this means?
Does it refer to how much a mechanical system can move?
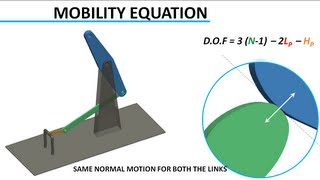
Exactly! The DOF refers to the minimum number of independent parameters needed to define the configuration of a mechanism completely. For planar mechanisms, we express this using GrΓΌblerβs Formula: F = 3(n-1) - 2jβ - jβ.
What do n, jβ, and jβ represent?
Great question! Here, 'n' is the total number of links including the frame, 'jβ' is the number of lower pairs, and 'jβ' represents the higher pairs. Remember these terms with the acronym **LoHa**: **L**inks, **H**igher pairs, **A**nd lower pairs.
So, if a mechanism has 4 links and 1 lower pair, how would I calculate the DOF?
You would plug those values into the formula. With n = 4 and jβ = 1, the equation becomes F = 3(4-1) - 2(1) - 0, which gives you a DOF of 7.
Got it! The more pairs you have, the lower the DOF, right?
Precisely! Lower pairs restrict movement more than higher pairs. Let's recap: DOF is critical for analyzing mechanisms, and we use the formula to determine how they can operate.
Grashofβs Rule
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand DOF, letβs talk about Grashofβs Rule, which helps determine if a four-bar linkage can rotate fully. Any ideas what it states?
It has to deal with the lengths of the links, right?
Yes! The rule states that if s + l β€ p + q, where s is the shortest link and l is the longest, at least one link can make a complete rotationβthis makes it a Grashof-type mechanism.
But if the condition is false, then what happens?
Good observation! If the condition isnβt satisfied, we have a non-Grashof type mechanism where no link can complete a full rotation.
Can you give us an example of such mechanisms?
Certainly! Think of a standard two-link slider-crank mechanism versus a complicated linkage like a car suspension system. Each has different link lengths affecting their motion. Remember, the output links' ability to rotate fully is contingent on this criterion.
Perfect! So, analyzing the link lengths can tell us a lot about the mechanism's capability.
Exactly! Great job grasping the importance of Grashofβs Rule in mechanism design.
Mechanical Advantage and Transmission Angle
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next up, weβll discuss Mechanical Advantage, or MA. Can anyone explain what it represents?
Isnβt it how much input force is transformed into output force?
Exactly! The formula is MA = Output Force / Input Force, or alternatively, MA = Velocity of input / Velocity of output. A higher MA indicates greater force amplification. Remember, mechanical advantage is crucial for understanding efficiency!
Does that mean it varies throughout the motion?
Correct! It varies based on the configuration during the cycle. Letβs now pivot to the transmission angle. Who can tell me what this angle is?
It's the angle between the output link and the coupler link in four-bar mechanisms, right?
Exactly, and ideally, this angle should be between 45Β° and 135Β° for effective force transmission. If itβs smaller, it can lead to mechanical inefficiencies.
Why is that?
Because a smaller angle causes large forces with little motion, making the mechanism inefficient. So remember, aim for that ideal range for optimal performance!
To sum up, both MA and transmission angle are fundamental to understand how mechanisms work!
Right on! Understanding these concepts will help in designing efficient mechanisms.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
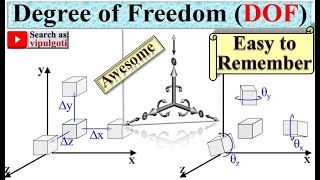
The Degree of Freedom (DOF) indicates the number of independent parameters necessary to define a mechanism's configuration. It encompasses concepts like planar mechanisms, Grashof's Rule for rotatability in linkages, mechanical advantage, and transmission angles, providing a comprehensive understanding of how mechanisms function.
Detailed
Degree of Freedom (DOF)
The degree of freedom of a mechanism is critical in understanding its kinematic behavior. It refers to the minimum number of independent parameters (usually displacements) that are needed to completely define the system's configuration. For planar mechanisms, this is determined by GrΓΌblerβs Formula, given by F=3(nβ1)β2jββjβ, where:
- F: Degree of freedom
- n: Number of links, including the frame
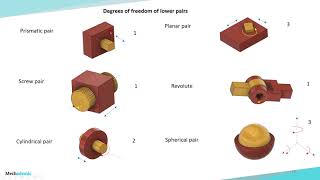
- jβ: Number of lower pairs (single DOF joints like revolute or prismatic)
- jβ: Number of higher pairs (like cams or gears)
This formula is essential for analyzing how many motions or actions can occur within a given mechanism.
Grashofβs Rule
Grashof's criterion is essential for examining the rotatability of a four-bar linkage. The rule states that for lengths of the various links (shortest link s, longest link l, and two other links p and q), if the condition s+lβ€p+q is satisfied, at least one link can make a full rotation relative to another, making it a Grashof type mechanism.
Rotatability and Limit Positions
A rotatable link is one allowing a full 360Β° rotation. Conversely, limit positions refer to the extremes of motion beyond which the mechanism cannot operate.
Mechanical Advantage (MA)
Mechanical advantage is calculated by the equation MA=Output Force/Input Force or MA=Velocity of input/Velocity of output. A high mechanical advantage suggests enhanced force amplification but is dependent on the linkage configuration.
Transmission Angle (ΞΌ)
The transmission angle is the angle between the output and the coupler link in a four-bar mechanism. The ideal range for ΞΌ is 45Β° to 135Β° for effective force transmission. A smaller angle can lead to inefficiencies in mechanical design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Degree of Freedom
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The degree of freedom of a mechanism refers to the minimum number of independent parameters (usually displacements) required to define the configuration of the system completely.
Detailed Explanation
The degree of freedom (DOF) of a mechanism acts like a measure of its mobility. It tells us how many independent movements can occur in the system. For example, if you think of a robot arm, each joint can move independently, and depending on how many joints or links it has, you can determine its DOF. If a mechanism has a higher DOF, it can perform more complex motions.
Examples & Analogies
Imagine you are dancing. If you can only move your arms, your range of motion is limited (low DOF). However, if you can move your arms, legs, and torso independently, you can create more intricate dance moves (high DOF).
GrΓΌblerβs Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For planar mechanisms, DOF is given by:
F=3(nβ1)β2j1βj2
Where:
β FF: Degree of freedom
β nn: Number of links (including the frame)
β j1j_1: Number of lower pairs (single DOF joints like revolute or prismatic)
β j2j_2: Number of higher pairs (like cams, gears)
This equation is known as GrΓΌblerβs Formula.
Detailed Explanation
GrΓΌblerβs Formula provides a mathematical way to calculate the DOF for planar mechanisms. In the formula F = 3(n - 1) - 2j1 - j2:
- 'n' is the total number of links in the mechanism, including the frame.
- 'j1' counts the single-degree-of-freedom joints like revolute joints (which allow rotation) and prismatic joints (which allow sliding).
- 'j2' refers to higher pairs such as gears and cams, which don't allow simple translations or rotations. This formula helps engineers design mechanisms with the desired range of motion by incorporating the correct amount of links and joints.
Examples & Analogies
Think of this formula as a recipe. The number of links in a mechanism is like the number of ingredients you have. If you only have a few ingredients (links) but a lot of complex instructions (higher pairs), you might find it hard to create the dish you want (achieve the desired motion). This formula helps you balance ingredients and instructions to create something that is both functional and efficient.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
GrΓΌblerβs Formula: A key formula for calculating the DOF of planar mechanisms.
-
Grashof's Rule: A pivotal criterion for determining the rotatability of four-bar linkages based on the lengths of different links.
-
Mechanical Advantage: How a mechanism can amplify input forces to produce output forces, affected by configuration.
-
Transmission Angle: The angle that affects the efficiency of force transmission within a mechanism.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a four-bar linkage where the lengths satisfy Grashof's condition, allowing for efficient rotational motion.
-
Application of mechanical advantage in a simple lever, where the input force is amplified at the output.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In a mechanism, if DOF you seek, remember GrΓΌblerβs Formula, it's unique!
π Fascinating Stories
-
Once a mechanic had a mystical four-bar linkage. It could only rotate if it met the Grashof condition β short and long links must play nice, or the system would just roll the dice!
π§ Other Memory Gems
-
Remember RAM for Mechanical Advantage: Ratio, Amplification, Motion.
π― Super Acronyms
For transmission angle, remember FAST**
- F**orce
- **A**ngle
- **S**ystem
- **T**ransmission.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Degree of Freedom (DOF)
Definition:
The minimum number of independent parameters required to define the configuration of a mechanism completely.
-
Term: GrΓΌblers Formula
Definition:
The formula F = 3(n-1) - 2jβ - jβ used to determine the degree of freedom of planar mechanisms.
-
Term: Grashof's Rule
Definition:
A condition used to determine the rotatability of a four-bar linkage, governed by the lengths of the links.
-
Term: Mechanical Advantage (MA)
Definition:
The ratio of output force to input force, or the ratio of the velocity of input to output.
-
Term: Transmission Angle (ΞΌ)
Definition:
The angle between the output link and the coupler link in a four-bar mechanism.
-
Term: Lower Pair
Definition:
A joint that provides a single degree of freedom, such as a revolute or prismatic joint.
-
Term: Higher Pair
Definition:
A joint that has more than one degree of freedom, such as cams and gears.