Introduction to Column Buckling
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Column Buckling
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to dive into the concept of column buckling. Can anyone tell me what a column is in structural engineering?

It's a structural member that supports loads.

Exactly! And when subjected to axial compressive loads, a column can experience something known as buckling. This is a stability failure. What do you think that means?

Does it mean the column can bend and not break?

Correct! It bends under load even if the material itself isn’t yielding. Let's remember this with the acronym BEND: 'Buckling Even Not Deforming'—easy to recall, right?
Euler's Theory of Buckling
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, who can tell me about Euler's Theory of Buckling?

It tells us about the critical load when a column becomes unstable?

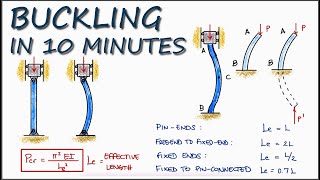
Good job! The formula is Pcr = π²EI/(Leff)². Does everyone recall what E and I stand for?

E is Young's modulus, and I is the moment of inertia.

Exactly! Young's modulus measures stiffness, and moment of inertia relates to the shape of the column’s cross-section. To help you remember, think of the phrase 'Elastic Intensity!'
Effective Lengths and Boundary Conditions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss how different boundary conditions affect effective lengths. Can anyone name a few types of end conditions?

Pinned-pinned and fixed-fixed?

Great examples! The effective lengths vary based on these conditions. The more stable the condition, the shorter the effective length, leading to higher resistance to buckling. Remember: Pinned is long, Fixed is short!
Limitations of Euler's Theory
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

What about limitations? Why should we be cautious using Euler’s formula?

It only works for long, slender columns?

Yes, it does! It also assumes straightness and ideal conditions. Let’s keep this in mind—picture a perfect, straight column like a pencil! If a column is imperfect, the reality can differ significantly.
Eccentric Loading
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s talk about eccentric loading. Who can explain what that is?

It's when the load isn't aligned with the center?

Exactly! This introduces bending stresses. Remember, 'Eccentric Equals Extra Stress', because columns under eccentric loads are more prone to failure. Always design with this in mind!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Column buckling occurs when a slender column bends under axial load, leading to stability failure. The section covers Euler's Theory, effective lengths depending on boundary conditions, and limitations of Euler's formula, illustrating the mechanics underlying column stability.
Detailed
In structural engineering, a column is defined as a member designed to carry axial compressive loads. Unlike typical material failure through yielding, buckling represents a stability failure where a slender column deforms unexpectedly under load, despite the material remaining elastic. This section details Euler’s Theory of Buckling, which calculates the critical load at which a perfectly straight, slender column becomes unstable: Pcr = π²EI/(Leff)², where E is Young's modulus, I is the moment of inertia, and Leff is the effective length, dependent on end conditions. Various boundary conditions affect the effective lengths, indicating that pinned, fixed, and free ends alter buckling resistance. Limitations of Euler's formula are significant, noting assumptions like homogeneity and validity only for long slender columns. Furthermore, eccentric loading raises complexity by introducing bending stresses, prompting design considerations for stability under combined axial and bending forces.
Youtube Videos





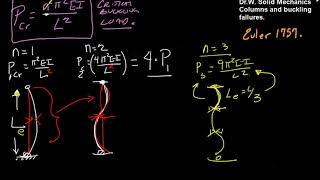
![[L28] Beam Theory – 8: Buckling – 3 (Example)](https://img.youtube.com/vi/kjsaKaaXHu8/mqdefault.jpg)

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Column
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A column is a structural member subjected to axial compressive loads.
Detailed Explanation
A column is defined as a vertical structural element that supports loads. In engineering, we refer to loads applied perpendicular to the height of the column as axial compressive loads. This type of loading tends to push the column downwards, and it's crucial for designers to know how much load a column can withstand without failing.
Examples & Analogies
Think of a column as a sturdy pillar holding up a ceiling. If we pile too many bricks on top of it (axial loads), we risk collapsing the pillar. The same principle applies to buildings where columns must be designed to handle certain loads.
Understanding Buckling
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Unlike failure by material yield, buckling is a stability failure that occurs when a slender column bends due to axial load, even if the material remains within elastic limits.
Detailed Explanation
Buckling is a unique type of failure distinct from the material yielding, which happens when materials deform beyond their strength limits. In contrast, buckling occurs when a slender column bends under load before reaching material failure. This failure is primarily a stability issue rather than a material strength problem, making it vital for engineers to consider the geometry as much as the material property when designing columns.
Examples & Analogies
Imagine a straight metal straw. If you push down on both ends, it bends (buckles) before it can break. This bending happens at a lower force than what would be needed to break the straw physically—demonstrating the concept of buckling.
Key Concepts
-
Column: A structural element supporting loads.
-
Buckling: Failure due to instability, not material yield.
-
Euler’s Theory: Computes critical load for buckling.
-
Effective Length: Length affecting stability based on boundary conditions.
-
Bending Stress: Stress introduced by eccentric loading.
Examples & Applications
A tall, slender steel column in a skyscraper is subject to axial load and may buckle under compressive forces.
A cantilever beam supporting a load at the end exhibits both axial and bending stress due to the non-axial nature of the load.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When a column stands tall and straight, load it gently, or it will fate, bend and buckle, won't break but create a state that's hard to take!
Stories
Imagine a narrow tower made of spaghetti. It stands proud until heavy books are stacked atop. The books press down until the tower bends at the top, showing how buckling sneaks in silently.
Memory Tools
Bumpy Columns Are Tough: B for Buckling, C for Columns, A for Axial loads, T for Tough.
Acronyms
BEND
Buckling Even Not Deforming represents how columns fail.
Flash Cards
Glossary
- Column
A structural member primarily designed to carry axial loads.
- Buckling
A stability failure characterized by bending without material yield.
- Euler’s Theory
A theory that provides the critical load formula for buckling.
- Effective Length
The length that a column behaves as if experiencing buckling, contingent on boundary conditions.
- Eccentric Loading
A load that is applied away from the centroid of a column, causing bending.
Reference links
Supplementary resources to enhance your learning experience.
