Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Beam Deflection
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, weβll explore the concept of beam deflection. Can anyone tell me why we need to measure deflection in beams?
To ensure they are safe and not sagging too much!
Exactly! Deflection impacts structural integrity and serviceability. It's crucial for avoiding excessive sagging. Remember, we use the equation $$\frac{d^2y}{dx^2} = \frac{M(x)}{EI}$$. Can someone explain what each term represents?
y is the deflection, M is the bending moment, E is Young's modulus, and I is the moment of inertia!
Great job! Keep in mind that understanding these relationships helps us model the behavior of beams under load.
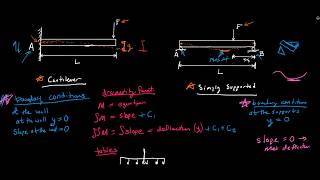
Double Integration Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs discuss how we can calculate deflection using the double integration method. What do we start with?
We start with the bending moment equation, right?
Exactly! Then we integrate to find the slope. Who remembers what we need to apply after integrating?
We need to apply boundary conditions!
Correct! Applying boundary conditions allows us to solve for the constants of integration. Very important!
Common Loading Cases
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs talk about some common loading cases. Who can tell me what the maximum deflection is for a cantilever with a point load at the free end?
Itβs $$\delta_{max} = \frac{PL^3}{3EI}$$!
Well done! And what about a simply supported beam with a central point load?
$$\delta_{max} = \frac{PL^3}{48EI}$$!
Exactly! Knowing these formulas helps us analyze the deflections efficiently.
Moment Area Theorem
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, letβs look at the Moment Area Method. Can someone explain what Theorem I states?
It says that the change in slope between two points is equal to the area under the M/EI diagram.
Exactly! And Theorem II relates to deflection. Can anyone summarize this theorem?
Deflection at a point relative to a tangent at another point equals the moment of the area under the M/EI diagram!
Perfect! This theorem simplifies our calculations, especially for piecewise loaded beams.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Beam deflection occurs when beams are subjected to transverse loads, and measuring this deflection is critical for ensuring structural safety and avoiding excessive sagging. Understanding the governing equations, methods of computation, and common loading cases is essential for engineers.
Detailed
Introduction to Beam Deflection
Beam deflection is a crucial aspect of structural engineering, as it concerns how beams react under transverse loads. Deflection, the deformation of a beam under load, is significant because it directly affects both structural integrity and serviceability. Engineers must measure deflection to ensure stability and to avoid issues such as excessive sagging.
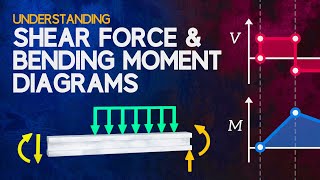
Governing Equation of the Elastic Curve
Based on the Euler-Bernoulli beam theory, the governing equation for beam deflection is given by the second-order differential equation:
$$
\frac{d^2y}{dx^2} = \frac{M(x)}{EI}
$$
where:
- y(x) is the deflection as a function of the beam's position,
- M(x) is the bending moment,
- E is Youngβs modulus, and
- I is the moment of inertia of the beam's cross-section.
Double Integration Method
To compute deflection using the double integration method, engineers perform the following steps:
1. Begin with the bending moment equation,
2. Integrate to find the slope,
3. Integrate again to find deflection,
4. Apply boundary conditions specific to the support conditions of the beam (e.g., simply supported, cantilever).
Common Loading Cases
Specific loading cases have established formulas to calculate maximum deflection:
- Cantilever with point load: $$\delta_{max} = \frac{PL^3}{3EI}$$
- Simply supported beam with central point load: $$\delta_{max} = \frac{PL^3}{48EI}$$
- Simply supported with UDL: $$\delta_{max} = \frac{5wL^4}{384EI}$$
Computation of Slopes and Deflections
The slope, important for design considerations, is calculated as:
$$ΞΈ = \frac{dy}{dx}$$
Moment Area Method
The Moment Area Theorem, or Myosotis Method, helps in analyzing beams subjected to distributed loads. It includes two main theorems relating slope changes and deflection measurements to the area under the M/EI diagram.
This section has introduced fundamental concepts in beam deflection that are essential for structural analysis, particularly for engineers tasked with ensuring safe and functional designs.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Beam Deflection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When subjected to transverse loads, beams undergo bending and deflection.
Detailed Explanation
Beam deflection refers to the bending of beams when they are loaded with forces acting perpendicular to their length. This bending causes the beam to deform from its original straight shape. It is important to understand how and why this happens, as it helps in predicting how a structure will behave under load.
Examples & Analogies
Think of a diving board: when a person steps onto it, the board bends downward in the middle. This bending is the beam deflection. Just like the board needs to be sturdy enough to hold someone without breaking, engineers must ensure that beams in buildings can handle loads without excessive bending.
Importance of Measuring Deflection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Measuring deflection is crucial for:
β Ensuring structural integrity
β Avoiding serviceability issues like excessive sagging.
Detailed Explanation
Measuring how much a beam deflects is crucial for two key reasons. Firstly, it ensures structural integrity, meaning it helps verify that the structure is safe and able to support loads without risk of collapse. Secondly, avoiding serviceability issues like excessive sagging ensures that the structure remains functional and visually appealing. Excessive deflection can lead to cracks or misalignment in other structural components, leading to more serious issues.
Examples & Analogies
Imagine a bridge: if the beams bend too much under the weight of cars, it could not only be dangerous but also cause the bridge to look unstable, making drivers hesitant to cross. Engineers carefully consider deflection to design safe and functional structures, much like how a strong yet flexible trampoline must support jumpers without sagging excessively.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Deflection: The movement of a beam under load.
-
Bending Moment: The internal forces causing bending.
-
Moment of Inertia: Resistance to change in shape.
-
Young's Modulus: Material stiffness characteristic.
-
Double Integration Method: Calculating deflection via integration.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A simply supported beam with a point load at the center travels 2 inches downward under a load of 1000 pounds.
-
A cantilever beam extending 10 feet with a 200-pound load at the free end deflects 5 inches.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When beams bend and sag a lot, Deflection shows us what we've got!
π Fascinating Stories
-
Imagine a bridge made of beams, each one bending under the weight of passing cars. Solving for deflection tells us how much each beam can safely withstand without losing its strength.
π§ Other Memory Gems
-
Remember 'Bβ«D' for Beam Integration Deflection, to recall the steps needed to find deflection using the double integration method.
π― Super Acronyms
Use 'BEND' - Beam Elasticity, Nosing down, Deflection!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Deflection
Definition:
The displacement of a beam from its original position under load.
-
Term: Bending Moment
Definition:
The internal moment that induces bending in a beam.
-
Term: Youngβs Modulus
Definition:
A measure of the stiffness of a solid material.
-
Term: Moment of Inertia
Definition:
A property that measures an object's resistance to bending and rotation.
-
Term: Double Integration Method
Definition:
A technique for calculating deflection by integrating the bending moment equation twice.
-
Term: Moment Area Method
Definition:
A theorem that relates the area under the M/EI diagram to changes in slope and deflection.