Principle of Virtual Work
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Principle of Virtual Work
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're starting with the Principle of Virtual Work. This principle states that for a system in equilibrium, the total virtual work done by internal and external forces is zero. Can anyone tell me what virtual work means?

Is it like the work that we calculate when forces are applied, but it's imaginary?

Exactly! Virtual work is computed during hypothetical infinitesimal displacements under the constraints of a system. Remember, we've got our equation δW = δW_internal + δW_external = 0. Who can explain why this is important?

It helps analyze structures that can't be solved with regular equilibrium equations!

That's correct! Great job!
Applications of the Principle
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's talk applications. Can anyone think of why this principle is utilized in structural mechanics specifically?

It's used when we can't apply straightforward equilibrium equations, right?

Correct! This principle comes in handy for statically indeterminate systems. Now, when we consider structures like beams and trusses, how do we apply this principle conceptually?

We consider virtual displacements for the structures to evaluate the forces.

Exactly! Virtual displacements help assess how the structure reacts to loads without needing direct measurements.
Understanding Equilibrium and Virtual Work
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's link equilibrium to virtual work. What does equilibrium mean in mechanics?

It means the sum of forces and torques acting on a system is zero.

Exactly! And when applied to our principle, why do we get zero total virtual work?

Because the internal forces balance out the external forces in a stable configuration!

Well explained! Remember, understanding these connections deepens our comprehension of structural stability.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In structural mechanics, the Principle of Virtual Work is vital for analyzing statically indeterminate systems. It asserts that the total virtual work done by internal and external forces remains zero under equilibrium conditions, facilitating the study of displacements and stability in complex structures.
Detailed
Principle of Virtual Work
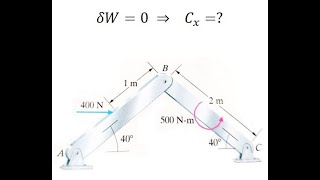
The Principle of Virtual Work is a powerful concept used in mechanics, which states that for any system in equilibrium, the total virtual work done by internal and external forces is zero. This is summarized in the equation:
δW = δW_internal + δW_external = 0
This principle is particularly useful for analyzing statically indeterminate systems and finds significant application in structural mechanics where direct equilibrium equations are challenging to apply.
In essence, this principle helps in formulating problems where the constraints and reactions are intricate, ensuring that structures remain stable under defined loads. Utilizing this principle allows engineers and physicists to bridge complex mechanical systems into solvable forms.
Youtube Videos


![[L23] Beam Theory – 3: Lateral Loading – Bending: Using Principle of Virtual Work](https://img.youtube.com/vi/O3o8ouIZi3M/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Principle of Virtual Work
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Principle of Virtual Work states that for a system in equilibrium, the total virtual work done by internal and external forces is zero for any virtual (imaginary, infinitesimal) displacement consistent with constraints.
Detailed Explanation
The Principle of Virtual Work is an important concept in mechanics that applies to systems in equilibrium. It conveys that if a system is balanced (in equilibrium), any small changes or imaginary shifts that we can imagine (virtual displacements) will not lead to any net work being done when considering both the forces within the system (internal forces) and the forces acting upon it from the outside (external forces). Mathematically, this is expressed as the sum of the virtual work from internal forces plus the virtual work from external forces equaling zero: δW = δW_internal + δW_external = 0.
Examples & Analogies
Imagine a perfectly balanced seesaw with two children of equal weight sitting at either end. If one child were to slide slightly to the side (an imaginary shift), the seesaw would remain balanced (no net work done), as the internal forces (the seesaw's structure sustaining both children) and external forces (gravity acting equally on both) result in no overall change. This simplicity illustrates equilibrium and how the principle applies.
Application of the Principle
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
δW = δW_internal + δW_external = 0
● Useful in analyzing statically indeterminate systems
● Applied in structural mechanics, especially where direct equilibrium equations are difficult to apply.
Detailed Explanation
The principle is particularly beneficial in analyzing statically indeterminate systems, which are structures where the static equilibrium equations alone are insufficient to find the internal forces and support reactions. In these scenarios, the Principle of Virtual Work provides an alternative method to derive the required information. It's widely used in structural mechanics for situations where applying traditional methods might be complex or impractical. For example, when dealing with continuous beams or structures with redundancy, this principle simplifies the analysis.
Examples & Analogies
Consider a complex bridge with multiple supports. Traditional methods may struggle to analyze every internal force due to the bridge's numerous connections and potential points of movement. However, applying the Principle of Virtual Work allows engineers to visualize potential displacements and calculate forces without simplistically reducing the structure, depicting how different parts interact through virtual work.
Key Concepts
-
Equilibrium: The state where the sum of forces and torques is zero.
-
Virtual Displacement: An imaginary change in configuration for calculative purposes in mechanics.
-
Statically Indeterminate Structures: Systems that need additional equations or principles to solve their unknown forces.
Examples & Applications
Analyzing a beam supported at both ends under uniform load using the Principle of Virtual Work to determine deflections.
Using virtual work to evaluate the stability of a truss under varying loads.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a structure so fair, work must be balanced with care; virtual moves, keep the scene, equilibrium's the ultimate dream.
Stories
Imagine a seesaw perfectly balanced with kids on either side. They can wiggle, but as long as they maintain that balance, no one falls off. This is how the Principle of Virtual Work functions—in maintaining balance through virtual adjustments.
Memory Tools
VOW: Virtual Work = Overall Weight, where V stands for Virtual, O for Overall, and W for Weight as a reminder of the balance principle.
Acronyms
BEFORE -> Balance, Equilibrium, Forces, Overall, Resultant, Equilibrium.
Flash Cards
Glossary
- Virtual Work
The work calculated for an imaginary or infinitesimal displacement of a system, used in mechanical analysis.
- Equilibrium
A state where the sum of the forces and torques acting on a system is zero, ensuring no motion occurs.
- Statically Indeterminate Systems
Structures that cannot be solved by static equilibrium equations alone due to excess unknown forces.
Reference links
Supplementary resources to enhance your learning experience.
