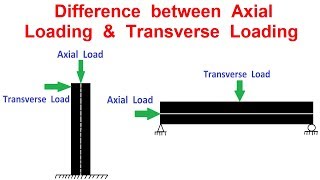
Introduction to Transverse Loading on Beams
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Types of Loads
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's start by discussing the various types of loads that can act on a beam. Does anyone know what a point load is?

Is it a force concentrated at one single location?

Exactly! It's concentrated at one point. Now, what about a uniformly distributed load?

That would be spread evenly along the length of the beam, right?

Correct! Lastly, how about a uniformly varying load?

That changes in intensity along the length!

Great job! To remember these, you can think of them as 'Point'—'Single', 'Uniform'—'Even', and 'Varying'—'Changing'.
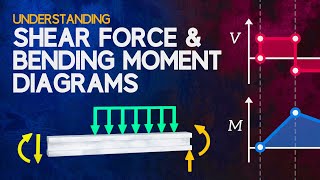
Shear Force and Bending Moment Diagrams
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's delve into shear force and bending moment. What do you think shear force refers to?

Isn't it an internal force acting perpendicular to the beam?

Exactly! And what about bending moment?

It’s the internal moment that causes bending in the beam, right?

Correct! Now, can anyone tell me the significance of the slope of the bending moment diagram?

It represents the shear force!

Great! Let’s remember it this way: 'Bending Moments Bend, Shear Forces Slide.'
Types of Beam Supports
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Can someone recap the types of beam supports we discussed?

There are simply supported beams, cantilevers, overhanging beams, fixed beams, and guided beams.

Well done! How does a cantilever beam differ from other types?

It's fixed at one end and free at the other.

Precisely! This distinction is crucial in understanding how loads are transferred and supported. Remember: 'C for Cantilever - Only One Fixed End.'
Static Determinacy
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

What do we mean by statically determinate beams?

They have an equal number of reactions and equilibrium equations!

That's right! And what about statically indeterminate beams?

They have more unknowns than equations, hence require additional analysis.

Absolutely! Remember: 'Determinate – Equal, Indeterminate – More!'
Theory of Bending
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Can someone summarize the assumptions of the theory of bending?

The material is homogeneous and isotropic, and plane sections remain plane after bending.

Correct! And what is the significance of the bending moment equation?

It relates moment, stress, and curvature, helping to establish the beam's behavior under loads.

Exactly! Let’s remember: 'Bending Moment equals Stress and Curvature'.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section covers the fundamental concepts of transverse loading on beams, including various load types, shear force and bending moment diagrams, types of beam supports, and the basic theory of bending. It highlights the importance of understanding these elements to analyze structural integrity in civil engineering.
Detailed
Introduction to Transverse Loading on Beams
This section is designed to introduce students to the mechanics involved in analyzing beams subjected to transverse loads. Beams serve as crucial structural elements designed to resist bending and shear forces that act perpendicular to their longitudinal axis.
Types of Loads
Three primary types of loads are defined:
- Point Loads: These are concentrated at a single location on the beam and can create localized stress.
- Uniformly Distributed Loads (UDL): These are loads that are spread evenly across a certain length of the beam, leading to a consistent distribution of stress.
- Uniformly Varying Loads (UVL): These loads exhibit a linear or non-linear intensity that varies along the length of the beam.
Shear Force and Bending Moment Diagrams
The section emphasizes the concepts of shear force (internal force acting perpendicular to the beam) and bending moment (internal moment causing bending), highlighting the relationship between the slope of bending moment diagrams and shear forces, as well as the significance of points of contraflexure.
Types of Beam Supports
Different types of supports (Simply Supported, Cantilever, Overhanging, Fixed Beam, and Guided Beams) affect how beams behave under loads, which is vital for determining the reactions and the internal forces during analysis.
Static Determinacy and Indeterminacy
The distinction between determinate and indeterminate beams is presented, outlining how the number of reactions in a statically determinate beam matches the equilibrium equations available, while statically indeterminate beams require additional methods for analysis.
Theory of Bending
The assumptions underpinning beam bending mechanics are explained, including the materials’ homogeneous and isotropic nature and plane sections remaining plane post-bending. The bending equation is additionally provided, which relates moment, stress, and radius of curvature.
Neutral Plane and Shear Stress Distribution
The concepts of pure bending, the neutral plane, and shear stress distribution across the beam depth are discussed to further elucidate the internal mechanics at play. Understanding these factors is critical for predicting structural performance under various loading conditions.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Beams and Transverse Loading
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Beams are structural elements designed to resist bending and shear when subjected to transverse loads (forces perpendicular to their axis).
Detailed Explanation
Beams are vital components in construction and engineering. When a beam is placed between two supports and a force is applied perpendicular to its length, this is known as a transverse load. The beam's primary role is to resist bending (which tries to curve it) and shear (which tends to slide sections of the beam past one another). Understanding how beams react to these forces is essential for ensuring structural integrity.
Examples & Analogies
Imagine a diving board supported at both ends. When a diver jumps on it, their weight creates transverse loads. The board bends downwards in the center, demonstrating bending, while the strength of the board prevents it from snapping, showing its ability to resist shear.
Types of Loads
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Types of Loads:
● Point Load: Concentrated at a single location
● Uniformly Distributed Load (UDL): Spread evenly over a length
● Uniformly Varying Load (UVL): Intensity varies linearly or nonlinearly along the length
Detailed Explanation
Different types of loads affect how a beam behaves. A point load is a force applied at one specific location, like a weight dropped from above. A uniformly distributed load (UDL) spreads weight evenly across the beam, like a person standing along a bench. A uniformly varying load (UVL) changes in intensity, which could mimic the wind pressure fluctuating across a bridge. Recognizing these types helps engineers design beams that handle loads effectively.
Examples & Analogies
Think of a trampoline. If one person stands still in the middle (point load), the trampoline will dip significantly at that point. But if everyone spreads out evenly on the trampoline (UDL), it will take a gentle curve instead. If one end is heavier than the other (UVL), the trampoline will tilt, showing how the load affects the beam differently.
Key Concepts
-
Types of Loads: Point Loads, Uniformly Distributed Loads, and Uniformly Varying Loads are critical in analyzing beams under load.
-
Shear Force and Bending Moment: Understanding these internal forces is essential for structural analysis.
-
Static Determinacy vs. Indeterminacy: Determines how we analyze beams and their reactions under loads.
-
Theory of Bending: Incorporates assumptions about material properties and the behavior of beams under load.
Examples & Applications
A beam subjected to a point load at its midpoint can be analyzed for maximum bending moment and shear force.
A beam uniformly supported with a distributed load can illustrate how load affects the deflection and shear forces through various sections.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Loads can point, spread, or change with might, beams bear them well, they're built just right!
Stories
Imagine a superhero beam that can withstand any force, whether it's a single punch, a gentle breeze, or a mighty storm – illustrating how different loads affect its strength.
Memory Tools
Remember for loads: P for Point, U for Uniform, V for Varying!
Acronyms
LBS
Loads
Beams
Shear Forces!
Flash Cards
Glossary
- Beam
A structural element that resists bending and shear under transverse loads.
- Point Load
A concentrated load applied at a single location on the beam.
- Uniformly Distributed Load (UDL)
A load that is evenly spread across the length of a beam.
- Shear Force (SF)
An internal force that acts perpendicular to the longitudinal axis of the beam.
- Bending Moment (BM)
An internal moment that arises in the beam due to applied loads causing bending.
- Contraflexure
A point on the beam where bending moment changes sign, indicating zero bending moment.
- Static Determinacy
A condition where the number of reactions equals the number of equilibrium equations.
- Moment of Inertia (I)
A measure of an object's resistance to bending, linked to its cross-sectional shape.
- Neutral Plane
The plane within a beam's cross-section where no bending stress occurs.
Reference links
Supplementary resources to enhance your learning experience.
