Non-uniform Bending
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Non-uniform Bending
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are diving into non-uniform bending. Can anyone tell me how it differs from pure bending?

I think pure bending has a constant moment along the beam.

Exactly! In pure bending, the bending moment is constant. Non-uniform bending, however, involves varying bending moments. What do you think this means for the shear forces in the beam?

I imagine it means there's a net shear force acting on the cross-section, right?

Correct! Whenever there’s a variation in the moment, there's a non-zero shear force. Let's remember this with the acronym 'V-M', which stands for Shear Force Variation due to Moment Variation.

Got it! V-M indicates that if the bending moment varies, so does the shear force.

Great summary! Let's quickly review: in pure bending, shear is zero, but in non-uniform, it is non-zero due to varying moments.
Stress Distribution in Non-uniform Bending
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's delve into how non-uniform bending affects the distribution of stress in the beam. Can anyone recall the formula for bending stress?

Is it related to the bending moment, like σ = My/I?

Exactly, that's the formula! In non-uniform bending, we adapt it to account for local bending moments. What's the shape of the stress distribution in this case?

I think it might still be linear, like in pure bending?

Spot on! The distribution remains linear but varies based on local moments. Now let's switch gears and discuss shear stress. How does it compare?

I remember shear stress is affected by shear forces and not the moment directly.

Very well stated! Shear stress is indeed proportional to shear force, impacting how loads are carried through the beam.

So σ is tied to M, while τ is tied to V?

Correct! That's an essential distinction to make. Remember: σ for bending, τ for shear.
Shear Stress in Various Cross-sections
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s explore how different cross-sectional shapes affect shear stress distribution. Who can name a shape we’ve discussed?

How about a rectangular cross-section?

Great choice! For rectangular cross-sections, what do we observe about shear stress at different heights?

Shear stress is highest at the centroid and zero at the top and bottom surfaces.

Correct again! Now let’s discuss circular cross-sections. Does it operate under the same principles?

I think it’s different because shear stress can’t be assumed independent of the z-axis, right?

Exactly! It introduces nonlinear distributions, so keep that in mind during analysis. We can summarize: each cross-section behaves differently under shear, affecting stress distribution.
Analysis of I-beams
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To wrap up, let's examine I-beams. Can someone describe their unique feature affecting shear stress?

I think the width varies significantly, impacting the shear stress patterns.

Absolutely! The abrupt changes in width lead to jumps in shear stress. Now, if we plotted shear stress across an I-beam, what might it look like?

Maybe a graph with peaks corresponding to the flanges of the beam?

Exactly! Understanding these variations is key for structural design. Remember the concept: wider sections lead to different shear distributions.

This makes it clear why engineers need to consider cross-section shapes in design!

Precisely! Design effectiveness hinges on these principles. Keep engaged with these discussions as we move forward!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the concept of non-uniform bending in beams, contrasting it with pure bending. We derive important relationships between shear forces and bending moments, and examine how these affect stress distributions within the beam's cross-section.
Detailed
Non-uniform Bending
In the study of beam mechanics, bending of beams can be categorized into pure (or uniform) bending and non-uniform bending. Pure bending occurs when the bending moment remains constant along the beam's length, while in non-uniform bending, the bending moment changes.
Key Points:
- Definition and Introduction: Non-uniform bending refers to scenarios where the bending moment varies, resulting in non-constant curvature of the beam.
- Basic Relationships: We revisit the relationship between bending moment (M), modulus of elasticity (E), and curvature (κ), expressed as:
$$ M = EIκ $$
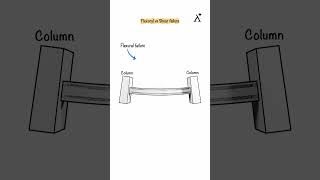
As this moment is not constant along the beam’s length, the shear force (V) must act on the beam's cross-section. - Shear Force and Moment Balance: By cutting a small portion of the beam and performing a moment balance, we discover that a variation in moment necessitates a non-zero shear force acting on the cross-section, which fundamentally differs from pure bending where shear force is zero.
- Stress Distributions: The variations of both bending stress (σ) and shear stress (τ) within the beam's cross-section are explored, using local bending moments for analysis.
- Stress Analysis for Different Cross-sections: We analyze the shear stress in various cross-sectional dimensions, including rectangular, circular, and I-beams, noting how width and shape impact the distributions of stress.
- Comparative Stress Analysis: The derived relationships showcase that while bending stress is proportional to bending moment, shear stress is tied to shear force acting on the beam.
Through these examinations, students gain a deeper understanding of how varying loading conditions affect beam mechanics, necessitating careful consideration in design and analysis.
Youtube Videos

![Mechanics of Solids [Intro Video]](https://img.youtube.com/vi/TdmQGMUbUVw/mqdefault.jpg)







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Non-uniform Bending
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In case of pure bending, we had the same moment acting on every cross-section. For this reason, pure bending is also called uniform bending. We will now move on to non-uniform bending of a beam where bending moment is not uniform along the length of the beam. In the previous lecture, we had derived the following relation for bending moment M and curvature κ:
M = EIκ. (1)
If bending moment M is not constant along the length, bending curvature will also not be constant. We now consider another case of loading where we can also have a distributed load b(x) acting on the beam.
Detailed Explanation
In this section, we introduce the concept of non-uniform bending, which occurs when the bending moment varies along the length of the beam. Unlike pure bending, where the moment is constant (leading to a uniform curvature), non-uniform bending leads to changes in curvature at different points along the beam. The relationship M = EIκ relates the bending moment (M) to the curvature (κ) of the beam, with E being the modulus of elasticity and I the moment of inertia. This equation shows that if the bending moment changes, so does the curvature, indicating that the beam will bend differently at various sections due to the varying loads.
Examples & Analogies
Imagine a flexible rubber band. If you pull it uniformly from both ends, it stretches evenly (pure bending). Now, if you pull it harder at one end, the band bends more in that area, leading to a non-uniform stretch (non-uniform bending).
Static Equilibrium and Shear Force
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The load b(x) is assumed to act in +y direction. Let us cut a small part of the beam of length ∆x at a distance x from the clamped end. On this section, apart from the distributed load, there will be bending moment as well as shear force acting at the two ends. By convention, for the cross-section having normal in +x direction, shear force acting in +y direction is considered as positive. We denote this shear force by V. The net moment on this part of the beam must be zero about any point.
Detailed Explanation
In analyzing non-uniform bending, we consider a small segment of the beam of length ∆x. This segment experiences both a distributed load (b(x)) acting downward and a shear force (V) that acts on the cross-section. We define forces acting in specific directions as positive or negative for consistency. For the system to be in static equilibrium, the sum of the moments about any point, such as one end of the beam segment, must equal zero. This principle helps derive relationships between bending moments and shear forces.
Examples & Analogies
Think of holding a ruler horizontally while applying weight in the middle. The ends of the ruler push upward with force (shear), and how much it bends depends on where the weight is applied. Each section of the ruler reacts to this force, and the total bending must balance out.
Relation Between Bending Moment and Shear Force
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We have derived an important relation between the variation of bending moment and shear force. It says that whenever moment varies along the beam, there has to be a non-zero shear force acting on the beam’s cross-section. The case of zero shear force corresponds to the case of pure bending where moment is constant throughout the length of the beam.
Detailed Explanation
This chunk emphasizes a critical relationship in beam mechanics: when the bending moment changes along the length of a beam, this indicates the presence of shear force in the cross-section. If the shear force were zero, it would mean that the bending moment is uniform, corresponding to pure bending conditions. Understanding this relationship is essential for analyzing beams under various load conditions.
Examples & Analogies
Consider a tree branch bending under the weight of snow. If the snow load is heavier at one end, the branch must experience internal forces (shear) to counterbalance that weight. If no snow is present, the branch would remain straight without bending—similar to pure bending in beams.
Variation of Stress in Non-uniform Bending
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For the case of non-uniform bending, the variation of σ can be taken to be the same as in the last lecture. We just have to use local bending moment in the formula:
σ = M(y) / I, (5)
In the above expression, y represents the distance from the neutral axis as earlier.
Detailed Explanation
When discussing stresses (C3) resulting from non-uniform bending, we apply the same formula used for uniform bending, but we must substitute the local bending moment into the equation. Here, σ is the stress acting on the beam at a distance y from the neutral axis, while I is the moment of inertia. This shows that stress distribution within the beam is affected by the bending moment at that particular section, ensuring that students understand how bending influences stress.
Examples & Analogies
Think of a piece of chewing gum stretched between your fingers. The side of the gum closer to your hand experiences more tension (stress) the further you pull it. In bending beams, similarly, areas further from the neutral axis endure more stress.
Key Concepts
-
Non-uniform Bending: Bending where the moment varies along the beam length.
-
Moment-Balance: Variation in bending moment requires corresponding shear force.
-
Stress Distribution: Varies based on location and type of beam cross-section.
-
Shear Stress: Proportional to the shear force acting on the cross-section.
Examples & Applications
In a simply supported beam subjected to a varying load, the resultant bending moment diagram will illustrate how moments change, leading to different shear forces.
For a rectangular beam, shear stress can be calculated at various points along its height using the formula τ = VQ/Ib.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
For beams that bend and shear, remember V and M are near!
Stories
Imagine a beam in distress, bending under a load's press. Its moments shift, so forces shift too, V leads the dance, while M follows through.
Memory Tools
Remember: 'B&M' - for Bending and Moment relationships!
Acronyms
V-M stands for Shear Force Variation due to Moment Variation.
Flash Cards
Glossary
- Bending Moment (M)
The moment that induces bending of the beam, different values result in varying curvatures.
- Shear Force (V)
The force that acts perpendicular to the beam's length causing shear stress.
- Bending Stress (σ)
The stress experienced by the beam material due to bending moment.
- Shear Stress (τ)
The stress that arises from shear forces acting on the beam's cross-section.
- Crosssection
A cut through the beam to analyze internal forces and stress patterns.
Reference links
Supplementary resources to enhance your learning experience.
