Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Timoshenko Beam Theory
Unlock Audio Lesson
Welcome class! Today we're discussing the Timoshenko Beam Theory. Can anyone tell me how this theory differs from the Euler-Bernoulli beam theory?
The Euler-Bernoulli theory assumes that the centerline tangent and cross-section normal are aligned, right?
Exactly! In Timoshenko's theory, we assume they are not aligned. This means we have two variables: the deflection and the cross-section rotation. Can anyone recall why this distinction is important?
It’s important for understanding shear deformation in shorter beams.
Correct! This brings significant accuracy, especially in beams with lower aspect ratios. Remember: more variables can lead to more precise modeling.
Governing Equations of TBT
Unlock Audio Lesson
Now, let's delve into the governing equations of TBT. Can anyone write down the expression for shear force in relation to deflection and rotation?
Is it dy/dX - θ = V/(kGA)?
Good job! And what about the moment-curvature relationship?
That would be EIκ = M.
Exactly! Remember that these equations help us understand the interactions between shear forces and moments in a beam. It's a system of equations, and solving these gives us insight into beam behavior.
Real-Life Application of TBT
Unlock Audio Lesson
Let’s apply TBT to a cantilever beam subjected to a transverse load. What would our first step be?
Finding the shear force and bending moment distribution?
Exactly! By sketching a free body diagram, how would we conclude the moment at the point we cut?
We’d use the equation M(X) = P(L−X) for the moment balance.
Right on point! This interpretation allows us to find the deformations accurately with TBT, giving us a clearer picture than EBT.
Choosing Between EBT and TBT
Unlock Audio Lesson
Now, how do we decide when to use Timoshenko beam theory versus Euler-Bernoulli beam theory?
If the results from TBT are similar to those from EBT, we just apply EBT, right?
Exactly! EBT is simpler and valid when shear can be neglected. What factor helps us determine this?
The aspect ratio of the beam?
Spot on! When the aspect ratio is greater than around 10, we can safely use EBT. Always consider the geometry and material properties!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Timoshenko Beam Theory distinguishes itself by accepting that the cross-sectional normal does not necessarily align with the centerline tangent during deformation, thus accounting for both deflection and cross-section rotation as independent variables. The theory derives governing equations that relate shear force, bending moment, and curvature for more accurate predictions compared to Euler-Bernoulli beam theory, particularly in beams of lower aspect ratios.
Detailed
Detailed Summary of Timoshenko Beam Theory
Timoshenko Beam Theory (TBT) provides a refined approach to beam analysis by incorporating both shear deformations and rotations of beam cross-sections, which is particularly significant in short beams where shear deformation is pronounced. Unlike the Euler-Bernoulli beam theory, where it is assumed that the centerline tangent aligns with the cross-section normal, TBT allows for a disconnect between these elements. This results in two independent kinematic variables: the deflection of the beam and the rotation of the cross-section.
Governing Equations
Within TBT, the governing equations emerge from the consideration of an initially straight beam undergoing arbitrary loads, leading to new relationships between shear forces and bending moments, emphasizing the importance of shear strain at the centroid.
The equations are expressed as follows:
- Shear Force Relationship:
$$\frac{dy}{dX} - \theta = \frac{V}{kGA}$$ - Moment-Curvature Relation:
$$EI \kappa = M$$
These equations form a coupled first-order linear differential system, requiring boundary conditions for completion.
Example and Application
An example explored is a cantilever beam subjected to a transverse load, comparing results obtained through TBT with those from Euler-Bernoulli theory to illustrate the improved accuracy of TBT in specific scenarios. This section also discusses criteria for choosing between the two theories based on aspect ratios and material properties.
Key Insights
The theoretical groundwork provided by TBT becomes crucial in engineering applications, especially as beam dimensions decrease or when materials reveal significant shear effects. This detailed understanding allows engineers to predict and mitigate potential failures more effectively through appropriate design choices.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Timoshenko Beam Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
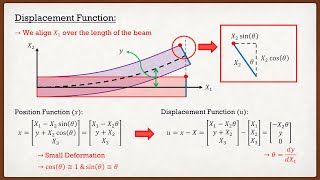
In Euler-Bernoulli beam theory, it is assumed that the centerline tangent and the cross-section normal are aligned as shown in Figure 1a. So, we have only one kinematic variable which is the deflection of the beam y: we can obtain the cross-section orientation from its derivative, i.e., . However, in Timoshenko Beam Theory (TBT), we do not assume the centerline tangent and cross-section normal to be aligned as shown in Figure 1b. Thus, this is a more general theory than EBT: we now have deflection y and cross-section rotation θ as two independent unknowns.
Detailed Explanation
The Timoshenko Beam Theory expands upon the classical Euler-Bernoulli beam theory by addressing some of its limitations. In Euler-Bernoulli theory, the assumption is made that the angle between the beam's central axis and the cross-section remains constant during bending, which simplifies the analysis. This means that only one variable, the deflection of the beam (y), is needed to determine the deformation. In contrast, Timoshenko theory recognizes that the cross-section can rotate independently of the central axis, resulting in two variables: deflection (y) and rotation (θ). This acknowledgment leads to a more accurate representation of short beams where shear deformations become significant.
Examples & Analogies
Imagine a fishing rod when you cast a line. The rod bends as you apply force, but the top part of the rod (the tip) may twist slightly due to the force of the line pulling on it. The traditional theory would not account for that twist, while Timoshenko's theory would, allowing for a better understanding of how the rod behaves under load.
Governing Equations of Timoshenko Beam Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
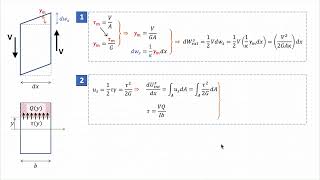
Let us consider a beam which is initially straight and gets deformed due to some arbitrary loading. The centerline tangent makes an angle α with the horizontal which implies (assuming the slope to be small enough). The deformed cross-section normal makes an angle θ with the horizontal. Thus, the angle between the cross-sectional line (shown as solid green line in Figure 2b: it should not be confused with cross-section normal) and the centerline tangent becomes . In the undeformed straight beam, the angle between the cross-sectional line and the centerline tangent was which, upon deformation, changes to . As shear strain measures the changes in angle (initial-final angle) between perpendicular line elements, we have.
Detailed Explanation
When a beam is subjected to loading, it bends and rotates, changing the orientation of both its centerline and cross-sections. In Timoshenko Beam Theory, we analyze these changes by measuring the angles formed between the original and deformed shapes of the beam. The angle between the centerline's tangent and the cross-sectional line is critical because it helps in determining shear strains that develop as the beam bends. The theory allows for a relationship between shear force and cross-sectional shear strain, leading to equations that can be used to analyze the beam's loading effectively.
Examples & Analogies
Think about a slinky toy. When you pull on one end, the coils not only get stretched (deflection) but also twist together (rotation). Just like in beams, the changes in position and angles of the coils can be studied to understand how they behave under force, similar to how Timoshenko Beam Theory analyzes bending and rotation in beams.
Examples and Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
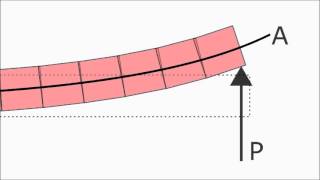
Consider the problem that we had solved using EBT in the previous lecture. A transverse force P is applied at the free end of a beam which is clamped at the other one end. This problem is also called a Cantilever Problem. We would like to solve for the deformation using TBT and compare the result with those of EBT.
Detailed Explanation
In practical applications, like a cantilever beam, we can use Timoshenko Beam Theory to analyze how the beam responds to forces. By applying a load at the free end of the cantilever while it is fixed at the other end, we can calculate the resulting displacement and compare these values obtained from TBT with those from the simpler Euler-Bernoulli theory. This comparison helps in realizing the effects of shear deformation, which are significant in short and deep beams where EBT’s conservative assumptions would yield inaccurate results.
Examples & Analogies
Picture a diving board held at one end. When a diver steps on the far end, the board bends, not just downward (deflection) but also slightly twists. Using Timoshenko theory helps in accurately predicting the board's behavior under this load as it combines both bending and twisting effects, unlike the simpler approach that might miss important details.
When to Use Timoshenko vs. Euler-Bernoulli Theory
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us now explore which of the two theories to use in a given scenario. If the result from TBT is very close to the one from EBT, then we can simply apply EBT and neglect the effect of shear.
Detailed Explanation
Choosing the correct beam theory is essential for accurate analysis. When the analysis yields similar results between TBT and EBT, it's acceptable to use the simpler Euler-Bernoulli theory since it reduces the complexity of calculations. However, in applications where shear deformation is significant, as with short or thick beams, Timoshenko theory should be used for a more accurate representation of the actual behavior, ensuring safety and reliability in design.
Examples & Analogies
Consider a narrow wooden plank versus a thick steel beam. For the thin plank, a simpler approach might work well. But if it were a thick steel beam subjected to heavy loads, neglecting shear effects could lead to unsafe designs. Using Timoshenko theory provides a more accurate understanding of how much the beam would bend and twist under stress, much like using a specialized tool for a specific job.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Shear Deformation: The change in the angle of cross-sections of a beam due to shear forces.
-
Cross-section Rotation: The change in orientation of the cross-section of a beam in response to bending.
-
Governing Equations: The equations relating shear force and bending moment that determine beam behavior.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A practical application of TBT involves analyzing a cantilever beam with a transverse load to show how predictions differ from EBT.
-
Another example is calculating the shear stress distribution in a rectangular beam cross-section.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When beam is short, Timoshenko’s the court; shear and rotation, its pure dedication.
📖 Fascinating Stories
-
Imagine a beam struggling to stay straight. Timoshenko came and said, 'Don't fret, let's account for what’s rotating and shearing as well.'
🧠 Other Memory Gems
-
Remember TBT as 'Two Variables,' representing deflection and rotation.
🎯 Super Acronyms
Use 'TRAC' for Timoshenko
- T: - Torsion
- R: - Rotation
- A: - Area
- C: - Cross-section.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Timoshenko Beam Theory
Definition:
A theory that incorporates shear deformation and cross-section rotation in beam analysis, offering a more accurate representation of beam behavior, especially in short beams.
-
Term: EulerBernoulli Beam Theory
Definition:
A classical beam theory that assumes straight beams with aligned centerline tangents and cross-section normals, neglecting shear deformations.
-
Term: Shear Force
Definition:
A force that acts parallel to the beam cross-section, resulting in deformation.
-
Term: Bending Moment
Definition:
The moment that induces bending of the beam due to applied loads, leading to curvature in the beam.
-
Term: Aspect Ratio
Definition:
The ratio of the length of the beam to its width, significant in determining which beam theory to apply.