Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Equilibrium
Unlock Audio Lesson
Today, we're discussing the concept of equilibrium. Can anyone tell me what equilibrium means in a structural context?
I think it means that all the forces acting on the structure balance out.
Exactly! In equilibrium, the sum of all forces acting on a body is zero. This is expressed as \( \sum F = 0 \). Let's break this down further. Why do we need to know about forces?
To ensure that the structure doesn't collapse or move unexpectedly!
That's right! Understanding forces helps us determine the reactions at the supports. Remember, these reactions are crucial for analyzing the stability of the structure.
What types of support are there?
Great question! There are three primary types of support: roller supports, hinge supports, and fixed supports—can anyone explain what each one does?
A roller can rotate but not move in one direction; a hinge allows rotation but doesn't allow displacement.
Perfect! And fixed supports prevent rotation and displacements in all directions. Let's recap: equilibrium focuses on balancing forces and moments to maintain stability.
Equations of Equilibrium
Unlock Audio Lesson
Now, let's discuss the equations of equilibrium. How many equations do we use for different structures?
I've seen equations like \( \sum F_x = 0 \), \( \sum F_y = 0 \), and \( \sum M = 0 \).
Exactly! In a 2D structure, we use two force equations and one moment equation. But what if we have a 3D structure?
Then we need three force equations and three moment equations!
Right again! That means for every dimension we add, we adjust the number of equations accordingly. Why is this important?
It’s important because it ensures that we consider all directions of force.
Absolutely! Each equation must balance out to zero, reflecting that the system is in static equilibrium.
Static Determinacy
Unlock Audio Lesson
Let’s explore the concept of static determinacy. What does it mean for a structure to be statically determinate?
It means you can find all reactions using just the equilibrium equations without needing anything else.
Correct! But what happens when a structure is statically indeterminate?
Then we need extra equations to solve for the reactions, like displacement compatibility.
Great recall! Knowing whether a structure is determinate helps us choose the right analysis method. Can anyone give an example of a statically indeterminate structure?
Like a rigid plate supported by multiple cables?
Exactly! Remember, understanding whether a structure is determinate or indeterminate is crucial for correct analysis.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the concept of equilibrium in static structures, highlighting how to determine reactions using equations, the importance of support conditions, and the classification of structures into statically determinate and indeterminate categories.
Detailed
Equilibrium in Static Structures
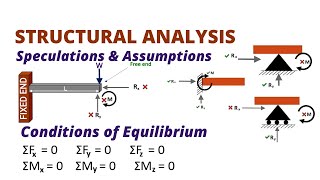
Equilibrium is a critical concept in engineering that refers to the state where the sum of forces and moments acting on a structure is zero. It is essential for ensuring structural stability. The primary equations governing equilibrium are based on Newton's first law of motion, which states that the net force acting on a body at rest must equal zero:
- Summation of Forces:
\[
\sum F = 0
\]
- Summation of Moments:
\[
\sum M = 0
\]
These equations help in determining the reactions at different supports, which can include roller supports (allowing rotation in one plane), hinge supports (allowing rotation without displacement), and fixed supports (preventing both rotation and displacement).
In addition to reactions, the external forces acting on a structure are balanced by internal forces, which contribute to shear and moment diagrams. If additional internal conditions exist, such as hinges, extra equilibrium equations arise, helping to calculate unknown forces. Understanding whether a structure is statically determinate or indeterminate is crucial; statically determinate structures allow reactions to be calculated solely from equilibrium equations, while statically indeterminate structures require additional compatibility conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Equations of Static Equilibrium
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Reactions are determined from the appropriate equations of static equilibrium.
Summation of forces and moments, in a static system must be equal to zero.
Detailed Explanation
In static analysis, the fundamental principle is that for a structure to be in equilibrium, the total sum of forces and the total sum of moments acting on it must be zero. This means that all the forces pulling in one direction must be balanced by forces pulling in the opposite direction, and similarly for moments (which can be thought of as the turning effect caused by forces). Thus, if we have a structure and we know the forces, we can set up equations that sum these forces and moments to ensure balance.
Examples & Analogies
Imagine you are holding a long plank horizontally with one person on each end pushing down with the same force. If both people push down with exactly the same strength, the plank stays level and does not rotate or tilt; this is a simple example of equilibrium with forces and moments being balanced.
Types of Structures and Their Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Structure Type Equations
Beam, no axial forces: ΣF_x = ΣF_y = ΣM_z
2D Truss, Frame, Beam: ΣF_x = ΣF_y = ΣM_z
Grid: ΣF_x = ΣM_y = ΣM_z
3D Truss, Frame: ΣF_x = ΣF_y = ΣF_z = ΣM_x = ΣM_y = ΣM_z.
Detailed Explanation
Different types of structures follow different equations in static equilibrium. For example, a simple beam that is not subject to axial forces requires a sum of forces in both the horizontal (x-direction) and vertical (y-direction), as well as the sum of moments about a point, to be equal to zero. A 2D truss structure includes the same conditions but can have more connections. The equations provide a systematic way to calculate reactions and internal forces at various supports and joints within the structures.
Examples & Analogies
Consider a bridge structure. The bridge acts as a beam that spans across a gap with weights (cars) on it. Engineers need to ensure that the upward reactions from the supporting piers balance out the downward forces (weights of cars), and they calculate this based on the type of bridge—which represents the types of structures mentioned.
Understanding Reactions in Equilibrium
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The right-hand side of the equation should be zero. If your reaction is negative, then it will be in a direction opposite from the one assumed.
Detailed Explanation
When computing reactions using the equations of equilibrium, the expected result typically ends up equating to zero on the right-hand side of the equation. This means that whatever forces or moments you posit must cancel each other out. If the calculated reaction force comes out as negative, it indicates that the actual direction of that force is opposite to the direction you initially assumed it to be. Understanding this can help avoid mistakes in analysis.
Examples & Analogies
Think about a seesaw with a kid on one end and an adult on the other. If you predict both will balance out at an angle, but you assume the smaller child's weight will act downward while the adult's weight acts upward, you may find that your calculations yield a negative number for the child’s side's reaction. This signifies that perhaps the child actually needs to push up instead, which changes your understanding of the physical situation!
External and Internal Forces Interaction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Summation of external forces is equal and opposite to the internal ones. Thus the net force/moment is equal to zero.
Detailed Explanation
In equilibrium analysis, not only do we consider external forces acting on a structure, but we also recognize that these external forces lead to internal forces that must be balanced. This interplay means that if all external influences sum to zero, the internal reactions will also need to sum to zero in order to satisfy the conditions of equilibrium. This relationship is fundamental in understanding how forces distribute within structures.
Examples & Analogies
If you think about a zip line, the cable experiences tension from both the rider (external force) and itself (internal reaction). The external force pulling the system down has to be countered by the tension within the cable, balancing the entire system and keeping the rider safe—this is how the external and internal forces work in harmony!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Equilibrium: The condition where the sum of forces and moments equals zero, ensuring stability in structures.
-
Equations of Equilibrium: Mathematical expressions used to compute forces and moments in static analysis.
-
Types of Supports: Roller, hinge, and fixed supports influence the way forces are distributed in a structure.
-
Static Determinacy: Refers to structures for which reactions can be determined exclusively from equilibrium equations.
-
Static Indeterminacy: Structures requiring more equations than provided by equilibrium alone to find reactions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A beam supported at both ends is analyzed for equilibrium by ensuring that the sum of vertical forces is zero.
-
A truss with multiple connections uses hinges to allow for additional equations that assist in calculating unknown forces.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
A beam must not sway, it must stay, forces at bay lead to a safe day!
📖 Fascinating Stories
-
Imagine a bridge held up by three types of supports. Each support plays a unique role: the roller swings, the hinge turns, and the fixed anchor holds still, together they keep the bridge stable.
🧠 Other Memory Gems
-
To recall support types, think R-H-F: Roller spins, Hinge pivots, Fixed stands still.
🎯 Super Acronyms
For equilibrium, remember S-M-0
- Sum of Forces
- Moments must equal Zero.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Equilibrium
Definition:
The state in which the sum of all forces and moments acting on a structure is zero.
-
Term: Static Determinacy
Definition:
A property of structures where all reactions can be determined using only the equations of static equilibrium.
-
Term: Static Indeterminacy
Definition:
When the reactions of a structure cannot be determined solely from the equations of equilibrium, requiring additional conditions.
-
Term: Reaction Forces
Definition:
Forces at the supports of a structure that counteract external loads.
-
Term: Support Conditions
Definition:
The constraints provided by supports, affecting how loads and forces are transmitted through a structure.