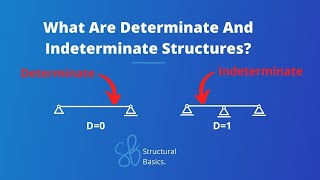
Static Determinacy
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Static Determinacy
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will delve into static determinacy. Can anyone tell me what this term means in the context of structures?

Is it about whether we can calculate the forces in a structure using just equilibrium equations?

Exactly! When a structure is statically determinate, we can determine all reactions based purely on its geometry, boundary conditions, and loads.

And what if we can't determine the reactions using these methods?

Great question! If we can’t, then the structure is statically indeterminate. This is where we need more equations, often related to the compatibility of displacements.

So, in a way, statically indeterminate structures are more complex?

Yes, they require additional analysis, often involving deformation or compatibility conditions. Remember: *More_knowns_than_equations* – is a mnemonic for statically indeterminate!

To summarize, acting under static determinacy allows us to utilize the structure's geometry and loads to find reactions simply.
Understanding Indeterminate Structures
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's look at our example of a rigid plate supported by cables. Can anyone explain what makes this scenario statically indeterminate?

Because there are more unknown forces than there are equilibrium equations?

Correct! Since we have three unknowns but only two equilibrium equations from static equilibrium, we need to introduce an additional equation, usually from the compatibility of displacements.

How do we typically derive that extra equation?

Good inquiry! We often use the fact that in a deformation scenario, the movements of all cables must be compatible. This means they must adjust in such a way that their lengths change consistently.

Ah, so if we calculate the changes in length, we can solve for the unknown forces?

Exactly! At this point, we integrate structural mechanics principles with deformation methods. Always remember to ensure compatibility when dealing with indeterminate structures.

To recap, statically indeterminate structures require additional analysis through compatibility conditions because they have more unknown forces than equations.
Calculation of Forces in Statically Indeterminate Systems
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s solve the problem involving the rigid plate supported by two aluminum cables and a steel cable. Can someone summarize the issue we face here?

We have three unknowns, right? So we cannot solve it using just the two static equilibrium equations.

Precisely! Here, we need the third equation from our displacement compatibility, which states that all displacements must be equal.

So we need to express those displacements in terms of our unknown forces?

Exactly! By establishing a relationship between the forces and the deformation through *P/A = E* and using Young's modulus, we create an equation for displacement based on force.

And when we solve these equations, we find our unknown forces!

That's correct! Always pay attention that your reactions balance out and lead to a congruent result when working through statically indeterminate systems. Remember: *Balance through compatibility!*

To sum up, the combination of equilibrium equations and compatibility conditions allows us to find reactions in statically indeterminate structures.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore static determinacy, distinguishing between statically determinate and indeterminate structures. Reactions can be computed solely from geometry and load under static equilibrium. The significance and implications of having indeterminate structures are also discussed.
Detailed
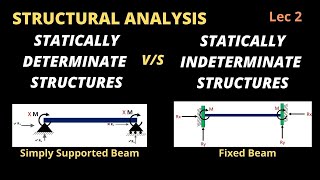
Static Determinacy
In structural analysis, static determinacy refers to the scenario where the reactions and internal forces in a structure can be determined using statics alone. This section examines how the reactions are solely a function of the structure's geometry, the types of boundary conditions, and the loads applied. When a structure is statically determinate, it means that the static equilibrium conditions (the equations for summation of forces and moments) are sufficient to solve for all reactions. Conversely, if the number of unknown reactions exceeds the number of equilibrium equations, the structure is classified as statically indeterminate. An illustration involving a rigid plate supported by multiple cables is presented, highlighting the method for determining stresses in statically indeterminate conditions, thus emphasizing the necessity of understanding compatibility of displacements in such scenarios.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Statically Determinate Structures
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In statically determinate structures, reactions depend only on the geometry, boundary conditions and loads.
Detailed Explanation
Statically determinate structures are those where you can compute all the forces acting on the structure based solely on its physical layout (geometry), the conditions at its supports (boundary conditions), and any external loads applied. This means that the structure has enough equations from the laws of equilibrium to solve for all unknown reactions without needing any additional information.
Examples & Analogies
Think of a simple seesaw balanced on a pivot. The weight on one side is directly countered by the weight on the other. If you know the weights, you can easily determine the forces without any extra calculations. Similarly, a statically determinate structure allows you to solve it directly with the information at hand.
Understanding Statically Indeterminate Structures
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If the reactions can not be determined simply from the equations of static equilibrium (and equations of conditions if present), then the reactions of the structure are said to be statically indeterminate.
Detailed Explanation
When a structure is statically indeterminate, it means that there are more unknown forces than can be solved using the available equations from static equilibrium alone. This typically happens when there are additional supports or constraints that complicate the analysis. In such cases, engineers must rely on other methods such as considering material properties and compatibility of deformations to find the solutions.
Examples & Analogies
Imagine trying to lift a heavy table that has a third leg in the middle. If you try to analyze just two legs, you won't account for how that third leg changes the forces acting on the table. This makes it harder to figure out how much weight each leg needs to hold up—just as with statically indeterminate structures, where the forces can't be simply calculated with basic equations.
Example Problem: Rigid Plate Supported by Cables
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A rigid plate is supported by two aluminum cables and a steel one. Determine the force in each cable. If the rigid plate supports a load P, determine the stress in each of the three cables.
Detailed Explanation
In this example, we have a rigid plate with three cables supporting it, leading to three unknowns (the forces in each cable) and only two independent equilibrium equations. This situation indicates that the problem is statically indeterminate because we cannot solve for all forces directly. To find the third necessary equation, we look at how the cables must deform equally when load P is applied, allowing us to relate the force in the cables through compatibility conditions.
Examples & Analogies
Imagine a friend trying to lift a large sign with three ropes. Two friends can easily pull on their ropes, but if they pull too hard without knowing the tension in the third rope, it might snap. If your friend doesn't analyze the forces correctly based on everyone's effort, the system fails. Similarly, understanding how connected parts of a structure share forces is crucial in determining the overall reaction forces.
Key Concepts
-
Static Determinacy: The property of a structure where all reactions can be determined solely through static equilibrium solutions.
-
Equilibrium Conditions: The conditions where the sum of forces and moments equals zero within a structure.
-
Statically Indeterminate Structures: Structures where more equations are needed to calculate responses due to excess unknowns.
Examples & Applications
A truss bridge where the connections allow for rotation and can be analyzed using static equilibrium equations.
A rigid plate suspended with multiple cables which requires consideration of compatibility of displacements to solve for cable tensions.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
For a structure to be at peace, its forces must sum to zero; only then will equilibrium cease.
Stories
Imagine a tightrope walker needing to balance. If too many ropes are attached, he cannot determine which pulls him; thus, he can't stay upright—a tale of static indeterminacy.
Memory Tools
Remember DICE: Determinate structures only use Internal conditions for calculation; Indeterminate needs Compatibility Equations.
Acronyms
INDY
Indeterminate Needs Degree of yield (compatibility) to solve.
Flash Cards
Glossary
- Static Determinacy
The condition of a structure where all reactions can be determined solely by static equilibrium equations.
- Statically Indeterminate
A structure in which the number of unknown reactions exceeds the available equilibrium equations.
- Equilibrium
A state where the sum of the forces and moments acting on a structure is zero.
- Compatibility of Displacements
The requirement that deformations in a structure lead to consistent changes in lengths of the members.
Reference links
Supplementary resources to enhance your learning experience.
