Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stiffness and Flexibility Method
Unlock Audio Lesson
Today, we will discuss the stiffness method and how it contrasts with the flexibility method in structural analysis. Can anyone tell me the main focus of the flexibility method?
It focuses on determining the unknown forces in a structure.
Exactly! The flexibility method seeks to find forces using displacement compatibility. Now, what about the stiffness method — what does it primarily focus on?
It focuses on calculating displacements instead of forces!
Correct! Remember, the stiffness method is all about defining relationships between forces and displacements based on equilibrium equations. A great acronym to remember this is SFD - Stiffness Defines Displacements.
So, is it true that structures can be both statically and kinematically indeterminate?
Good observation! Yes, static indeterminacy occurs with more unknown forces than available equilibrium equations. Kinematic indeterminacy relates to the independent displacements of a structure.
In summary, the flexibility method finds forces while the stiffness method focuses on displacements.
Degrees of Freedom and Static vs Kinematic Indeterminacy
Unlock Audio Lesson
Let’s delve into degrees of freedom as they relate to various structures. Can anybody provide examples of different structural types and their degrees of freedom?
Beams and trusses!
Exactly! 1D structures like beams focus on bending, while 2D trusses involve axial forces. They have specific degrees of freedom that tell us how many independent displacements can occur. How do you think this affects our analysis methods?
It means we have to account for more factors in kinematically indeterminate structures, right?
Absolutely! Kinematic indeterminacy implies we have more displacements to manage, making the analysis more complex but also crucial for accurate modeling.
To summarize, identifying the degrees of freedom is essential for determining whether a structure is statically or kinematically indeterminate.
Methods of Analysis
Unlock Audio Lesson
Let's explore the methods of analysis for stiffness-based problems. Who can name one of the methods?
The Slope Deflection Method?
That's right! The Slope Deflection Method helps resolve a system of linear equations based on displacements. Can anyone mention another method?
The Moment Distribution Method!
Exactly! It's iterative and can help figure out internal forces and displacements. However, the Direct Stiffness Method is one we must not forget—it’s highly efficient with computational analysis!
What makes the Direct Stiffness Method so powerful?
Great question! It simplifies the analysis into a matrix form, ideal for handling larger structures with ease. Just remember, the acronym 'DSM' stands for 'Direct Stiffness Method' to help you recall its importance.
In conclusion, familiarity with all three methods is vital for comprehensive structural analysis!
Kinematic Relations and Force-Displacement Relations
Unlock Audio Lesson
In this session, we’ll clarify the relationships between kinematic relations and force-displacement. How do we derive force relationships with displacements?
We use the relationships for individual elements instead of the entire structure?
Exactly! Focusing on individual elements helps simplify our calculations. Now, does anyone remember the equation associated with a beam's deflection?
It's the differential equation related to the moment and displacement!
Right you are! It shows how we can relate bending moments to displacements through integration. Always remember the equation's core components!
To summarize, establishing clear relationships of forces to displacements for individual elements leads to more comprehensive structural guidance.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section details two primary approaches to structural analysis: the flexibility method, which focuses on determining forces, and the stiffness method, which focuses on finding displacements. It highlights the conditions of static and kinematic indeterminacy and outlines three methods of analysis under the stiffness approach.
Detailed
Kinematic Indeterminacy; Stiffness Method
Introduction
The section provides insights into the fundamental concepts of kinematic indeterminacy and the stiffness method used in structural analysis.
1. Stiffness vs Flexibility
Two main categories of analysis methods are highlighted:
- Flexibility Method: Focuses on unknown forces and uses displacement compatibility to solve problems. Static indeterminacy arises when the number of unknowns exceeds the equations of equilibrium.
- Stiffness Method: Centers on unknown displacements, applying equilibrium equations to derive internal forces. The structure's degree of kinematic indeterminacy is defined by the total numbers of independent displacements.
2. Degrees of Freedom
Degrees of freedom apply to various structural systems including beams, trusses, and frames in 1D, 2D, and 3D analyses, indicating how many independent displacements can occur.
3. Methods of Analysis
Three established methods for conducting stiffness-based analysis:
- Slope Deflection Method: Produces a set of n linear equations for the n unknowns related to displacements.
- Moment Distribution Method: Iterative approach designed to calculate displacements and internal forces in bending structures.
- Direct Stiffness Method: A powerful technique framed in matrix form, suitable for computer analysis.
4. Kinematic Relations
The focus shifts to defining relationships between forces and displacements for individual elements versus the entire structure, utilizing concepts from the differential equations of beams to derive equations suited for structural analysis.
Youtube Videos
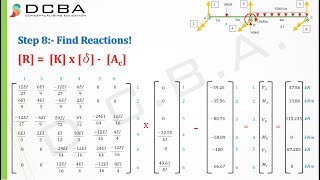
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Structural Analysis Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
There are two classes of structural analysis methods, Table 12.1:
1. Flexibility: where the primary unknown is a force...
2. Sti(cid:11)ness: method is the counterpart of the (cid:13)exibility one.
Detailed Explanation
In structural analysis, we have two main methods: Flexibility and Stiffness. The Flexibility method focuses on forces as the primary unknowns. It starts with equilibrium equations and addresses static indeterminacy when there are more unknown forces than equations. To resolve forces, it utilizes compatibility of displacements. In contrast, the Stiffness method centers around displacements as the primary unknowns. The approach begins with expressing forces in terms of displacements, essentially treating the entire structure as kinematically indeterminate based on its independent displacements. In both methods, understanding these foundational concepts is crucial as they determine how engineers approach and solve structural problems.
Examples & Analogies
Think of a suspension bridge. Engineers need to know how much weight it can hold (forces) and how much it will sway or move with that weight (displacements). Using the Flexibility method is like focusing on how much you can load the bridge, while the Stiffness method is like figuring out how much it will flex or sway under that load.
Flexibility and Stiffness Characteristics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Flexibility Sti(cid:11)ness
Primary Variable (d.o.f.) Forces Displacements
Indeterminancy Static Kinematic
Force-Displacement... Governing Relations Compatibility of displacement Equilibrium
Detailed Explanation
This table differentiates the two methods in terms of primary variables (degrees of freedom), indeterminacy types, and governing relations. In the Flexibility method, the main variable is force, making it a static method; the governing relation is compatibility of displacements. Conversely, in the Stiffness method, displacements are the primary variable, making it a kinematic method, where the governing relation is equilibrium. By understanding these distinctions, students can grasp how different structural situations might require a specific analytical approach.
Examples & Analogies
Imagine you're adjusting a tightrope walker. If you think about the force they exert to stay upright, that's like the Flexibility method. But if you're focused on how they sway from side to side, that's akin to the Stiffness method. Each perspective offers valuable insights into their balancing act.
Methods of Analysis in Stiffness-based Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
There are three methods for the sti(cid:11)ness based analysis of a structure:
1. Slope De(cid:13)ection...
2. Moment Distribution...
3. Direct Sti(cid:11)ness method...
Detailed Explanation
In stiffness-based analysis, there are three primary methods. The Slope Deflection method leads to a system of equations with unknown displacements, making it suitable for manual calculations. The Moment Distribution method is iterative and particularly effective for analyzing beams and frames. Finally, the Direct Stiffness method, articulated in matrix form, is the most powerful and flexible, often utilized in computer-based analyses. Each method provides a different approach to solving the same structural problems, allowing engineers to select the most efficient method based on the problem's complexity.
Examples & Analogies
Consider a group of friends trying to coordinate a project. The Slope Deflection method is like each friend suggesting how much work they'll do individually, creating a plan together. The Moment Distribution method is akin to everyone taking turns refining the overall plan based on group feedback. The Direct Stiffness method, however, is like using a project management app that organizes everyone's inputs and tasks automatically, ensuring everything runs smoothly.
Understanding Force-Displacement Relations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Whereas in the (cid:13)exibility method we sought to obtain a displacement in terms of the forces...
Detailed Explanation
Force-displacement relations form a critical part of understanding structural mechanics. In the Flexibility method, the focus is on expressing displacements based on applied forces. However, in the Stiffness method, we reverse that approach, establishing how internal forces relate to known displacements in a structural element. It’s essential for engineers to derive accurate relations for effective analysis and design, especially when dealing with complex structures.
Examples & Analogies
Think about a spring. When you pull or compress it, the amount of stretch or compression directly corresponds to the force you apply (Hooke's law). Understanding the relationship between the force you apply and the spring’s displacement is crucial whether you're designing a car shock absorber or a new toy.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Static Indeterminacy: More unknown forces than equilibrium equations.
-
Kinematic Indeterminacy: Refers to independent displacements in a structure.
-
Degrees of Freedom: Independent movements or displacements within structures.
-
Stiffness Method: Focused on determining displacements through relationships of forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a truss system, determine the displacements at each joint to find internal forces using the stiffness method.
-
For a continuous beam experiencing a moment at its center, apply the slope deflection method to derive resultant forces based on the calculated deflections.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flexibility deals with force, to find the bends is its course. Stiffness needs displacements true, for structure strength it will pursue.
📖 Fascinating Stories
-
Once a bridge wanted to know, if it was force or bends that would show. It learned from stiffness, which means to sway, keep forces balanced at the end of the day!
🧠 Other Memory Gems
-
SFD - Slope For Displacement, remember to calculate moments when forces rest.
🎯 Super Acronyms
DSF - Direct Stiffness Formula helps compute complexity in forms of structures.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Flexibility Method
Definition:
An approach to structural analysis where unknown forces are calculated, focusing on compatibility of displacements.
-
Term: Stiffness Method
Definition:
A structural analysis approach focusing on calculating displacements, with internal forces derived from these displacements.
-
Term: Static Indeterminacy
Definition:
A condition where there are more unknown forces than equilibrium equations available to solve them.
-
Term: Kinematic Indeterminacy
Definition:
Refers to the number of independent displacements in a structure, indicating how many degrees of freedom exist.
-
Term: Degrees of Freedom
Definition:
The number of independent movements or displacements that a structure can undergo.