Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Moment Distribution Method
Unlock Audio Lesson
Today, we're diving into the moment distribution method, an iterative technique for solving statically indeterminate structures. Can anyone tell me why we need this method?
We need it because some structures have more unknown forces than equations!
Exactly! This method helps us handle those extra unknowns by balancing internal moments. Now, let's outline the process. What’s the first step?
We calculate the fixed-end moments based on applied loads.
Right! We start with fixed-end moments. Remember, they form the basis for our subsequent calculations. Let's also remember the acronym 'FEM' for Fixed-End Moments!
What do we do after finding those moments?
After that, we perform a balancing operation at the joints. What does balancing involve?
Adjusting the moments until they equal zero at each joint!
Correct! It’s important to emphasize no joint translation during this process. To recap, we first find the fixed-end moments, then adjust through balancing until equilibrium is reached. Let’s proceed to our example!
Application of the Moment Distribution Method
Unlock Audio Lesson
In our example, we analyze a continuous beam with initial settlement at one support. Who can remind us why settlements affect our analysis?
Settlements change how loads are distributed in the structure!
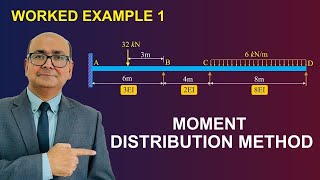
Exactly! We need to consider that while calculating moments. Let’s start with the fixed-end moments based on a uniform load. What’s the formula we use?
We use MF = (wL²) / 12 for each end!
Great! Now, use that to find the moments at our beam's ends. Once we have those, what do we do next?
We enter the moments into our balance table and work through adjustments.
Correct! And as we adjust our moment values, we keep an eye out for translations. Remember, the adjustments ultimately express the behavior of our entire structure. Let’s visualize this with our step-by-step moment distribution table.
Final Steps and Confirmation of Equilibrium
Unlock Audio Lesson
Now, after going through our moment distribution, how do we confirm that we’ve achieved equilibrium?
We check that the sum of moments around each joint equals zero!
Exactly! It's crucial to validate that no unintended translations occurred. Let’s think about what happens if they do. What could be the consequence?
It could lead to miscalculating moments and unsafe designs!
Right! Safety is paramount in structural engineering. So, our final moment values should accurately represent the structure's internal forces under those loads. As a memory aid, think 'Balanced Moments, Safe Structures' when applying this method!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The moment distribution method is an iterative technique used to find internal moments in continuous beams and frames. In this section, key concepts are introduced, including fixed-end moments, the balancing operation, and the necessity of ensuring that no translation occurs during moment adjustments. The significance of the method is highlighted through practical applications and examples.
Detailed
Moment Distribution; Indirect Solution
The moment distribution method, developed by Cross in 1930, is an iterative solution for determining moments in structural systems that are statically indeterminate. The process begins by calculating the fixed-end moments created by external loads, which are then adjusted through a series of balancing operations as the joints of the structure are allowed to rotate.
Key Concepts
- Fixed-End Moments: The starting point involves the calculation of fixed-end moments which arise from the external loads on the beam or structural frame.
- Balancing Operation: This procedure adjusts the internal moments at the ends of the members until equilibrium is reached at each joint, ensuring that the sum of moments around each joint equals zero.
- No Joint Translation: Throughout this balancing, it is critical to restrict any translation of joints to accurately simulate real conditions under load.
Example Application
The section provides an example illustrating these steps through a continuous beam subject to an initial settlement. The analysis is detailed, including fixed-end moment calculations, subsequent moment distribution among various members, and adjustments required to achieve balance. The example culminates in determining internal distributions while confirming that joint rotations are appropriately accounted for in the final moment distribution results. This methodology ensures that engineers can accurately design and assess the behavior of more complex structures under load.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Moment Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The first step is to perform the usual moment distribution. The reader should fully understand that this balancing operation adjusts the internal moments at the ends of the members by a series of corrections as the joints are considered to rotate, until (ΔM) = 0 at each joint. The reader should also realize that during this balancing operation no translation of any joint is permitted.
Detailed Explanation
In moment distribution analysis, the first step involves adjusting the internal moments at the ends of a structure's members. This is done through a balancing process where we consider how joints rotate until the moment changes (ΔM) at each joint equal zero. This ensures that we accurately represent the internal forces without allowing the joints to move out of position, maintaining the structure's overall integrity.
Examples & Analogies
Think of it like balancing a seesaw. Each time one side goes down due to weight, you need to add or remove weight from the other side to keep it level. In a structural sense, we're making adjustments to ensure that the entire structure remains stable and balanced.
Calculating Fixed-End Moments
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The fixed-end moments are
(18)(12)(62) MF = +24 k.ft (12.71-a)
(18)(6)(122) MF = 48 k.ft (12.71-b)
Detailed Explanation
To calculate the fixed-end moments for the structural members, we use specific load calculations. The equations provided give us the moments at the fixed ends when considering uniform loads. For instance, the first equation results in a fixed-end moment of +24 k.ft for the moment at one end of a member, while the second equation gives +48 k.ft for a different member.
Examples & Analogies
Imagine an anchor holding a boat steady in the water. The fixed-end moments are like the forces that hold the anchor in place, ensuring that despite any disturbances (like waves or wind), the boat does not move from its position.
Moment Distribution Process
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
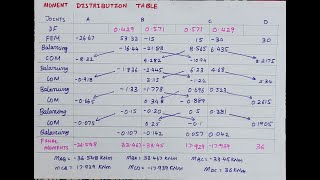
- Moment distribution
Joint A B C D Balance CO
Member AB BA BC CB CD DC
K 10 10 20 20 15 15
DF 0 0.333 0.667 0.571 0.429 0
FEM +24.0 -48.0 FEM
+13.7 +27.4 +20.6 +10.3 C DC; BC
-6.3 -12.6 -25.1 -12.5 B AB; CB
+3.6 +7.1 +5.4 +2.7 C BC; DC
-0.6 -1.2 -2.4 -1.2 B AB; CB
+0.3 +0.7 +0.5 +0.02 C BC; DC
Total -6.9 -13.9 +13.9 -26.5 +26.5 +13.2
Detailed Explanation
The table outlines the moment distribution process across different joints (A, B, C, D) and members. It starts by identifying the fixed-end moments (FEM) and then computing moment corrections. Each joint adjusts its moment based on the contribution of each member connected to it until an equilibrium is reached, where the total moment balance equals zero. The K values represent coefficients based on the structural configuration, while doubling down on these adjustments helps achieve the state of equilibrium.
Examples & Analogies
Consider a group of friends lifting a table. Each friend has to push at the right force to keep the table steady and balanced. If one friend is pushing harder than others, the table will tip. In moment distribution, each 'push' is like a moment correction helping the structure remain stable, preventing it from tipping over.
Understanding Side-Sway Corrections
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The final moments listed in the table are correct only if there is no translation of any joint. It is therefore necessary to determine whether or not, with the above moments existing, there is any tendency for side lurch of the top of the frame.
Detailed Explanation
The final calculated internal moments are deemed valid only if the structure does not translate, meaning that the joints do not move horizontally or vertically. After calculating these moments, it is essential to check if the structure may exhibit any lateral movement (side-sway). This assessment ensures that the internal force changes contribute to a stable structure without unintended shifts.
Examples & Analogies
Think of a tall tower. If the ground beneath shifts or if there’s wind pressure, the top of the tower might sway. Engineers must ensure that all forces are aligned to keep the tower standing straight. In this context, checking for side-sway corrections is akin to ensuring the tower remains perfectly vertical despite external influences.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fixed-End Moments: The starting point involves the calculation of fixed-end moments which arise from the external loads on the beam or structural frame.
-
Balancing Operation: This procedure adjusts the internal moments at the ends of the members until equilibrium is reached at each joint, ensuring that the sum of moments around each joint equals zero.
-
No Joint Translation: Throughout this balancing, it is critical to restrict any translation of joints to accurately simulate real conditions under load.
-
Example Application
-
The section provides an example illustrating these steps through a continuous beam subject to an initial settlement. The analysis is detailed, including fixed-end moment calculations, subsequent moment distribution among various members, and adjustments required to achieve balance. The example culminates in determining internal distributions while confirming that joint rotations are appropriately accounted for in the final moment distribution results. This methodology ensures that engineers can accurately design and assess the behavior of more complex structures under load.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating the fixed-end moments for a beam subjected to a uniform load.
-
Performing the moment distribution method iteratively to determine the internal moments.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In beams that bend and sway, fixed moments guide the way.
📖 Fascinating Stories
-
Imagine a builder who must make sure his structure stands without wobbling; he checks his fixed-end moments before allowing any changes to keep it steady.
🧠 Other Memory Gems
-
Balance Each Joint to Ensure Moment Equal is a way to remember the balancing operation in the method.
🎯 Super Acronyms
FEM stands for Fixed-End Moment, helping recall its significance in moment calculations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: FixedEnd Moments (FEM)
Definition:
Moments induced in a member when both ends are fixed and subjected to loads.
-
Term: Moment Distribution
Definition:
An iterative method used to calculate internal moments in statically indeterminate structures.
-
Term: Equilibrium
Definition:
A state in which all forces and moments acting on a structure result in a net force and moment of zero.