Elastic Buckling
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Slenderness Parameter
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to discuss the slenderness parameter, denoted as ℓ. Can anyone tell me why we need such a parameter in column analysis?

It's to evaluate how columns behave under compression, right?

Exactly! This parameter helps us assess both the slenderness ratio and the material properties of steel columns. When we look at elastic buckling, this parameter becomes crucial. Remember this: ℓ integrates various factors. Can anyone think of reasons we'd prefer this over the standard slenderness ratio?

Maybe because it gives a more comprehensive view of how the column will perform?

Great observation! Inelastic buckling requires a different approach, especially when gross yielding occurs.

To help you remember this concept, think of the acronym PACE: Parameter Accounts for Column Elasticity.

So, does inelastic buckling only apply when the parameter is lower?

Correct! And we'll find more on that in our other discussions today.

To summarize, the slenderness parameter is essential in differentiating between inelastic and elastic buckling. Keep that in mind!
Elastic versus Inelastic Buckling
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's differentiate between elastic and inelastic buckling. Who can summarize the distinction between the two types?

Elastic buckling deals with the initial failure, while inelastic buckling considers material yielding?

Exactly! When we talk about the equations, we have two forms: one for inelastic buckling and one for elastic buckling. Can anyone recall the form of Euler's equation?

I think it's F_cr = π²EI/(KL)².

Correct! And when ℓ is greater than π², we apply that Euler equation. Remember that we also have the equation for inelastic buckling, where F_cr = 1/ℓ² for ℓ ≤ π². To remember which is which, think 'E for Elastic!'

And how does this impact our designs?

Great question! These equations inform our structural design choices. Now, let’s wrap this up: elastic buckling focuses on initial deflection, while inelastic buckling addresses yielding. Both are essential for structural safety and efficiency.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section elaborates on the slenderness parameter (A) and its significance in assessing buckling behavior of steel columns. It distinguishes between elastic and inelastic buckling through key equations, providing insights into design considerations under LRFD provisions.
Detailed
Elastic Buckling
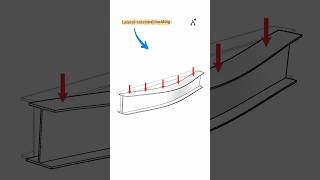
In this section, we explore the fundamental concept of elastic buckling in steel compression members, as governed by the LRFD provisions. The slenderness parameter, denoted as ℓ, is introduced to effectively analyze and design steel columns. This parameter integrates both the slenderness ratio and material properties to determine buckling behavior. The equations presented demarcate inelastic buckling, characterized by gross yielding, distinctly from elastic buckling, where Euler's critical load applies. The section concludes by emphasizing the implications of these equations for concentrically straight members, critical for structural integrity and safety.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Slenderness Parameter
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
By introducing a slenderness parameter (\(\psi\)) (not to be confused with the slenderness ratio) defined as
\[\psi^2 = \frac{F_y}{F_{cr}} = \frac{K L}{r_{min}}\]
Hence, this parameter accounts for both the slenderness ratio as well as steel material properties. This new parameter is a more suitable one than the slenderness ratio (which was a delimiter for elastic buckling) for the inelastic buckling.
Detailed Explanation
The slenderness parameter (\(\psi\)) is a critical value that helps analyze the stability of steel columns under compression. It differs from the slenderness ratio, which only considers the shape of the column. While the slenderness ratio indicates potential buckling behavior, the slenderness parameter includes both the ratio and material properties, enhancing the analysis accuracy especially for scenarios of inelastic buckling where the material begins to yield.
Examples & Analogies
Think of the slenderness ratio like measuring a tall, thin tree. Knowing how tall it is compared to its width gives some idea about its stability against the wind. However, adding information about its wood quality (the material properties) would give a better picture—like knowing if the wood is strong or weak. This combined understanding is what the slenderness parameter achieves.
Equations for Critical Stress
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Equation 19.2 becomes
\[F_{cr} = \frac{1}{3} F_y \psi^2\text{ for } \psi \leq \sqrt{2}\]
When \(\psi > \sqrt{2}\), then Euler equation applies:
\[F_{cr} = \frac{F_y}{\psi^2}\text{ for } \psi > \sqrt{2}\]
Detailed Explanation
These equations determine the critical stress at which buckling occurs. The first equation applies to lower slenderness parameters (\(\psi\) less than or equal to \(\sqrt{2}\)), indicating inelastic buckling where material yielding may take place. The second equation applies when the slenderness exceeds a certain threshold, utilizing Euler's formula which assumes that the material can withstand elastic buckling without yielding. These formulas allow engineers to design safe and effective structures.
Examples & Analogies
Imagine a pencil: if you push down gently, it can flex (inelastic buckling) without breaking. But if you push down too hard, a certain point is reached (elastic buckling), where it will bend dramatically and may fail. The equations help predict these moments more accurately.
Relationship Between Inelastic and Elastic Buckling Curves
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Hence the first equation is based on inelastic buckling (with gross yielding as a limiting case), and the second one on elastic buckling. The two curves are tangent to each other.
Detailed Explanation
This chunk highlights the connection between the inelastic and elastic buckling responses of steel columns. As the slenderness parameter increases, there is a transition between the two states of behavior. The curve representing inelastic buckling meets the elastic buckling curve at a certain point, indicating that as the slenderness increases, the type of buckling that occurs can shift from one to the other, which is crucial for understanding failure modes in structural design.
Examples & Analogies
Think of it like a bicycle tire: When over-inflated, it may bulge (inelastic behavior), but once more pressure is applied (exceeding the limits), it might burst suddenly (elastic behavior). The transition point is where the tire’s material can no longer handle the stress.
Application to Concentrically Straight Members
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The above equations are valid for concentrically straight members.
Detailed Explanation
This statement indicates that the derived equations for critical stress are applicable only to straight members that are subjected to axial loads. If the member is not straight or experiences eccentric loading (where the load does not act through the centroid), then additional considerations are necessary to accurately predict buckling behavior. Understanding the limitations of these equations is important for correct engineering applications.
Examples & Analogies
Consider a perfectly straight flagpole in the wind: it can be analyzed simply with these equations. However, if the pole leans or if the wind blows unevenly, it’s like trying to analyze a crooked tree in a storm; it requires a different approach for understanding how it will behave.
Key Concepts
-
Slenderness Parameter: A crucial measure for assessing buckling behavior beyond the slenderness ratio in steel columns.
-
Elastic Buckling: The type of buckling before yielding occurs, governed by Euler's critical load equation.
-
Inelastic Buckling: Post-yield bucking that considers the yielding material, needing a different approach for calculations.
Examples & Applications
In designing a tall steel column, calculating the slenderness parameter helps determine whether elastic or inelastic buckling will dominate.
When assessing a column's stability, engineers must refer to the relevant equations to evaluate the load it can safely carry without buckling.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
For columns tall and wide, the slenderness must guide; buckle not in elastic pride!
Stories
Imagine a tall tower. The engineer checks the slenderness parameter carefully, ensuring it stays safe from the threat of buckling, avoiding disaster!
Memory Tools
E.I. for Elastic; I.P. for Inelastic – E before I for their sequence in failure.
Acronyms
B.E.S.T.
Buckling Elastic versus Slenderness and Tensile behavior of materials.
Flash Cards
Glossary
- Slenderness Parameter
A parameter that combines slenderness ratio and material properties for assessing buckling behavior in steel members.
- Elastic Buckling
The mode of buckling that occurs before any yielding of the material takes place.
- Inelastic Buckling
Buckling that occurs post-yielding, where the material exhibits plastic deformation.
Reference links
Supplementary resources to enhance your learning experience.
