Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
By Ordinates from the Long Chord
Unlock Audio Lesson
Today, we're discussing the method of setting out curves by ordinates from the long chord. This technique is fundamental to ensuring our curves are accurate. Can anyone tell me what we understand by a 'long chord'?
I think it's the straight line connecting two points on the curve.
Exactly! The long chord connects the endpoints of our curve. Now, what do we do with that chord to set out the curve?
We create offsets, right? Like perpendicular lines from the chord?
Correct! These offsets allow us to establish points along the curve. Now, can anyone summarize how we calculate those offsets?
We use formulas based on the radius, the length of the chord, and the distance from the midpoint.
Good job! Remember the equation O = √ (R² − x²) helps you find offsets accurately. Always visualize this relationship!
In summary, this method requires dividing the chord into equal sections, calculating offsets, and using them to establish points along the curve. Be sure to practice these calculations!
By Successive Bisection of Arcs
Unlock Audio Lesson
Now, let's look at the successive bisection of arcs. Who recalls what this method entails?
Isn't it about bisecting chords? We also use the versine to find offsets.
That's right! In this method, we bisect not just the chords but the arcs of the curve too. This aids in accurately plotting points even when the ground is difficult to measure. Can someone explain what a versine is?
It's the distance from the chord to the arc, right?
Yes, well done! As a helpful mnemonic, remember that 'versine' is 'vertical sine.' This makes it easier to connect the concept to the geometry involved. What are the steps you would take to apply this method?
We start by bisecting the initial chord, setting points using the versine value, then repeating this for subsequent segments.
Perfect! Make sure to practice these steps. To wrap up, remember that this method is beneficial when other ground measuring methods are impractical.
By Offsets from Tangents
Unlock Audio Lesson
Next, let's explore setting out curves by offsets from the tangents. Can anyone explain what the two types of offsets are?
We have radial offsets and perpendicular offsets.
That's correct! Radial offsets are measured directly outward from the tangent, while perpendicular offsets are at right angles. What are some formulas we might use with these offsets?
For radial offsets, we can use PP = OP - OR where each is calculated based on the radius.
Exactly! And don't forget for large radii, approximation formulas can help simplify calculations too. Now, how do we implement these steps in a real-world scenario?
We need to locate tangent points, then measure distances and apply the formulas for offsets we've learned.
Well said! In summarizing this method, remember it is especially useful for sharp curves where measurements need to be precise. Always pay attention to the ground conditions!
By Offsets from Chords Produced
Unlock Audio Lesson
Lastly, let's discuss setting out curves using offsets from chords that are produced. What do you think is meant by 'chords produced'?
I believe it means extending the chord beyond the curve to find offset points.
Exactly! This allows for greater flexibility when locating points on the curve. What are some considerations we should take into account with this method?
We need to ensure we properly calculate the angle subtended at the center to maintain accuracy.
That’s a great observation! And can anyone recap how to practically apply this method step by step?
First, locate the tangent points, then calculate the lengths of chords and their offsets, ensure to consider any angles involved, then complete the setup!
Wonderful! To conclude this session, remember that this method is beneficial when precise measurements are required across the curve.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
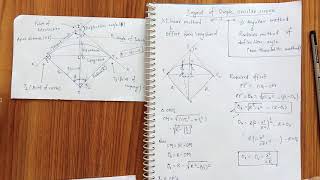
The section discusses methods for setting out simple circular curves, emphasizing linear techniques such as ordinates from the long chord, successive bisection of arcs, offsets from tangents, and offsets from chords produced. Each method is explained with procedural steps and mathematical formulations.
Detailed
Linear Methods of Setting Out Curves
This section explains four linear methods utilized for setting out simple circular curves in construction projects. Understanding these methods is crucial for engineers and surveyors when designing roadways, railways, and other infrastructure involving curves. The methods discussed include:
- By Ordinates from the Long Chord: This method involves establishing points along a curve by erecting perpendicular offsets from a long chord, which allows for precise calculations when determining offsets and positions on the curve. The offsets can be accurately calculated using relationships derived from the properties of circles.
- By Successive Bisection of Arcs (Versine Method): This technique entails bisecting the arcs of the curve to determine offset points. It is particularly useful when accurate measurements of the ground distance outside the curve are challenging to obtain.
- By Offsets from the Tangents: This method utilizes radial or perpendicular offsets from the tangents of the curve to plot points accurately. Two approaches—radial offsets and perpendicular offsets—are detailed, with specific formulas for each scenario.
- By Offsets from Chords Produced: This involves taking offsets from extended or produced chords to define the curve accurately and calculate offsets effectively.
Overall, these methods are essential for ensuring that curves in road construction are set out accurately, facilitating safe and efficient design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Linear Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
(a) Linear methods of setting out curves
The following methods of setting out simple circular curve are linear as measurement is done using chain/tape/distance/EDM:
1. By ordinates from the long chord
2. By successive bisection of arcs
3. By offsets from the tangents
4. By offsets from chords produced
Detailed Explanation
This section introduces the topic of linear methods used to set out circular curves in surveying. These methods rely on physical measurements using tools like chains or tapes rather than angular calculations. The methods listed include:
1. Using ordinates from the long chord.
2. Successive bisections of arcs.
3. Offsets from the tangents.
4. Offsets from chords produced. Each of these methods allows surveyors to determine points along a curve accurately.
Examples & Analogies
Imagine planning a road that bends smoothly. Surveyors use various methods to measure where to place the road markers. Using a long piece of string (the long chord), they compute where to place each marker based on measurements. This is similar to how a gardener lays out a curved flower bed using stakes and ropes.
Method 1: By Ordinates from the Long Chord
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
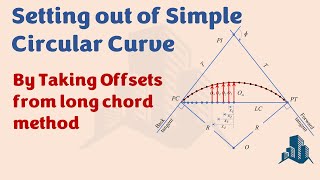
- By ordinates from the long chord:
In this method, the perpendicular offsets are erected from the long chord to establish points along the curve, as shown in Figure 2.5. If T T is the length of the long chord (L), ED = O which is the offset at mid-point (E) of the long chord (the versine), and PQ = O which is the offset at distance x from E. Draw a line QQ parallel to T T which meets OD at Q, and line OQ which cuts T T at point E.
Detailed Explanation
This method involves setting offsets from a straight line called the long chord to locate points on the circular curve. The offsets indicate how far each point on the curve deviates from the chord. The process uses the relationship of various points along the chord and curve to calculate distances accurately. It helps to establish several points along the curve symmetrically, making it easier to layout short curves, such as street bends.
Examples & Analogies
Think of laying tiles in a curved design. The straight lines are the long chord. You place a ruler to see how far out from the ruler (long chord) each tile (offset) should be to create a perfect curve. By measuring offsets, you can get a nice smooth edge where the tiles meet.
Method 2: By Successive Bisection of Arcs
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- By successive bisections of arcs:
It is also known as Versine method. In Figure 2.6, a curve T DT is to be established on the ground by this method. The steps involved are -
(i) Join T T and bisect it at E. Set out the offset ED (which is equal to the versine R(1- cos(𝜙/2)), thus a point D on the curve may be fixed.
(ii) Join T D and DT and bisect them at F and G, respectively. Then set out the offsets FH and KG at F and G, respectively, in the same manner, each equal to R(1- cos(𝜙/4)). Thus, two more points H and K are fixed on the curve.
Detailed Explanation
The successive bisection method, also known as the Versine method, works by continually dividing the arc into smaller sections to find points along the curve. Starting at the chord endpoints, it finds the midpoint and uses geometrical calculations based on known properties of circles to create additional points along the curve. Each step involves measuring offsets based on the bisected arcs, allowing for precision in reaching the desired curve shape.
Examples & Analogies
Imagine slicing a pizza. If you want to find where to place the toppings evenly, you cut the pizza into halves, then those halves into quarters, and so on. Just like that, each bisection helps to mark exactly where the decorations should go to make the pizza (or curve) perfect.
Method 3: By Offsets from the Tangents
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
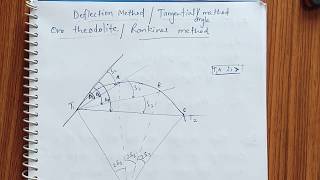
- By offsets from the tangents: The offsets may be either radial or perpendicular to the tangents.
(a) By radial offsets
In Figure 2.7, if O = PP which is the radial offset at P from O at a distance of x from T along the tangent AB, then - PP = OP – OP where OP = R^2 + x^2 and OP = R. O = R^2 + x^2 - R (Exact).
Detailed Explanation
This method uses offsets measured from tangent lines that intersect the curve. The offsets can be radial (pointing directly toward the center of the curve) or perpendicular from the tangential line. Using geometrical properties of circles, surveyors can calculate how far along the tangents they need to measure to correctly represent points along the curve. It is convenient for sharp curves where ground measurement is straightforward.
Examples & Analogies
Picture a bicycle that's navigating around a sharp corner. The handlebars can be thought of as the tangents, guiding where to go. By knowing how far you need to pull the handlebars outward (offsets), you can ensure that the bike stays on track along the curve.
Method 4: By Offsets from Chords Produced
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- By offsets from chords produced. In Figure 2.9, if AB is the first tangent, T is the first tangent point, E, F, G etc., are the successive points on the curve. Draw arc EE , so T E= T E = C which is the first chords. Similarly, EF, FG, etc., are successive chords of length C , C etc., each being equal to the full chord length.
Detailed Explanation
Offsets from chords produced involve extending the lines from tangent points into the curve. As new chords are introduced, offsets from these chords are calculated to create a smooth, curved trajectory. This method tends to produce large, sweeping curves and establishes points along the arcs based on already calculated chord lengths. It facilitates laying out long curves effectively.
Examples & Analogies
Think of drawing a large arc with a compass. Each time you place a new point along the drawn arc, it's like extending the chord and measuring how far outward it goes. This helps to maintain a smooth curve for whatever beautiful design you're creating.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Ordinates from Long Chord: A method to measure offsets for curve construction.
-
Bisection of Arcs: Successive bisection helps in accurate point placement.
-
Offsets from Tangents: Use of both radial and perpendicular offsets allows for flexibility.
-
Offsets from Chords: Utilizing produced chords can aid in flexibility in design.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of setting out a street curve using the ordinates method.
-
Applying the versine method in determining the offsets on a railway curve.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Chords are straight, curves are round, put them together, measurements abound!
📖 Fascinating Stories
-
Imagine a road lined with trees, where engineers must plan the curves around hills. They measure chords and calculate offsets, ensuring every turn is safe and smooth.
🧠 Other Memory Gems
-
Use 'COVERS' to remember: Chord, Offsets, Versines, Engineering Road Safety.
🎯 Super Acronyms
R.O.C. for Radial, Offsets, and Chords to recall key methods of setting out curves.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Long Chord
Definition:
A straight line connecting the endpoints of a circular curve.
-
Term: Offsets
Definition:
Perpendicular lines from the chord or tangent to establish points on the curve.
-
Term: Versine
Definition:
The distance from the chord to the arc of a circle.
-
Term: Radial Offsets
Definition:
Offsets measured radially outward from a point on a tangent.
-
Term: Perpendicular Offsets
Definition:
Offsets taken at right angles from the tangent line to the curve.