Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Triangulation
Unlock Audio Lesson
Today, we'll discuss triangulation surveys, which are essential for accurate surveying. Can anyone tell me what triangulation means in a surveying context?
Isn't it about using triangles to find locations or distances?
Correct! Triangulation uses triangles, specifically, if you know one side and two angles, you can calculate the other sides. This method is vital in establishing control points. Let's remember this with the acronym 'TAC' for Triangles, Angles, and Control points.
What are control points?
Control points, or triangulation stations, are the locations where we measure angles. They form the vertices of our triangles. To visualize this, think of a map where each point connects to create a layout.
And why do we use them in engineering projects?
Great question! We use triangulation to ensure accuracy in placing structures like bridges because even a small error can lead to significant issues in construction.
Factors in Station Selection
Unlock Audio Lesson
Let's now discuss the factors for selecting triangulation stations. Why do you think we consider the angles when choosing a location?
It must be because certain angles give better accuracy?
Exactly! We prefer angles between 30° and 120°, with isosceles triangles being optimal at 56° 14'. Remember: 'Optimal Angles = OPA' - angle variation helps maintain precision.
What about the visibility aspect?
Visibility is crucial. We want clear lines of sight, especially on high points like hills. Always ensure stations are inter-visible. So, in short, ensure visibility, good angles, and accessibility.
Trilateration vs. Triangulation
Unlock Audio Lesson
Now, let’s compare triangulation with trilateration. What’s the key difference?
Triangulation uses angles and sides, while trilateration measures only the sides?
Exactly! Trilateration involves measuring distances, then computing angles, which can sometimes be more efficient. It's useful in modern surveying, especially since technology has made it easier to measure distances accurately.
Why choose one method over the other?
Triangulation might be better for smaller areas, while trilateration suits larger terrains. Always consider the project requirements and terrain when choosing your method.
Accuracy and Corrections
Unlock Audio Lesson
Accuracy is critical in triangulation surveys. Can anyone list some factors that affect accuracy?
I think the baseline length and angles could affect the outcomes.
Correct! For very long baselines, we also need to apply corrections to maintain accuracy, such as temperature and tension corrections. Remember the mnemonic 'BAT' for Baseline adjustments necessary.
How do we check if the triangulation was accurate?
We do closure checks by measuring known distances again to ensure calculations align. Always verify accuracy through repeated measures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into triangulation surveys as a method for establishing accurate control in surveying by using the geometric properties of triangles. The process measures baselines and angles to compute positions, contributing to fields such as geodesy and civil engineering.
Detailed
Triangulation Surveys
Triangulation is a vital method in surveying focused on establishing precise control points through a network of triangles. The fundamental principle relies on the trigonometric property that if one side (the base) and two angles of a triangle are known, the remaining sides can be calculated. The series of triangles formed is interconnected through control points known as triangulation stations.
The primary applications of triangulation surveys include:
- Establishing accurate control for plane and geodetic surveys,
- Determining the Earth's size and shape,
- Marking precise locations for civil engineering projects including bridges and tunnels.
Choosing suitable positions for control stations is crucial. It involves an assessment to ensure connectivity and stability of intervisibility among stations, utilizing existing maps with contour data for guidance. The section outlines critical factors that influence the selection of stations, including triangle shape, angle measurements, and visibility conditions.
Additionally, the content distinguishes triangulation from trilateration, where distances are measured instead of angles, which can lead to high accuracies in various surveying applications. Knowing the principles of triangulation supports efficiency in both fieldwork and computational efforts, vital for conducting expansive surveys and ensuring quality engineering outcomes.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Triangulation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Triangulation is one of the methods of fixing accurate controls. It is based on the trigonometric proposition that if one side and two angles of a triangle are known, the remaining sides can be computed. A triangulation system consists of a series of triangles in which the long side is normally called the base line. The base line is measured and remaining sides are calculated from the angles measured at the vertices of the triangles; vertices, being the control points, are called triangulation stations.
Detailed Explanation
Triangulation is essentially a method used in surveying to determine precise locations on the Earth. By knowing just one side (the base line) of a triangle and the angles at the other two vertices, one can use trigonometry to find out the lengths of the other two sides. This is particularly useful for creating a network of control points that can be referenced for further measurements.
Examples & Analogies
Imagine you are in a large open field with a tent (representing a triangulation station) and you want to measure the distances to two trees at known angles. By measuring the distance to the tent (the base line) and the angles to the trees, you can use triangular calculations to find out how far each tree is from the tent.
Applications of Triangulation Surveys
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications of triangulation surveys include; (i) establishment of accurate control for plane and geodetic surveys as well as photogrammetric surveys covering large areas, (ii) determination of the size and shape of the Earth, and (iii) determination of accurate locations for setting out of civil engineering works.
Detailed Explanation
Triangulation surveys are used in several significant ways. They help establish control points for mapping large areas accurately and can also determine Earth's dimensions, which is crucial for global positioning systems and geographical studies. Additionally, triangulation provides precise locations for engineering projects such as bridges and tunnels, ensuring that construction is accurate and reliable.
Examples & Analogies
Think of triangulation as the blueprint for a large building. Just as the blueprint ensures that every part of the building is in the right place, triangulation helps ensure that every part of a large engineering project is built accurately according to the plan.
Choosing Triangulation Stations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The area to be covered by a triangulation scheme must be carefully studied to select the most suitable positions for the control stations. Factors to consider include: the best shape of a triangle, ensuring intervisibility, and accessibility to the stations.
Detailed Explanation
Choosing where to place triangulation stations is crucial for the accuracy and efficiency of a triangulation survey. Ideally, stations should form shapes that minimize error, such as isosceles or equilateral triangles, and should be positioned in locations where they can see each other clearly (intervisibility). Additionally, it's important to ensure that these stations are easily accessible for surveyors who will need to set up equipment.
Examples & Analogies
Imagine setting up a treasure hunt in a park. You wouldn't want to hide the treasure in places that are hard to reach or that's blocked by tall trees, just like survey stations shouldn't be placed in difficult terrains that make it hard to see or access. Choosing the right spots makes the hunt (or survey) successful and efficient!
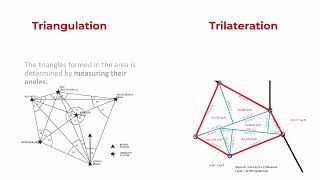
Triangulation and Trilateration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Trilateration is a surveying procedure in which the lengths of the sides of a triangle of the triangulation scheme are measured, generally electronically, and included angles are determined trigonometrically. While triangulation uses angles, trilateration relies solely on measuring side lengths.
Detailed Explanation
Trilateration differs from triangulation in that it focuses on direct distance measurements rather than calculating angles. This method is highly effective for determining positions, especially with modern Electronic Distance Measurement (EDM) technology, which has greatly increased the accuracy of such measurements. Each method has its applications, but they can complement each other in a comprehensive survey.
Examples & Analogies
Think of triangulation like using a protractor to measure the angles of a triangle on paper, while trilateration is like using a tape measure to find the exact lengths of the triangle's sides. Both methods can tell you about the triangle's shape, but they use different tools to do so.
Principles of Accuracy in Triangulation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In triangulation, the entire area to be surveyed is divided into a framework of triangles. Triangulation is more accurate than the theodolite transverse because there is less accumulation of error. A series of triangulation may consist of simple triangles, braced quadrilaterals, and centered polygons.
Detailed Explanation
Triangulation's framework structure minimizes errors across the survey area by distributing them more evenly. Simple triangles may accumulate errors because there is only one way to calculate distances, while braced quadrilaterals offer multiple ways to validate measurements, increasing overall accuracy. Centered polygons provide additional checks and better results, though they require more calculation time.
Examples & Analogies
Consider a group of friends spreading out to explore a park. If they only rely on one friend (like a simple triangle), they may not notice some paths. But if they work in pairs or groups (like a braced quadrilateral), they're more likely to cover more ground efficiently and accurately!
Types of Triangulation Schemes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The triangulation schemes are classified into three categories: (i) First order or Primary triangulation, (ii) Second order or Secondary triangulation, and (iii) Third order or Tertiary triangulation. The basis of the classification is the accuracy with which the length and azimuth of a line are determined.
Detailed Explanation
Each category of triangulation is distinguished by accuracy and application. Primary triangulation is the most accurate and is used for critical measurements, while secondary and tertiary triangulations are used for less critical measurements and finer details in smaller areas. This tiered approach allows surveyors to efficiently manage their resources and accuracy needs based on specific project requirements.
Examples & Analogies
Think of this classification like a grading system in school. Just as top students might be recognized for higher achievements (like primary triangulation), other students who perform well at different levels are also acknowledged (secondary and tertiary). This structured approach helps focus efforts where they are most needed.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Triangulation: A method of using triangles to compute positions based on known lengths and angles.
-
Control Points: Critical fixed points used to ensure measurement accuracy in surveying.
-
Trilateration vs. Triangulation: Understanding how the two methods differ based on what is measured.
-
Accuracy in Measurement: The importance of precision in the surveying process to avoid errors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating the angles of a triangle when the base is known in a triangulation survey.
-
Using triangulation to map out a new construction site by establishing control points.
-
Employing trilateration to determine the positions of GPS satellites for navigation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In triangulation, we set our sights, Control points shining in clear daylight.
📖 Fascinating Stories
-
Imagine a surveyor, with maps in hand, using triangles to trace out the land, control points as stars in the surveying sky.
🧠 Other Memory Gems
-
Remember 'TAC' for Triangles, Angles, and Control points in triangulation.
🎯 Super Acronyms
OPV for Optimal Points and Visibility when selecting triangulation stations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Triangulation
Definition:
A surveying method where distances and angles are utilized for locating points through the geometric properties of triangles.
-
Term: Control Point
Definition:
Fixed locations known as triangulation stations from which measurements are taken during surveying.
-
Term: Trilateration
Definition:
A surveying method focused on measuring the lengths of sides of triangles to calculate angles, contrasting with triangulation.
-
Term: Baseline
Definition:
The side of the triangle used as a reference for measuring angles in triangulation surveys.
-
Term: Visibility
Definition:
The ability to clearly see and measure triangulation stations without obstruction, often determined by terrain.
-
Term: Correction Factors
Definition:
Adjustments made to measurements to improve accuracy due to environmental factors.