Vertical Alignment
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vertical Alignment and Gradients
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we will explore the concept of vertical alignment in road design. Can someone tell me what vertical alignment refers to?

Is it about how roads are designed vertically? Like hills and slopes?

Exactly! It involves the gradients—how the road rises or falls. Can someone explain what a gradient is?

A gradient is like the slope of the road—how steep it is, right?

Correct! Gradients can greatly affect vehicle operation and road safety. Anyone remember the two types of vertical curves?

Summit curves and valley curves!

Great! Summit curves are convex. Why are they important?

They help in making the transition smooth between different gradients, right?

Exactly! Smooth transitions enhance driver comfort. Remember, the visual representation of these concepts is crucial!
Effects of Gradient on Vehicle Performance
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's talk about how gradients affect vehicle performance, especially heavy vehicles. Why do you think steep gradients are avoided?

Because they make it hard for vehicles to climb?

Correct! Steep gradients can slow down heavy vehicles, which also affects the speed of lighter vehicles. Can someone elaborate on the sight distance?

Sight distance is how far a driver can see, especially important on uphill grades?

Exactly! Poor sight distance can increase accident risks. Let's remember the example of steep gradients causing a reduction in overall road capacity!

So, balancing gradient design is crucial for safety and efficiency!

Absolutely! Always consider both safety and operational costs in gradient design.
Types of Gradients
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s explore the various types of gradients. Can anyone name them?

There are ruling, limiting, exceptional, and minimum gradients.

Correct! Let’s go through each one. What defines the ruling gradient?

It’s the max slope designers aim for, considering factors like terrain.

Very good! And what about limiting gradients?

They are used when costs for ruling gradients are too high!

Spot on! Exceptional gradients are used in very steep conditions for short stretches. And minimum gradients?

They’re important for drainage, ensuring water flows properly!

Exactly! Remember, each gradient type has its role in ensuring both functionality and safety.
Creeper Lanes and Grade Compensation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s dive into some special features like creeper lanes. What are they?

They help slow vehicles get out of the way of faster ones on steep inclines.

Correct! Their design depends on reducing speed effectively. Next, what is grade compensation?

Isn’t that reducing the gradient around horizontal curves to help with traction?

Exactly! This is vital to ensure vehicles don't lose traction on curves. Can anyone give examples of how grade compensation works?

If the curve has a steep gradient, the gradient needs compensation to ensure safer driving conditions!

Right! Proper design enhances safety significantly.
Designing Summit Curves
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let's discuss summit curves in detail. What makes them critical in road design?

They provide a smooth transition from one gradient to another.

Correct! And what about their shape? Why are parabolic curves commonly used?

Parabolic curves are easier to calculate and provide better comfort for drivers.

Great! Remember the importance of sight distance in these curves. What aids safe driving?

Adequate sight distance helps drivers see obstructions early.

Exactly! Summarizing, summit curves enhance safety and comfort for drivers.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section details the concepts of vertical alignment in road designs, including gradients, their effects on vehicular speed, different types of gradients, and the significance of summit curves in ensuring safe transitions between gradients.
Detailed
Detailed Summary
The vertical alignment of a roadway plays a crucial role in its overall design and safety. This section elaborates on gradients, which define the rise or fall of roads with respect to horizontal distances, represented graphically in a profile view. Vertical curves connect two different gradients and form either summit curves (convex) or valley curves (concave). Steep gradients are generally avoided due to increased construction costs and challenges for heavy vehicles. The effects of these gradients on the speed of vehicles, especially heavy ones, are significant, leading to changes in road capacity and accident risks.
Different types of gradients are defined: ruling gradients (design limits), limiting gradients (cost factors), exceptional gradients (steep conditions for short distances), and minimum gradients (for drainage). Special features like creeper lanes facilitate vehicle flow on steep inclines, allowing slower-moving vehicles to bypass faster ones. Furthermore, grade compensation is vital when gradients coincide with horizontal curves to reduce traction loss. The section concludes with a focus on summit curves, detailing their design, length considerations, and benefits regarding driver comfort and safety.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Vertical Alignment
Chapter 1 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The vertical alignment of a road consists of gradients (straight lines in a vertical plane) and vertical curves. The vertical alignment is usually drawn as a profile, which is a graph with elevation as the vertical axis and the horizontal distance along the center line of the road as the horizontal axis. Just as a circular curve is used to connect horizontal straight stretches of road, vertical curves connect two gradients. When these two curves meet, they form either convex or concave. The former is called a summit curve, while the latter is called a valley curve. This section covers a discussion on gradient and summit curves.
Detailed Explanation
Vertical alignment refers to how a road is structured in terms of its height and slope. This can include rising paths (gradients) and curved sections (vertical curves). The vertical alignment is essential for understanding how vehicles navigate the road. It is graphically represented as a profile chart, where the vertical line shows height (elevation) and the horizontal line shows distance along the road. When the straight paths on a vertical profile connect with slopes, they form different types of curves depending on their shape. A summit curve is formed by two rising gradients, while a valley curve connects two descending ones.
Examples & Analogies
Think of a roller coaster. The upward hills are like summit curves, where the coaster goes up, and the downward slopes are comparable to valley curves as it dips down. Just as a roller coaster's design affects how thrilling or comfortable the ride is, the vertical alignment of a road affects how smooth and safe the driving experience will be.
Understanding Gradient
Chapter 2 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Gradient is the rate of rise or fall along the length of the road with respect to the horizontal. While aligning a highway, the gradient is decided designing the vertical curve. Before finalizing the gradients, the construction cost, vehicular operation cost and the practical problems in the site also have to be considered. Usually steep gradients are avoided as far as possible because of the difficulty to climb and increase in the construction cost. More about gradients are discussed below.
Detailed Explanation
A gradient indicates how steep a road is, either going up or down. It is essential to consider the gradient when designing a highway, as it directly affects vehicle performance. If roads are too steep to drive on, they become impractical. Designers must weigh various factors, such as construction costs and how vehicles will perform on these slopes. Steeper grades can require more materials and labor to build and can make it hard for vehicles, especially bigger ones, to climb without difficulty.
Examples & Analogies
Imagine riding a bicycle up a hill. If the hill is not too steep, you can manage it easily. However, if the incline is steep, you may struggle to maintain your speed or even to ascend at all without getting off your bike. Road gradients work the same way: too steep, and vehicles may not be able to climb efficiently.
Effects of Gradient on Vehicles
Chapter 3 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The effect of long steep gradient on the vehicular speed is considerable. This is particularly important in roads where the proportion of heavy vehicles is significant. Due to restrictive sight distance at uphill gradients, the speed of traffic is often controlled by these heavy vehicles. As a result, not only the operating costs of the vehicles are increased, but also the capacity of the roads will have to be reduced. Further, due to high differential speed between heavy and light vehicles, and between uphill and downhill gradients, accidents abound in gradients.
Detailed Explanation
Steep gradients can significantly slow down vehicles, especially heavy ones. This slowing down can affect the overall traffic flow, making the road less efficient. When heavy vehicles struggle to climb hills, they tend to move slower, reducing the speed of other vehicles around them, leading to traffic jams. The differences in speed can also create dangerous situations, increasing the risk of accidents.
Examples & Analogies
Imagine a two-lane road where a slow-moving truck climbs a hill. Cars behind the truck are forced to slow down and may become frustrated. As they attempt to overtake the truck on a steep gradient, they risk not seeing incoming traffic due to limited sight distance, much like trying to pass another vehicle at the top of a hill without knowing if there's another car coming the other way.
Gradient Representation
Chapter 4 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The positive gradient or the ascending gradient is denoted as +n and the negative gradient as -n. The deviation angle N is: when two grades meet, the angle which measures the change of direction and is given by the algebraic difference between the two grades (n1 - n2) = n1 + n2 = α + α. Example: 1 in 30 = 3.33% is a steep gradient, while 1 in 50 = 2% is a flatter gradient.
Detailed Explanation
Gradient values are often presented in mathematical terms, indicating how steeply a road rises or falls. A positive gradient (+n) shows an uphill slope, while a negative gradient (-n) represents a downhill slope. The deviation angle is crucial for engineering, as it helps determine how the direction and steepness of road grades interact when they meet at a junction. This representation allows engineers to communicate effectively about road designs.
Examples & Analogies
When hiking, if you see a sign that says '1 in 30', it means that for every 30 units you travel horizontally, there is a rise of 1 unit. This can help you understand how steep the path will be, allowing you to prepare for the effort required to traverse it.
Types of Gradient
Chapter 5 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Many studies have shown that gradient up to seven percent can have considerable effect on the speeds of the passenger cars. On the contrary, the speeds of the heavy vehicles are considerably reduced when long gradients as flat as two percent are adopted. Although flatter gradients are desirable, it is evident that the cost of construction will also be very high. Therefore, IRC has specified the desirable gradients for each terrain.
Detailed Explanation
Different kinds of gradients exist based on how steep or flat they are, and each type has a significant impact on vehicle speeds. For example, gradients of up to 7% can slow cars but affect heavier vehicles to an even greater extent at flatter gradients of around 2%. While flatter gradients may make driving easier, they come with higher construction costs, which needs to be carefully managed by road planners.
Examples & Analogies
Think of a moving sidewalk at an airport. If it's very steep, it can only support lighter luggage carts moving up and down at a more difficult pace. If it's flat, it can support multiple carts moving smoothly side-by-side but would require more space and resources to build effectively.
Ruling Gradient
Chapter 6 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The ruling gradient or the design gradient is the maximum gradient with which the designer attempts to design the vertical profile of the road. This depends on the terrain, length of the grade, speed, pulling power of the vehicle, and the presence of the horizontal curve. In flatter terrain, it may be possible to provide flat gradients, but in hilly terrain it is not economical and sometimes not possible at all.
Detailed Explanation
The ruling gradient is the target steepness set by engineers when designing a road. This gradient takes into account various factors including the type of terrain and the vehicle types expected to use the road. Designers aim to avoid steep gradients where possible because they complicate vehicle movement and increase construction costs.
Examples & Analogies
When designing a walking path up a hill, a ruling gradient might be like trying to make the slope gentle so that more people can walk up without getting exhausted, just like a builder targets reasonable car speeds while ensuring safety.
Limiting Gradient and Exceptional Gradient
Chapter 7 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This gradient is adopted when the ruling gradient results in enormous increase in cost of construction. On rolling terrain and hilly terrain, it may be frequently necessary to adopt limiting gradients. Exceptional gradients are very steeper gradients given at unavoidable situations. They should be limited for short stretches not exceeding about 100 meters at a stretch.
Detailed Explanation
Limiting gradients are used when sticking to the ruling gradient would make road construction too expensive or impractical. Exceptional gradients are allowed in extreme circumstances, usually only for short distances. Both of these types of gradients are critical for ensuring that roads are functional despite varying geographical challenges.
Examples & Analogies
Consider a convenience store on the side of a steep hill. The builder may need to make the sidewalk steep for a short distance because the road itself is already too cramped for a gentle slope. This avoids excessive costs while still providing access.
Minimum Gradient
Chapter 8 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Minimum gradient is important only at locations where surface drainage is important. Camber will take care of the lateral drainage, but the longitudinal drainage along the side drains requires some slope for smooth flow of water. Therefore minimum gradient is provided for drainage purposes directly tied to rainfall, soil type, and other site conditions.
Detailed Explanation
Minimum gradient ensures that water flows off the road surface efficiently, which is especially important in preventing flooding and maintaining road integrity. Instead of allowing water to pool, a minimum gradient, sometimes as slight as 1 in 500, ensures that drainage systems work properly, which is crucial for road safety and longevity.
Examples & Analogies
Think of a garden where water needs to drain away after it rains. If the garden is flat, puddles form. By ensuring a slight slope, rainwater can flow away efficiently, just like roads need to be designed to guide water away to prevent damage or hazardous driving conditions.
Creeper Lane
Chapter 9 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When the uphill climb is extremely long, it may be desirable to introduce an additional lane so as to allow slow ascending vehicles to be removed from the main stream so that fast-moving vehicles are not affected. Such a newly introduced lane is called creeper lane.
Detailed Explanation
Creeper lanes are added to lengthy uphill stretches to allow slower vehicles, often trucks, to avoid holding up faster traffic. This helps maintain a steady flow of vehicles as those who struggle on hills can use this lane while others continue to travel without delays.
Examples & Analogies
Picture a multi-lane highway with a steep incline. If a truck moves slowly, it can block several cars behind it trying to speed up. A creeper lane on the side lets the truck drive at its own pace while faster cars use the main lanes to maintain their speed, similar to how people at a cafe may allow slower eaters to slide over to a different table so that faster diners can enjoy their meal uninterrupted.
Grade Compensation
Chapter 10 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
While a vehicle is negotiating a horizontal curve, if there is a gradient also, then there will be increased resistance to traction due to both curve and the gradient. In such cases, the total resistance should not exceed the resistance due to the gradient specified.
Detailed Explanation
Grade compensation is used to adjust gradients on roads with curves. When vehicles travel around a curve while also climbing or descending, they face extra resistance. It's essential to ensure that the combined resistance from the curve and the slope does not exceed what vehicles can handle. Proper compensation allows for smoother driving and reduces risks of accidents due to uncontrolled speeds.
Examples & Analogies
Imagine going around a turn on a bicycle while riding uphill. The effort to pedal increases both because of the uphill slope and the tight turn. Grade compensation would be like adjusting the slope so it’s a bit gentler through the turn, making it easier to ride without exhausting yourself.
Summit Curves
Chapter 11 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Summit curves are vertical curves with gradient upwards. They are formed when two gradients meet. Many curve forms can be used with satisfactory results, with parabolic curves being preferred for their ease of layout and comfort during transitions.
Detailed Explanation
Summit curves are designed to allow for smooth transitions when changing gradients from uphill to either flat or downhill. The shape of these curves significantly impacts how comfortable and safe the driving experience is. Engineers often prefer parabolic shapes because they are easy to design and provide good riding comfort.
Examples & Analogies
When walking up and over a hill, a gradual slope (like a parabolic curve) feels much easier than a steep rise followed by a sharp drop. Just as you would want hills on a walking path to be smooth for comfort, roads benefit from summit curves to keep driving comfortable and safe.
Design Considerations for Summit Curves
Chapter 12 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In determining the type and length of the vertical curve, the design considerations are comfort and security of the driver, and the appearance of the profile alignment. Among these, sight distance requirements for safety is most important on summit curves.
Detailed Explanation
When designing summit curves, factors like driver comfort and safety are critical. Adequate sight distance must be available to ensure drivers can react to potential obstructions ahead. This requires careful planning to ensure that the length of curves accommodates a safe stopping distance so that drivers can safely navigate around any obstacles.
Examples & Analogies
Think about driving on a winding mountain road. If a turn is too sharp and you can't see around it, you risk an accident. Designers of these roads must consider how far ahead drivers need to see to safely make turns, similar to how a cyclist anticipates a bend to avoid losing control.
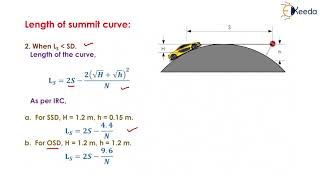
Length of Summit Curve
Chapter 13 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The important design aspect of the summit curve is the determination of the length of the curve which is parabolic. As noted earlier, the length of the curve is guided by the sight distance consideration.
Detailed Explanation
Determining the length of summit curves is crucial. The longer the curve, the more drivers can see ahead and prepare for changes in the road. Designers will calculate the ideal length based on sight distances, ensuring that if there is something blocking the road, drivers have ample time to stop safely.
Examples & Analogies
When setting up a safety barrier at an amusement park ride, the designers consider how far away observers are allowed to stand to see the ride properly. Similarly, engineers make sure that road curves allow adequate sight distances so drivers have a clear view for safe driving, just like the safety barrier keeps spectators at a safe distance.
Summary
Chapter 14 of 14
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Different types of gradients and IRC recommendations for their maximum and minimum limit were discussed. At points of combination of horizontal curve and gradient, grade compensation has to be provided.
Detailed Explanation
The chapter emphasizes various gradient types and how they influence road design, including standards set by the IRC for safe engineering practices. Roads must be designed considering horizontal curves and gradients simultaneously, which may require grade compensation to ensure safe vehicle operation.
Examples & Analogies
When baking a cake, if you put too much batter in one side and not in the other, it may tilt as it cooks. Engineers must balance road design just as bakers balance ingredients to avoid problems and ensure safety while driving.
Key Concepts
-
Vertical Alignment: The arrangement of vertical elements in road design to ensure safe and efficient traffic flow.
-
Gradients: The slopes of the road that impact vehicle performance and safety.
-
Summit Curves: Crucial for changing gradients smoothly, enhancing driver comfort.
-
Creeper Lanes: Essential for managing slow vehicle movement on steep inclines.
-
Grade Compensation: Important adjustment made at horizontal curves to maintain safety.
Examples & Applications
A steep road with a gradient of 8% may cause heavy vehicles to slow down significantly, affecting traffic flow.
In mountainous areas, summit curves help drivers maintain speed and comfort while transitioning between different road elevations.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When roads incline, smooth curves we find, driver comfort designed with safety in mind.
Stories
Imagine a mountain road where vehicles climb slowly; summit curves help them glide smoothly over hills, avoiding sharp drops.
Memory Tools
Remember 'GRS' for gradients: 'G' for Gradient, 'R' for Ruling, 'S' for Summit Curves.
Acronyms
Use 'GEM' to recall layout
'G' for Gradients
'E' for Effects on movement
'M' for Minimum Gradient.
Flash Cards
Glossary
- Vertical Alignment
The vertical shaping of a roadway consisting of gradients and curves.
- Gradient
The rate of rise or fall along the road's length with respect to horizontal distance.
- Summit Curve
A convex vertical curve connecting two gradients, allowing a smooth transition.
- Valley Curve
A concave curve joining two gradients, usually at the bottom of a dip.
- Creeper Lane
An additional lane on steep gradients for slow-moving vehicles.
- Grade Compensation
The adjustment of gradient at horizontal curves to maintain tractive force.
- Ruling Gradient
The maximum gradient that should ideally be designed for.
- Limiting Gradient
The gradient adopted when the ruling gradient becomes economically unviable.
- Exceptional Gradient
Very steep gradients used in unavoidable situations for short distances.
- Minimum Gradient
The least slope required for effective drainage.
Reference links
Supplementary resources to enhance your learning experience.
