Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Defining a Functional Interface
Unlock Audio Lesson
Today we're going to define a custom functional interface. Who can tell me what a functional interface is?
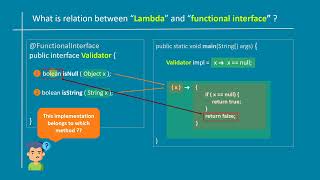
Is it an interface with just one abstract method?
Exactly! We will create one called `MathOperation` that will have a method `operate(int a, int b)`. Does anyone know why we would want to create such an interface?
So we can use lambda expressions to provide different implementations?
Yes! That's the beauty of it. Let's define our interface. Remember, it must be annotated with `@FunctionalInterface` to indicate its purpose.
What does that annotation do?
It ensures that the interface adheres to the single abstract method rule and helps avoid mistakes.
Let's summarize what we've done: we defined a functional interface called `MathOperation`.
Implementing Lambda Expressions
Unlock Audio Lesson
Now that we've defined our functional interface, let's implement it using lambda expressions. What operations might we define with `MathOperation`?
Addition and multiplication!
Great! Let's write lambda expressions for both. For addition, we can use `addition = (a, b) -> a + b;`. What do you think this means?
It defines what the `operate` method does when we call it with two numbers!
Exactly! Now, what about multiplication?
That would be `multiply = (a, b) -> a * b;`.
Perfect! So we have both operations defined. To recap, we've used lambda expressions to implement our `MathOperation` interface for addition and multiplication.
Using the MathOperation Interface
Unlock Audio Lesson
Now, let's take it a step further. How would you use the `MathOperation` interface in a Java program?
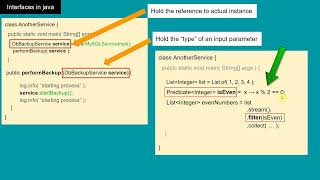
We have to create instances of the interface and call the `operate` method?
Exactly! You can use `System.out.println` to display the results. Can anyone write a line of code to show the result of adding two numbers?
Sure! It would be `System.out.println("Addition: " + addition.operate(5, 3));`.
Well done! This line will output the result of the addition. Remember to implement both operations in your `main` method.
Let's summarize what we've covered: we implemented a functional interface and used lambda expressions to define operations. We also looked at how to use these operations in our main program.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, a custom functional interface named 'MathOperation' is defined, along with two lambda expressions for addition and multiplication. This demonstrates how lambda expressions can be used to implement the interface succinctly.
Detailed
Custom Functional Interface Example
In this section, we explore a practical implementation of a custom functional interface in Java. A functional interface is characterized by having a single abstract method, which can be implemented using lambda expressions for conciseness and clarity.
Definition of Custom Functional Interface
We define a functional interface named MathOperation with an abstract method operate(int a, int b). This interface will allow us to perform mathematical operations:
Lambda Expressions Implementation
In the main class LambdaExample, we create two lambda expressions: one for addition and another for multiplication. Each implementation corresponds to the operate method defined in MathOperation:
Significance
This example encapsulates the core benefits of using functional interfaces and lambda expressions in Java: reducing boilerplate code and enhancing readability. The ability to define operations using lambda expressions simplifies the coding process and refines the overall structure of Java applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Custom Functional Interfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
@FunctionalInterface
interface MathOperation {
int operate(int a, int b);
}
Detailed Explanation
In Java, a functional interface is an interface that contains exactly one abstract method. This example defines a custom functional interface named MathOperation. By using the @FunctionalInterface annotation, we indicate that this interface is intended to be used with lambda expressions or method references. The method operate(int a, int b) allows subclasses or lambda expressions to implement the behavior of mathematical operations, which, in this case, will require two integer parameters.
Examples & Analogies
Imagine you have a single button that performs different mathematical operations based on how it is used. A MathOperation interface acts like that button—it accepts different lambda expressions as behaviors but only allows one method to execute at a time.
Lambda Expressions Implementing MathOperation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
public class LambdaExample {
public static void main(String[] args) {
MathOperation addition = (a, b) -> a + b;
MathOperation multiply = (a, b) -> a * b;
System.out.println("Addition: " + addition.operate(5, 3));
System.out.println("Multiplication: " + multiply.operate(5, 3));
}
}
Detailed Explanation
In the main method of the LambdaExample class, two instances of the MathOperation interface are created using lambda expressions. The first instance addition defines a lambda that takes two integers and returns their sum. The second instance multiply takes two integers and returns their product. The results of both operations are printed to the console by calling the operate method on each instance with the integers 5 and 3.
Examples & Analogies
Consider a restaurant where chefs can create different dishes based on the same ingredients. Here, the ingredients are the integers (5 and 3), and the dishes are the operations: addition or multiplication. Each chef (lambda expression) takes the same ingredients and creates different outcomes, just like the addition and multiply operations produce different results using the same numbers.
Output of the Example
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
System.out.println("Addition: " + addition.operate(5, 3));
System.out.println("Multiplication: " + multiply.operate(5, 3));
Detailed Explanation
The two System.out.println statements display the results of the operations on the integers 5 and 3. The first line outputs the result of the addition operation, while the second one outputs the result of the multiplication operation. Based on the lambda expressions defined earlier, the output will be: 'Addition: 8' for the addition and 'Multiplication: 15' for the multiplication.
Examples & Analogies
If you think of a simple calculator, each operation yields a different result. In this scenario, the calculator performs two operations: one addition and one multiplication. When you input 5 and 3, the calculator shows you 8 for addition and 15 for multiplication, illustrating how different operations can yield distinct results from the same inputs.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Functional Interface: An interface with one abstract method that can be implemented with lambdas.
-
Lambda Expression: A concise way to express a function that can be passed as an argument.
-
Anonymous Function: A function defined without a name, often used with lambda expressions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Define a functional interface: @FunctionalInterface interface MathOperation { int operate(int a, int b); }
-
Implement addition and multiplication using lambda: MathOperation addition = (a, b) -> a + b; MathOperation multiply = (a, b) -> a * b;
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If it's just one method, here's what you should try,
📖 Fascinating Stories
-
Once upon a time, there was a Math wizard who created spells for addition and multiplication using a magical formula called 'lambda'. The wizard made math simple and fun!
🧠 Other Memory Gems
-
Remember 'MALM' for Math-Actions via Lambda Method: MathOperation, Addition, Lambda, Multiplication.
🎯 Super Acronyms
LAM for Lambda
- L: stands for 'Lambda'
- A: stands for 'Abstract method'
- M: stands for 'Magic of interfaces'.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Functional Interface
Definition:
An interface that has exactly one abstract method and can be implemented using lambda expressions.
-
Term: Lambda Expression
Definition:
An anonymous function that can be passed as an argument or assigned to a variable, providing an implementation for a functional interface.
-
Term: MathOperation
Definition:
A custom functional interface defined for performing mathematical operations with a single method 'operate'.