Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Functional Programming
Unlock Audio Lesson
Welcome back, class! Today, we're diving into functional programming. So, what do you think functional programming is?
Is it about using functions more than other constructs?
Exactly! Functional programming treats computation as the evaluation of mathematical functions, emphasizing immutability and statelessness. Who can tell me what a first-class function is?
I think first-class functions are functions that can be treated like any other variable, right?
Precisely! They can be passed as arguments or returned from other functions. Great job!
Core Principles of Functional Programming
Unlock Audio Lesson
Now, let’s discuss pure functions. Can anyone explain what this means?
A pure function always gives the same output for the same input, right? It doesn’t depend on or change any external state?
Correct! This predictability makes them easier to debug and test. Now, what are higher-order functions?
Aren't they functions that take other functions as parameters or return them?
Excellent! This is key in functional programming, allowing us to create more abstract and reusable code.
Benefits of Functional Programming
Unlock Audio Lesson
What do you all think are some benefits of functional programming?
It sounds like it can make code easier to understand because of its predictable behavior.
And if they're pure, they can be tested easily! Less side effects mean higher reliability.
Great observations! Additionally, functional programming supports parallelism due to its statelessness, allowing for better utilization of resources.
I see how that can help with performance in large applications!
Recursion in Functional Programming
Unlock Audio Lesson
Let’s now consider recursion. Does anyone know how recursion differs from traditional looping?
Instead of using loops, a recursion calls itself until it reaches a base case, right?
Exactly! This is often used in functional programming to solve problems. Who can give an example of an application of recursion?
Calculating factorials could be one example!
Great example! Factorials illustrate how recursion can replace loops and simplify certain tasks.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Functional programming treats computation as the evaluation of mathematical functions and emphasizes immutability and statelessness, highlighting core principles like first-class, pure, and higher-order functions, alongside benefits like predictable behavior and ease of testing.
Detailed
Functional Programming Concepts
Functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions. This section delves into core concepts that define functional programming and explains its advantages in creating software that is predictable, maintainable, and easier to test and debug.
Definition
Functional programming is fundamentally grounded in the mathematical concept of functions, where programs are constructed as a series of function evaluations rather than as a sequence of commands.
Core Concepts
- First-class functions: Functions are treated as first-class citizens; they can be assigned to variables, passed as arguments, or returned from other functions.
- Pure functions: Functions that always produce the same output for the same input and do not cause side effects, making them predictable and easy to debug.
- Higher-order functions: Functions that can take other functions as arguments and/or return them as results, enabling more abstract and powerful programming styles.
- Lambda expressions: Anonymous functions that can be defined in a concise manner, allowing for functional-style treatment of code.
- Recursion: A method where a function calls itself to solve a problem, often used in functional programming in place of traditional looping constructs.
Benefits
Functional programming offers several compelling benefits:
- Predictable behavior: The absence of side effects leads to more predictable and reliable code.
- Easy to test and debug: Pure functions reduce the complexity of testing, as they do not depend on external state.
- Supports parallelism: Functional programming naturally lends itself to parallel execution, leveraging its stateless nature.
In summary, understanding functional programming concepts is crucial for developers looking to enhance the efficiency and maintainability of their software.
Youtube Videos
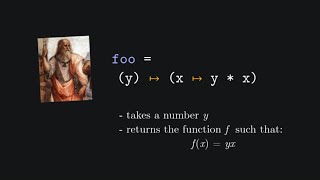
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Functional Programming
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Treats computation as the evaluation of mathematical functions.
• Emphasizes immutability and statelessness.
Detailed Explanation
Functional programming is a programming paradigm that views computation as the evaluation of mathematical functions. This means that instead of focusing on how to execute a sequence of commands, it emphasizes the outcomes of functions based on their inputs. In this context, immutability refers to the idea that once a variable is created, its state cannot be changed. Statelessness indicates that functions don't rely on internal state or outside data, making them predictable and easy to understand.
Examples & Analogies
Think of a vending machine. You put in money (input) and select a snack (function). The machine doesn't change its state or remember your previous choices; it simply gives you the snack you asked for, based on the money you put in. Each time you interact with it, it gives you a clear outcome without carrying over any previous information.
Core Concepts of Functional Programming
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• First-class functions.
• Pure functions.
• Higher-order functions.
• Lambda expressions.
• Recursion.
Detailed Explanation
Functional programming has several core concepts. First-class functions refer to the ability for functions to be treated as values, meaning they can be assigned to variables, passed as arguments, and returned from other functions. Pure functions are those that produce the same output given the same input and do not cause side effects, which helps in maintaining predictable behavior. Higher-order functions are functions that can take other functions as arguments or return them, enabling powerful abstractions. Lambda expressions offer a concise way to define anonymous functions. Lastly, recursion is a technique where a function calls itself in order to solve a problem, commonly used in functional programming since it allows for elegant solutions to complex problems.
Examples & Analogies
Imagine you are at a restaurant. The chef (function) can prepare any dish (output) as long as you provide the right ingredients (inputs). A first-class function is like a dish that you can substitute with another one (letting you choose how you want it prepared). A pure function is like a recipe that always yields the same dish if you follow it correctly, regardless of who follows it. A higher-order function is akin to the chef being able to create new recipes based on existing ones. Lambda expressions are like shorthand notes for quick recipes, and recursion could be likened to someone asking the chef to keep making a dish until they’re satisfied with it.
Benefits of Functional Programming
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Predictable behavior.
• Easy to test and debug.
• Supports parallelism.
Detailed Explanation
Functional programming comes with several benefits that make it a valuable paradigm for developers. Predictable behavior is a key advantage because pure functions do not depend on any hidden state, making it straightforward to understand how functions will behave based on their inputs. This predictability simplifies both testing and debugging processes since a function's output can always be traced back to its inputs without worrying about complicated state changes. Additionally, functional programming is conducive to parallelism, which allows multiple functions to be executed simultaneously without interference, thus increasing efficiency and performance in programs.
Examples & Analogies
Consider a library where each book can be borrowed independently of others. This is like functional programming where every function operates based solely on its inputs (the book's content). The librarian represents predictable behavior, keeping track of which books are being borrowed. Testing any particular book (or function) is straightforward as you can easily return it to the shelf without affecting others. Now, if you have lots of people wanting to borrow books at the same time, the library can handle it smoothly since each transaction is independent, similar to how functions in a functional programming setup can run in parallel.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
First-class functions: Functions that can be treated like any other variable in the program.
-
Pure functions: Reliable functions that yield the same result for identical inputs without side effects.
-
Higher-order functions: Functions that can take other functions as inputs or return them as outputs.
-
Lambda expressions: A syntax for defining anonymous functions in a concise manner.
-
Recursion: A programming technique where a function calls itself to solve problems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of a first-class function is when you store a function in a variable and then call it:
let add = function(x, y) { return x + y; };. -
A pure function example is the function
function square(x) { return x * x; }which does not modify any external state and only depends on its input.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In functional code, don't you fret, a pure function's a safe bet!
📖 Fascinating Stories
-
In a land of programmers, there lived a wise function named 'Pure.' Pure never changed; he only returned values. All the other functions followed him, realizing they could be equally reliable!
🧠 Other Memory Gems
-
Remember 'P-H-L-R' for Functional Programming: Pure, Higher-order, Lambda, Recursion.
🎯 Super Acronyms
FLIP - Functional programs
- Lambda
- Immutability
- Predictability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Firstclass function
Definition:
A function that can be treated like any other variable, able to be assigned, passed, or returned.
-
Term: Pure function
Definition:
A function that always produces the same output for the same input and does not cause side effects.
-
Term: Higherorder function
Definition:
A function that takes other functions as arguments and/or returns a function.
-
Term: Lambda expression
Definition:
An anonymous function expressed as a concise, inline function.
-
Term: Recursion
Definition:
A technique where a function calls itself to solve a problem.