Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Spectral Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're starting with spectral analysis, which is crucial for breaking down signals into their frequency components. Can anyone tell me the purposes of spectral analysis?
It helps to identify dominant frequencies and noise in signals?
Exactly! And itβs used in many fields. One way to remember that is the acronym **CAN** for Communications, Audio, and Neuroscience. So, what about the difference between time and frequency domains?
The time domain shows how a signal changes over time, while the frequency domain breaks it down into its sinusoidal components.
Well put! The time domain is mainly for seeing amplitude and shape, whereas the frequency domain helps with periodic structures and filtering behavior.
So when dealing with signals, we need to analyze them in both domains to get the full picture?
Absolutely! Letβs recap: spectral analysis identifies frequencies and is vital in many applications, and understanding time vs. frequency domains is key to effective signal analysis.
Fourier Transform Basics
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, letβs focus on the Fourier Transform. Who can explain what it does?
It converts a time-domain signal into its frequency-domain representation.
Correct! The formula we use is quite powerful: X(f) = β«βββ x(t) e^(-j2Οft) dt. This indicates the frequency content present in the signal. But how does this relate to digital signals?
For digital signals, we use the Discrete Fourier Transform (DFT) because it maps discrete entries into frequency components.
Exactly! The DFT is a sampled version of the FT. However, it has its complexitiesβwhat's the main limitation?
The computation complexity of O(NΒ²) makes it slow for large datasets.
Right! These complexities bring us to the Fast Fourier Transform, which makes these calculations efficient. Let's summarize: the Fourier Transform provides insights into frequency content, transitioning us smoothly to the DFT.
Fast Fourier Transform (FFT)
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, onto the Fast Fourier Transform (FFT). Whatβs the primary advantage of using the FFT?
It reduces the complexity from O(NΒ²) to O(N log N), allowing for real-time processing.
Exactly! The FFT enables efficient signal processingβhow does it achieve this?
It breaks the signal into smaller parts recursively and combines the results.
Great insight! It uses properties of symmetry and periodicity of complex exponentials to do this. Can anyone name popular FFT algorithms?
Cooley-Tukey is the most common one, right?
Yes! Plus Radix-2 and Radix-4 algorithms based on signal length. Letβs recap today's session: the FFT is a powerful and efficient algorithm critical in various applications, especially in communications.
Applications and Limitations of FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, let's explore applications of the FFT. What fields use it?
Itβs used in modulation and demodulation in communication systems.
Correct! FFT helps with channel analysis and noise detection as well. Can anyone think of other applications?
Audio and image compression, like MP3 and JPEG?
Exactly! However, what limitations should we be mindful of when using the FFT?
The signal length should be a power of 2 for optimal performance, and we can face issues with spectral leakage.
Excellent points! And remember, respecting the Nyquist theorem is vital when sampling. Todayβs key takeaway is that while FFT is efficient and versatile, understanding its limitations is equally important.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section covers spectral analysis's role in identifying frequency components of signals, the differences between time and frequency domains, and the fundamentals of the Fourier Transform. It introduces the Fast Fourier Transform (FFT) as an efficient algorithm for computing the Discrete Fourier Transform (DFT) and discusses its advantages and applications, especially in communication systems.
Detailed
Detailed Summary
In this section, we delve deep into the concept of spectral analysis and its vital role in signal processing. Spectral analysis breaks down a signal to discern its frequency components, allowing for the identification of dominant frequencies, noise, and harmonics within various applications, such as communications, audio processing, and biomedical signals.
Time Domain vs. Frequency Domain
Understanding the difference between the time domain and frequency domain is crucial. The time domain represents a signal as it changes over time using tools like oscilloscopes and analog-to-digital converters (ADCs), ideal for assessing amplitude and shape. Conversely, the frequency domain articulates a signal in terms of its sinusoidal componentsβanalyzing periodicity and bandwidth using tools such as Fourier Transform and Spectrum Analyzers.
Fourier Transform Basics
The Fourier Transform (FT) converts a time-domain signal to its frequency-domain representation, providing insights into the amount of each frequency present within the signal, primarily applicable for continuous signals.
Discrete Fourier Transform (DFT)
In digital processing, we rely on the Discrete Fourier Transform (DFT). It maps finite, discrete signals into frequency components. The DFT, however, has a computational complexity of O(NΒ²), which can be prohibitive for larger datasets.
Fast Fourier Transform (FFT)
The Fast Fourier Transform (FFT) revolutionizes this process by significantly lowering the complexity to O(N log N), thus enabling real-time analysis of large signals. Its mechanism involves breaking the signal into smaller parts recursively, leveraging the symmetry and periodicity of complex exponentials, applying algorithms like Cooley-Tukey, Radix-2, and Radix-4.
Applications of FFT in Communication Systems
Specifically in communication systems, the FFT plays a role in modulation and demodulation, channel analysis, noise detection, spectrum sensing, and even audio/image compression.
Advantages and Limitations
Despite its benefitsβsuch as speed, accuracy, versatility, and support for real-time processingβcertain limitations exist. These include the requirement that signal length must be a power of 2, potential spectral leakage due to non-periodic signals, and the constraints posed by the sampling rate as per Nyquistβs theorem.
In summary, mastering the FFT is essential for effectively implementing digital communication and DSP systems, providing insights into frequency content and aiding in various applications across engineering fields.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Spectral Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Spectral analysis involves decomposing a signal into its frequency components.
It helps identify dominant frequencies, noise, and harmonic content in signals.
Used in communications, audio processing, radar, biomedical signals, etc.
Detailed Explanation
Spectral analysis is a method used to break down a complex signal into its individual frequency components. This is important because different signals can be made up of many overlapping frequencies, and by identifying these components, we can better understand the signal's characteristics. For instance, in communications, spectral analysis can help engineers find out which frequencies are being used by different transmissions and whether there is unwanted noise present. This technique is not only useful in telecommunications but also in audio processing (like analyzing music), radar systems (like for tracking objects), and even in medicine for examining biomedical signals.
Examples & Analogies
Think of spectral analysis like tuning a musical instrument. When you play a note on a guitar, youβre not just hearing a single sound frequency but a combination of multiple frequencies that create the tone. Musicians or sound engineers might use spectral analysis tools to isolate these frequencies, to find out what needs to be adjusted to ensure the instrument sounds perfect.
Time Domain vs. Frequency Domain
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Domain Description Tools Used
Time Domain Signal is represented as it varies over Oscilloscopes, ADCs
Frequency Signal is represented in terms of Fourier Transform, Spectrum Analyzers
Time domain is useful for amplitude/shape; frequency domain shows periodic structure, bandwidth, and filtering behavior.
Detailed Explanation
The time domain and frequency domain are two different ways to represent signals. In the time domain, we observe how the signal changes over time: for instance, a waveform could show how the voltage varies as sound is played. Tools like oscilloscopes help visualize this. In contrast, the frequency domain represents the signal in terms of its frequency components; this is where we see how much of each frequency is present in the signal. This representation is particularly useful for understanding periodic patterns and filtering capabilities. Tools such as spectrum analyzers are used to analyze frequencies.
Examples & Analogies
Imagine youβre at a party where different music genres are being played. In the time domain, itβs like listening to the music as it plays, capturing how it changes with beats and pauses. But in the frequency domain, imagine analyzing the music to find out how many bass, treble, and mid-range sounds are there, and adjusting them for a better sound experience.
Fourier Transform (FT) Basics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fourier Transform (FT) converts a time-domain signal into its frequency-domain representation.
X(f) = β«βββx(t)eβj2Οftdt
It tells how much of each frequency is present in a signal.
Commonly used for continuous and infinite signals.
Detailed Explanation
The Fourier Transform (FT) is a mathematical tool that transforms a signal from the time domain into the frequency domain. This transformation allows us to see which frequencies exist in a given signal and in what proportions. The provided equation shows how the transform is computed, integrating over all time to reveal the frequency content of the signal. This concept is particularly relevant for continuous signals, which can have an infinite duration.
Examples & Analogies
Consider the Fourier Transform like a color filter that dissects light. When light passes through a prism, it spreads into various colors, much like how the FT reveals different frequency components within a signal by breaking it down into simpler elements.
Discrete Fourier Transform (DFT)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For digital signal processing, signals are discrete and finite.
DFT is the sampled version of FT:
X[k] = Ξ£n=0Nβ1 x[n] eβj(2Ο/N)kn,
k = 0, 1, ..., Nβ1
It maps N time samples into N frequency components.
Limitations:
High computational complexity: O(NΒ²)
Detailed Explanation
The Discrete Fourier Transform (DFT) is a specific case of the Fourier Transform applied to discrete and finite signal samples. Rather than processing an infinite signal, DFT processes a set number of samples, converting them into an equal number of frequency components. However, one of its main downsides is that the computational complexity can be quite high, resulting in performance challenges as the number of samples increases β specifically, O(NΒ²), where N represents the number of samples.
Examples & Analogies
Think of the DFT like a translator turning a page of text into another language. Each sentence (or time sample) is converted into corresponding phrases in the target language (frequency components). However, translating more pages (more samples) becomes more time-consuming and labor-intensive the more there are.
Fast Fourier Transform (FFT)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
FFT is an efficient algorithm to compute the DFT.
Reduces complexity from O(NΒ²) to O(N log N)
Enables real-time spectral analysis of large signals.
Popular FFT Algorithms:
β’ Cooley-Tukey FFT (most common)
β’ Radix-2, Radix-4 algorithms (based on signal length)
Detailed Explanation
The Fast Fourier Transform (FFT) is a highly efficient algorithm that computes the DFT more quickly by significantly lowering the computational complexity from O(NΒ²) to O(N log N). This efficiency makes it feasible to analyze large data sets in real time, which is crucial in many modern applications. There are various FFT algorithms available, with Cooley-Tukey being the most widely used, as well as specialized forms like Radix-2 and Radix-4 depending on the specific characteristics of the signal.
Examples & Analogies
Imagine having a large group of students to sort by height. A naive approach might be to compare each student with every other student, taking lots of time. However, if you use a clever strategy to divide the students into smaller groups first and sort those before merging them back together, you can do it much faster. The FFT adopts a similar strategy by breaking down the data into manageable parts to compute the results efficiently.
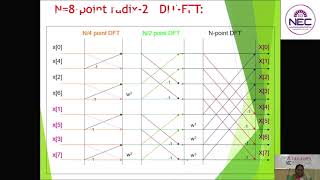
Working of FFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Breaks signal into smaller parts recursively.
Uses symmetry and periodicity properties of complex exponentials.
Combines results to compute full transform efficiently.
Input Requirement:
Number of samples N must be a power of 2 (for Radix-2 FFT).
Detailed Explanation
The working mechanism of the FFT involves recursively breaking the input signal into smaller segments, exploiting the properties of symmetry and periodicity in complex exponentials to simplify calculations. As each smaller segment is transformed, the results are combined to form the full FFT efficiently. However, for certain FFT algorithms like the Radix-2 FFT, the number of input samples must be a power of 2, which is an important consideration for implementation.
Examples & Analogies
Visualize solving a puzzle. Instead of trying to arrange all pieces at once, you first sort them into edge pieces, corner pieces, and similar colors. Each group is easier to handle, and combining the sorted sections at the end leads to a complete picture faster. The FFT structurally works in a similar way, focusing on smaller parts to expedite the process.
Applications of FFT in Communication Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β’ Modulation/Demodulation: Helps analyze frequency shift keying (FSK), OFDM systems.
β’ Channel Analysis: Identifying channel bandwidth and response.
β’ Noise Detection: Spotting unwanted frequencies in a spectrum.
β’ Spectrum Sensing: In cognitive radio, radar systems.
β’ Audio & Image Compression: Used in MP3, JPEG, and MPEG formats.
Detailed Explanation
FFT has a wide range of applications, particularly in communication systems. It is essential for modulation and demodulation processes, where it helps analyze how data is transmitted over different frequencies. In channel analysis, FFT enables the determination of bandwidth and system response to inform transmission settings. It also plays a vital role in noise detection by identifying unwanted frequencies and is crucial in spectrum sensing for necessary technologies like cognitive radios. Moreover, FFT assists in compressing audio and images, forming the basis for formats like MP3, JPEG, and MPEG.
Examples & Analogies
Think of FFT in the context of telecommunications like a conductor leading an orchestra. Just as the conductor keeps the musicians in sync and identifies which instruments are playing at which times, FFT helps regulate how data frequencies interact and ensuring they operate without interference.
Advantages of FFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β’ Speed: Extremely fast compared to direct DFT computation.
β’ Accuracy: Enables precise frequency resolution.
β’ Versatility: Useful in both hardware and software implementations.
β’ Real-time Processing: Supports live systems like audio/video streaming and SDR (Software Defined Radio).
Detailed Explanation
FFT comes with numerous advantages compared to traditional DFT calculations. Its speed is a significant benefit, allowing for rapid computations needed in real-time applications. Accuracy is another crucial aspect, as FFT provides detailed frequency resolution that is essential for effective analysis. The versatility of FFT means it can be implemented in various environments, from dedicated hardware to software applications, making it widely applicable across different fields. This versatility also extends to real-time processing capabilities, permitting its use in streaming media applications and Software Defined Radio (SDR) setups.
Examples & Analogies
Consider FFT like a high-tech calculator compared to a traditional abacus. The calculator can perform complex equations extremely quickly and allows for precise answers, while the abacus, although still useful, is much slower and less accurate for complex calculations. In the same way, FFT provides a faster and more accurate method for analyzing signals.
Limitations and Considerations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β’ Signal length should be a power of 2 for optimal performance.
β’ Spectral leakage can occur due to discontinuities in non-periodic signals β mitigated by windowing (e.g., Hamming, Hanning windows).
β’ Limited by sampling rate: Nyquist theorem must be respected.
Detailed Explanation
While FFT presents powerful advantages, it is important to understand its limitations. One key consideration is that the length of the signal (the number of samples) should ideally be a power of 2 to achieve optimal performance. Additionally, spectral leakage can occur when the signal is not periodic within the observation window, leading to inaccuracies. This can often be mitigated by applying window functions like Hamming or Hanning, which smooth out discontinuities. Finally, the sampling rate must adhere to the Nyquist theorem, which states that to accurately capture a signal, the sampling rate must be at least twice the highest frequency present in the signal.
Examples & Analogies
Think about baking a perfect cake, where the ingredients need to be precisely measured and mixed. Using a container that is too small (not a power of 2) can lead to overflow and mess, while not stirring ingredients properly can cause the batter (signal) to be inconsistent in mixing. Similarly, the Nyquist theorem ensures you capture the full flavor of each ingredient (frequency) without missing any important parts.
Summary
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The FFT is a highly efficient algorithm for computing the frequency content of a signal.
It enables spectral analysis in real-time by transforming signals from the time domain to the frequency domain.
Widely used in communication systems for modulation analysis, channel estimation, and interference detection.
Understanding the FFT is key to implementing digital communication and DSP-based systems.
Detailed Explanation
In summary, the Fast Fourier Transform (FFT) is recognized for its efficiency in computing the frequency components of signals. It facilitates real-time spectral analysis by converting signals between time and frequency domains, making it indispensable in various communication applications, including modulation analysis, channel assessment, and interference detection. A solid comprehension of FFT principles is essential for anyone looking to implement digital communication or digital signal processing (DSP) systems effectively.
Examples & Analogies
Picture FFT as a modern GPS system for navigating signals in the complex landscape of data transmission. Just like a GPS helps you find your best route efficiently, the FFT guides engineers to analyze and enhance signals, ensuring that information reaches its destination accurately and quickly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Spectral Analysis: The decomposition of signals into frequency components.
-
Fourier Transform: A mathematical tool that converts time-domain signals to frequency-domain.
-
Discrete Fourier Transform: The digital form of the Fourier Transform for finite signals.
-
Fast Fourier Transform: An efficient calculation method for DFT, allowing real-time analysis.
-
Applications in Communication Systems: FFT's role in modulation, channel analysis, and noise detection.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using FFT for audio signal processing to identify sound frequencies.
-
Applying FFT in a radar system for analyzing reflection signals.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
FFT and DFT, quick and easy to see, turn time signals into frequencies happily!
π Fascinating Stories
-
Imagine a DJ mixing tracks; they listen to sounds (time domain) and need to see the beat drops (frequency domain) to play the right music at the right time. FFT helps DJs keep the party alive!
π§ Other Memory Gems
-
Remember FFC for 'Fast Fourier Computation' β makes signal processing quick and neat.
π― Super Acronyms
Use **SPEED** to remember FFT benefits
- Speed
- Precision
- Efficiency
- Easy setup
- Direct applications.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Spectral Analysis
Definition:
The process of decomposing a signal into its frequency components.
-
Term: Time Domain
Definition:
A representation of a signal as it varies over time.
-
Term: Frequency Domain
Definition:
A representation of a signal in terms of its sinusoidal components.
-
Term: Fourier Transform (FT)
Definition:
A mathematical transform that converts a time-domain signal into its frequency-domain representation.
-
Term: Discrete Fourier Transform (DFT)
Definition:
The sampled version of the Fourier Transform, applied to discrete signals.
-
Term: Fast Fourier Transform (FFT)
Definition:
An efficient algorithm to compute the DFT, significantly reducing computational complexity.
-
Term: Nyquist Theorem
Definition:
A principle stating that to accurately sample a signal, it must be sampled at more than twice its highest frequency.