Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore the Fast Fourier Transform, commonly known as FFT. Can anyone tell me what the main purpose of the FFT is?
Isn't it used to analyze signals in the frequency domain?
Exactly! The FFT allows us to convert time-domain signals into frequency-domain representations efficiently. This is crucial for identifying the frequency components of a signal quickly.
What makes FFT different from the standard Fourier Transform?
Good question! While Fourier Transform is a general method, FFT is an optimized algorithm that significantly reduces computational complexity from O(NΒ²) to O(N log N).
Does this mean we can analyze larger signals in real time?
Yes! This efficiency enables us to perform real-time analysis, especially in applications like audio processing and communications.
Popular FFT Algorithms
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's dive into some of the popular algorithms used in the FFT. Can anyone name one?
Is Cooley-Tukey the most common one?
Yes, exactly! The Cooley-Tukey algorithm is widely used for its recursive approach. Can anyone explain what a radix-2 FFT is?
Itβs when the number of samples is a power of two, right?
Correct! The Radix-2 is efficient under this circumstance. What about Radix-4?
I think it can handle lengths that are also powers of four.
Right again! Different algorithms can optimize performance based on the signal length.
Input Requirements and Recursive Functionality
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's discuss the input requirements for FFT. Who can tell me what these requirements are?
The number of samples should be a power of two.
Exactly! This is crucial for optimal performance, particularly with the Radix-2 FFT. Can anyone describe how the FFT operates on the data?
It breaks the signal into smaller parts recursively?
Correct! FFT leverages the periodic properties of complex exponentials to combine results efficiently, which is a key aspect of its performance. How does this relate to our earlier discussions on computational complexity?
It reduces processing time significantly!
Exactly! Itβs all about making complex calculations manageable.
Applications of FFT
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's explore some applications of the FFT. Where do you think we could apply this technology?
In audio processing like MP3 encoding?
Exactly! It's pivotal in audio compression techniques. Any other thoughts?
How about in communication systems for analyzing signals?
Correct! FFT is also used for modulation and demodulation, channel response analysis, and even in radar systems.
Can we use it to detect noise?
Yes, it helps spot unwanted frequencies in a spectrum, which is a significant advantage.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The FFT allows for real-time spectral analysis of large signals by efficiently calculating the frequency components of a signal. It reduces the computational complexity from O(N^2) to O(N log N), facilitating widespread applications in various fields such as communications, audio processing, and biomedical engineering.
Detailed
Fast Fourier Transform (FFT)
The Fast Fourier Transform (FFT) is a powerful algorithm that efficiently computes the Discrete Fourier Transform (DFT) of a signal. By reducing computational complexity from O(NΒ²) to O(N log N), the FFT enables real-time analysis of large datasets, making it indispensable in various applications, including communications, audio processing, and biomedical signal analysis.
Popular FFT Algorithms
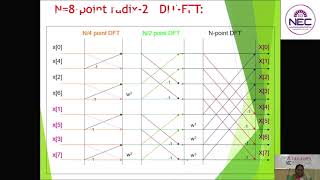
- Cooley-Tukey FFT: The most commonly used algorithm for FFT, which divides the computation recursively into smaller parts.
- Radix-2 and Radix-4 FFT: Algorithms optimized based on the power of 2 or 4 in the signal length.
Key Characteristics
- Recursive Approach: The FFT breaks down a signal into smaller parts, utilizing the symmetry properties of complex exponential functions to efficiently combine results.
- Input Requirements: For optimal performance with the Radix-2 FFT, the number of samples (N) must be a power of 2.
Overall, the FFT is essential for efficient spectral analysis, enhancing the understanding of signal behavior in both time and frequency domains.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to FFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β FFT is an efficient algorithm to compute the DFT.
Detailed Explanation
The Fast Fourier Transform (FFT) is a computational technique used to calculate the Discrete Fourier Transform (DFT) more efficiently. The DFT is vital for analyzing signals in the frequency domain, but it can be computationally expensive. The FFT reduces the time complexity significantly, making it practical for real-time applications.
Examples & Analogies
Consider how you can quickly find a name in a phone book by flipping through the pages instead of writing down every name in sequence. The FFT does a similar thing: it quickly finds frequency components in a signal without having to calculate each one from scratch.
Complexity Reduction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Reduces complexity from O(N^2) to O(N log N)
Detailed Explanation
In computational terms, complexity refers to the amount of resources (like time or memory) needed to perform a task as the size of the input increases. The DFT has a complexity of O(N^2), meaning the time it takes grows quadratically with the number of samples. The FFT reduces this to O(N log N), which is a significant improvement. This means that as the number of samples increases, the computation remains manageable and quicker.
Examples & Analogies
Imagine sorting a large box of mixed-up socks. If you went through one by one to find a pair, it would take time that gets longer with each added sock (O(N^2)). But if you used an efficient method, like using color and type to group them, you could do it much faster despite having the same number of socks (O(N log N)).
Real-Time Spectral Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Enables real-time spectral analysis of large signals.
Detailed Explanation
One of the standout features of the FFT is its ability to analyze large signals in real-time. This means that as a signal is being received, the FFT can process it quickly enough to provide immediate feedback on its frequency content. This capability is critical in applications such as audio processing and telecommunications where timely information can influence system performance.
Examples & Analogies
Think of a real-time traffic update system that uses cameras and sensors to analyze traffic flow instantly. Just as the system updates its data in real-time to manage traffic better, the FFT also processes signal information on-the-fly, allowing for immediate analysis.
Popular FFT Algorithms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β Popular FFT Algorithms:
β Cooley-Tukey FFT (most common)
β Radix-2, Radix-4 algorithms (based on signal length)
Detailed Explanation
Several algorithms have been developed to implement FFT efficiently. The most widely used is the Cooley-Tukey algorithm, which works best with signals whose length is a power of 2. Other variations include Radix-2 and Radix-4 FFTs, which optimize the computation further based on the length of the input signal. Understanding these algorithms allows for selecting the appropriate method based on the specific application needs.
Examples & Analogies
Imagine you're baking and you have a recipe that can be adjusted for different batch sizes. Just like choosing the right batch size affects how you mix and bake, choosing the right FFT algorithm based on the size of the signal can optimize performance and reduce processing time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
FFT: An efficient algorithm for computing the Discrete Fourier Transform.
-
Computational Complexity: Reduction from O(NΒ²) to O(N log N).
-
Real-Time Analysis: Enables efficient analysis of large signals.
-
Popular Algorithms: Cooley-Tukey, Radix-2, Radix-4.
-
Input Requirements: N must be a power of two for optimal performance.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using FFT in audio processing to determine the frequency spectrum of a musical piece.
-
Applying FFT in telecommunications to analyze signals for modulation and demodulation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
FFT makes calculations light, analyzing signals fast and bright.
π― Super Acronyms
F.A.S.T. - Fast Algorithm for Signal Transformations.
π Fascinating Stories
-
Imagine a wizard who can quickly analyze the magic (frequency) within musical notes, using his special spell of the FFT to conjure up insights at lightning speed.
π§ Other Memory Gems
-
Remember the steps of FFT: 1) Split, 2) Transform, 3) Combine, and 4) Analyze.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fast Fourier Transform (FFT)
Definition:
An efficient algorithm to compute the Discrete Fourier Transform (DFT), reducing the computational complexity.
-
Term: Discrete Fourier Transform (DFT)
Definition:
A mathematical transform that converts a sequence of values into components of different frequencies.
-
Term: CooleyTukey Algorithm
Definition:
The most widely used algorithm for computing the FFT through recursive decomposition.
-
Term: Radix2 FFT
Definition:
An FFT algorithm efficient when the number of samples is a power of two.
-
Term: Radix4 FFT
Definition:
An FFT algorithm that is optimized for input lengths that are powers of four.