3.2 - Graphical Method of Solution of a Pair of Linear Equations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Linear Equations and Solutions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re going to discuss how to graphically solve pairs of linear equations. Can anyone tell me what a linear equation in two variables looks like?

Is it like 'y = mx + b'? The equation of a line?

Exactly! In such equations, 'm' represents the slope and 'b' represents the y-intercept. Now, how can we visualize these equations?

By plotting them on a graph!

Correct! And when we plot two linear equations, we can find their intersection point, right? This point indicates the solution to the equations.

So, if the lines intersect, there's one unique solution!

That's right! If they are parallel, would there be a solution?

No, because they never meet!

Great! Remember, we will call lines that don't intersect 'inconsistent' equations. Summarizing, if lines meet, we have a unique solution, if they are parallel, it's inconsistent.
Analyzing Coefficients
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's now compare coefficients! Can anyone explain what it means when we say equations are equivalent?

I think it means they represent the same line, so they have infinitely many solutions!

Exactly! For a pair of linear equations represented in standard form, how would we recognize if they're equivalent?

If the ratios of their coefficients are equal!

Right! So if we have two equations with coefficients in the form of `a₁x + b₁y + c₁ = 0` and `a₂x + b₂y + c₂ = 0`, what must hold true for them to be dependent?

If a₁/a₂ = b₁/b₂ = c₁/c₂!

Excellent! This analysis helps us understand not only the geometric behavior of lines, but also their algebraic interdependencies.
Practical Examples and Graphs
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

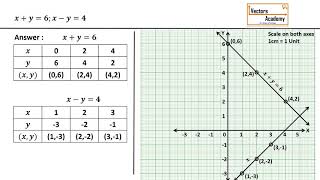
Let’s put our knowledge to practice! Who can graph the equations `x - 2y = 0` and `3x + 4y = 20` for me?

I can! I’ll rewrite them in slope-intercept form and plot the lines.

Can I help? We can find their intersection point together!

Great teamwork! After plotting, what do we expect if they intersect?

There will be a unique point, the solution!

Good job! How would we determine if they are consistent or inconsistent?

By checking if one is parallel or if they overlap completely!

Perfect! Understanding practical application helps solidify these concepts.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The graphical method provides a visual approach to solving pairs of linear equations, characterized by three primary scenarios: unique solutions, no solutions, and infinitely many solutions. The section further explains the relationships between the graphical representation of equations and their solutions.
Detailed
Graphical Method of Solution of a Pair of Linear Equations
In this section, we explore the graphical method for solving linear equations in two variables. Specifically, a pair of linear equations can result in three different scenarios:
- Unique Solution: The lines intersect at a single point, indicating a consistent pair of equations.
- No Solution: The lines are parallel, suggesting the equations are inconsistent.
- Infinitely Many Solutions: The lines coincide, which means the equations are dependent and consistent.
To illustrate these concepts, we analyze pairs of equations through examples, comparing coefficients to determine the relationships between the equations. Our discussion includes graphical representations of the equations, using coordinate planes to plot solutions visually and confirm whether the equations are consistent or inconsistent based on their alignment.
Example pairs of linear equations are provided to demonstrate conditions under which solutions exist or do not. By understanding these relationships through graphical representation, students can gain insights into the behavior of linear equations and refine their skills in graphical analysis.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Types of Linear Equations
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A pair of linear equations which has no solution, is called an inconsistent pair of linear equations. A pair of linear equations in two variables, which has a solution, is called a consistent pair of linear equations. A pair of linear equations which are equivalent has infinitely many distinct common solutions. Such a pair is called a dependent pair of linear equations in two variables. Note that a dependent pair of linear equations is always consistent.
Detailed Explanation
In linear equations, we can categorize our equations into three types based on their solutions. An inconsistent pair indicates no solution exists, meaning the lines representing the equations do not intersect at any point. A consistent pair means there is at least one solution, typically being two lines that intersect at a single point. Lastly, dependent pairs imply that the two lines overlap entirely, giving us many solutions as every point along the line is valid.
Examples & Analogies
Imagine a scenario where two people are looking for common ground to meet. If one person states they can only be at location A, and the other states they will only be at location B (which is far away), it’s like our inconsistent pairs, where meeting is impossible. However, if both can meet at one park (the solution), that’s akin to a consistent pair. Finally, if both agree to meet anywhere along the same path (dependent pair), that means we have countless meeting points.
Graphical Representation of Linear Equations
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We can now summarise the behaviour of lines representing a pair of linear equations in two variables and the existence of solutions as follows:
(i) the lines may intersect in a single point. In this case, the pair of equations has a unique solution (consistent pair of equations).
(ii) the lines may be parallel. In this case, the equations have no solution (inconsistent pair of equations).
(iii) the lines may be coincident. In this case, the equations have infinitely many solutions [dependent (consistent) pair of equations].
Detailed Explanation
When we graph linear equations, we observe how the lines behave in relation to each other. If two lines cross at a point, that point represents the unique solution to the equations. If they run parallel, they will never meet, indicating no solutions exist. In contrast, if the lines lie on top of each other, they are equivalent, and any point on the line is a solution.
Examples & Analogies
Think of a busy intersection: the crossing of the roads represents the unique solution as cars can only meet at that point. Parallel roads are like two friends who live on the same street but never cross paths, while shared lanes or paths indicate they can go anywhere together—every point along the way is an option.
Examining Example Pairs of Equations
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider the following three pairs of equations:
(i) x – 2y = 0 and 3x + 4y – 20 = 0 (The lines intersect)
(ii) 2x + 3y – 9 = 0 and 4x + 6y – 18 = 0 (The lines coincide)
(iii) x + 2y – 4 = 0 and 2x + 4y – 12 = 0 (The lines are parallel)
Detailed Explanation
In these examples, we are looking at specific pairs of equations. The first pair of equations intersect, indicating a unique solution exists. The second pair represents coincident lines, meaning there are infinitely many solutions since every point on the line is a solution to both equations. Finally, the third pair is parallel and signifies that no solutions can be found as they will never meet.
Examples & Analogies
Imagine three scenarios: in the first, two friends meet at a coffee shop (the intersecting lines). In the second scenario, twins are always together (coincident means every moment together can be shared). In the third, two friends on different subway lines—regardless of how often they travel, they will never meet (parallel lines)!
Understanding the Ratios of Coefficients
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
From the table above, you can observe that if the lines represented by the equation ax + by + c = 0 and ax + by + c = 0 are (i) intersecting, then a1 ≠ a2. (ii) coincident, then a1 = a2 = c1. (iii) parallel, then a1 = a2 ≠ c1.
Detailed Explanation
The properties of the coefficients (a1, b1, c1) give insight into the relationships between the two lines. If the ratios are different for 'a', the lines intersect. If they are equal for 'a' and 'b' but have different 'c' values, the lines are parallel. Lastly, if all three ratios are equal, it indicates the lines are coincident.
Examples & Analogies
Think of these coefficients as ingredients in a recipe. If you have the same ingredients in the same amount (coincident), you get the same dish (infinite solutions). If the amounts are different but the ingredients are the same (intersecting), you will create different dishes but share some parts. Lastly, if you use completely different ingredients (parallel), you won’t be able to make something similar at all.
Graphical Verification of Equations
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us now consider some more examples to illustrate it.
Detailed Explanation
We can use equations to demonstrate how to find solutions graphically. By plotting the equations on a coordinate plane, we can visually see where they intersect, indicating the solution to the pair of equations. If they don’t intersect, we can conclude there are no solutions, and if they coincide, we can state there are infinitely many solutions.
Examples & Analogies
Imagine a treasure map with two different trails marked by two friends looking for treasure. If their paths cross at a single point, they found the treasure! If one friend’s trail overlaps with the other, then they will find treasure everywhere along that path. But if they are walking on two completely different paths with no intersection, they will never uncover the treasure together.
Key Concepts
-
Graphical Representation: Visualizing linear equations on a coordinate plane.
-
Intersection Points: Determining solutions through points where lines cross.
-
Types of Solutions: Distinguishing between unique solutions, no solutions, and infinitely many solutions based on graph characteristics.
Examples & Applications
The equations y = x and y = 2x intersect at the point (0,0), which is the unique solution.
The equations y = x and y = x + 1 are parallel and have no solutions.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When lines do meet at just one point, the solution is set, that’s their joint.
Stories
Imagine two friends, Alice and Bob, walking along parallel paths. They chat but never meet. They're like equations that never intersect!
Memory Tools
C.I.N. for solutions: C for Consistent (unique), I for Inconsistent (none), N for Notably dependent (infinitely many).
Acronyms
P.U.C. for line relationships
for Parallel lines
for Unique intersection
for Coincident lines.
Flash Cards
Glossary
- Linear Equation
An equation that represents a straight line when plotted on a graph.
- Unique Solution
A condition where two lines intersect at exactly one point.
- Inconsistent Equations
Two linear equations that have no solutions, typically represented by parallel lines.
- Dependent Equations
A pair of linear equations that have infinitely many solutions, where one equation is a multiple of the other.
- Coefficients
Numbers that multiply the variables in an equation, indicating the relationship between variables.
Reference links
Supplementary resources to enhance your learning experience.
