Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Substitution Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to learn about the Substitution Method, an essential technique for solving pairs of linear equations. Can anyone tell me what you understand by linear equations?
Linear equations are equations of the first degree, meaning they only have variables raised to the first power.
Exactly! And with linear equations, we often deal with two variables, like x and y. The Substitution Method allows us to solve these equations efficiently. Does anyone know how we start?
We need to isolate one variable first, right?
Correct! Let's say we have the equations 7x - 15y = 2 and x + 2y = 3. If we isolate x from the second equation, we get x = 3 - 2y. This will be our first step.
Using the Substitution Method: Solving an Example
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, using the expression x = 3 - 2y, we can substitute this value into the first equation. This gives us 7(3 - 2y) - 15y = 2. Can someone help me solve this?
Yes! Distributing 7 gives us 21 - 14y - 15y = 2, which simplifies to 21 - 29y = 2.
Great! Now, let's isolate y. What do we get?
Subtract 21 from both sides: -29y = 2 - 21, so -29y = -19!
Exactly, and that leads us to y = 19/29. Now, how can we find x?
We substitute y back into x = 3 - 2y.
Verification of Solutions
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we have both values, x = 49/29 and y = 19/29, why is it important to verify our solutions?
To make sure that our solutions actually satisfy both original equations.
Correct! We can substitute both x and y into the first equation to see if it holds true. Let's check this. Who can help with that?
Substituting gives us 7(49/29) - 15(19/29), and if it simplifies to 2, then our answer is correct.
Wonderful! Verification confirms that our method is indeed reliable. Always remember to check your work!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the Substitution Method, a systematic approach to solving pairs of linear equations. By rearranging one equation to isolate a variable and substituting that expression into the other equation, we can find the values of both variables. The section includes several examples and emphasizes the importance of verification after obtaining the solution.
Detailed
Substitution Method in Linear Equations
The Substitution Method is a powerful algebraic technique for solving a pair of linear equations. It allows one to find the values of variables by expressing one variable in terms of the other and then substituting that expression into the second equation. Here are the primary steps and components involved in this method:
Key Steps:
- Isolate a variable: Choose one of the two equations and solve for one variable in terms of the other. This is often easier if the equation is already in a form that allows easy isolation.
- Substitution: Substitute the expression obtained for one variable into the other equation. This will yield an equation with only one variable which can be solved easily.
- Finding both variables: Once one variable is solved, substitute this value back into one of the original equations to find the second variable.
- Verification: It is crucial to substitute both values back into the original equations to ensure they satisfy both equations.
Importance:
The Substitution Method not only provides a systematic way to solve linear equations but also enhances understanding of relationships between variables. By utilizing this method, learners gain familiarity in manipulating algebraic expressions and equations, setting a foundation for more complex algebraic concepts.
Youtube Videos
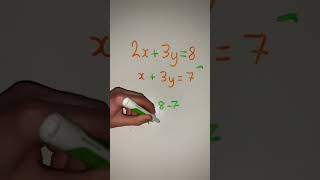
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Example 4: Solving Equations by Substitution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 4 : Solve the following pair of equations by substitution method:
7x β 15y = 2 (1)
x + 2y = 3 (2)
Solution :
Step 1 : We pick either of the equations and write one variable in terms of the other. Let us consider the Equation (2) :
x + 2y = 3
and write it as x = 3 β 2y (3)
Step 2 : Substitute the value of x in Equation (1). We get
7(3 β 2y) β 15y = 2
i.e., 21 β 14y β 15y = 2
i.e., β29y = β19
Therefore, y = 19/29
Step 3 : Substituting this value of y in Equation (3), we get
x = 3 β 2(19/29)
i.e., x = (49/29)
Therefore, the solution is x = 49/29, y = 19/29.
Verification : Substituting x = 49/29 and y = 19/29, you can verify that both the Equations (1) and (2) are satisfied.
Detailed Explanation
In this example, we solved a pair of equations using the substitution method. We took the second equation, expressed x in terms of y, and substituted that expression into the first equation. This way, we reduced the problem to finding just one variable (y) and then used that value to find the other variable (x). This approach is very systematic and helps to avoid confusion when solving equations.
Examples & Analogies
Imagine you want to make a recipe for a cake, but the recipe mentions an ingredient that you can buy in different quantities. You decide how much of that ingredient you want to buy first (this is like rewriting one variable), and then you calculate how much of the other ingredients you'll need based on that choice (this is like substituting into the other equation).
Understanding the Substitution Method Steps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Step 1 : Find the value of one variable, say y in terms of the other variable, i.e., x from either equation, whichever is convenient.
Step 2 : Substitute this value of y in the other equation, and reduce it to an equation in one variable, i.e., in terms of x, which can be solved. Sometimes, as in Examples 9 and 10 below, you can get statements with no variable. If this statement is true, you can conclude that the pair of linear equations has infinitely many solutions. If the statement is false, then the pair of linear equations is inconsistent.
Step 3 : Substitute the value of x (or y) obtained in Step 2 in the equation used in Step 1 to obtain the value of the other variable.
Remark : We have substituted the value of one variable by expressing it in terms of the other variable to solve the pair of linear equations. That is why the method is known as the substitution method.
Detailed Explanation
This chunk outlines the general steps of the substitution method clearly. The first step involves solving one equation for one variable. The second step is to insert this expression into the other equation, which will give you a single-variable equation that can be solved easily. Finally, you substitute back the value obtained to find the other variable. Recognizing these steps can make the substitution method very systematic and easy to implement.
Examples & Analogies
Think of a puzzle where you are trying to find the location of two hidden keys in a room based on the clues. First, you use one clue to find out what one key's location might be in terms of the other key's location. Then, you substitute that guess into the other clue to narrow it down until you have exact locations for both keys.
Example 5: Aftab's Age Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 5 : Solve the following questionβAftab tells his daughter, βSeven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.β
Solution : Let s and t be the ages (in years) of Aftab and his daughter, respectively. Then, the pair of linear equations that represent the situation is
s β 7 = 7(t β 7), i.e., s β 7t + 42 = 0 (1)
and s + 3 = 3(t + 3), i.e., s β 3t = 6 (2)
Using Equation (2), we get s = 3t + 6. Putting this value of s in Equation (1), we get
(3t + 6) β 7t + 42 = 0,
i.e., 4t = 48, which gives t = 12.
Putting this value of t in Equation (2), we get s = 3(12) + 6 = 42. So, Aftab and his daughter are 42 and 12 years old, respectively.
Detailed Explanation
In this example, we started by creating equations based on the information given about the ages of Aftab and his daughter. By defining their ages in terms of variables, we could set up relationships based on the statements provided. We rearranged one equation to express one variable in terms of another, made substitutive calculations to isolate the variables, and thus determined their ages step-by-step. This practical application illustrates the substitution method's effectiveness in solving real-life problems.
Examples & Analogies
Imagine youβre trying to figure out how old you and your friend were at different points in time based on the conversations you have. Just like Aftab describes relationships between his age and his daughterβs age over time, you might calculate the ages using their talks, gradually working backwards through the clues until you have the answer.
Example 6: Cost of Pencils and Erasers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 6 : In a shop the cost of 2 pencils and 3 erasers is 9 and the cost of 4 pencils and 6 erasers is18. Find the cost of each pencil and each eraser.
Solution : The pair of linear equations formed were:
2x + 3y = 9 (1)
4x + 6y = 18 (2)
We first express the value of x in terms of y from the equation 2x + 3y = 9, to get x = (9β3y)/2 (3)
Now we substitute this value of x in Equation (2), to get
4((9β3y)/2) + 6y = 18
i.e., 18 β 6y + 6y = 18
i.e., 18 = 18.
This statement is true for all values of y. However, we do not get a specific value of y as a solution. Therefore, we cannot obtain a specific value of x. This situation has arisen because both the given equations are the same. Therefore, Equations (1) and (2) have infinitely many solutions.
Detailed Explanation
In this example, after forming the equations based on the cost of pencils and erasers, we found that both equations were equivalent, meaning they represented the same line on a graph. This leads to infinitely many solutions, suggesting there are many combinations of costs for pencils and erasers that satisfy the equations. Understanding when equations yield infinite solutions is critical to using the substitution method effectively, as it shows that certain problem setups may not yield unique answers.
Examples & Analogies
Imagine you are at a market and notice that various combinations of items (like fruits) can all add up to the same cost. If two stores sell the same items but at different prices, you might find countless ways to buy those items together for that total cost. This scenario mirrors the infinitely many solutions observed through the equations in the pencil and eraser problem.
Example 7: Crossing Rails Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 7 : Two rails are represented by the equations
x + 2y β 4 = 0 and 2x + 4y β 12 = 0. Will the rails cross each other?
Solution : The pair of linear equations formed were:
x + 2y β 4 = 0 (1)
2x + 4y β 12 = 0 (2)
We express x in terms of y from Equation (1) to get x = 4 β 2y.
Now, we substitute this value of x in Equation (2) to get
2(4 β 2y) + 4y β 12 = 0
i.e., 8 β 12 = 0
i.e., β 4 = 0
which is a false statement.
Therefore, the equations do not have a common solution. So, the two rails will not cross each other.
Detailed Explanation
In this example, we set out to determine whether two lines represented by equations would intersect. Upon substitution into our equations, we arrived at a false statement, indicating inconsistency between the statements provided in the equations. This demonstrates a situation where graphical interpretation may lead to clear conclusions about the relationships between variables β in this case, that the lines do not cross.
Examples & Analogies
Think of two trains on parallel tracks. You know the paths will never meet up based on their routes and times, just like these equations indicated they wouldnβt intersect. Realizing that some routes simply wonβt cross helps clarify the understanding of relationships in linear equations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Isolating a variable: A crucial step in the substitution method where one variable is expressed in terms of another.
-
Substituting values: Inserting the expression of the isolated variable into the other equation to solve for the remaining variable.
-
Verification: The process of checking if the obtained solutions satisfy the original equations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Solve 7x - 15y = 2 and x + 2y = 3 using substitution.
-
Example 2: Aftab and his daughter's age problem utilizing substitution method to establish linear equations for their ages.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Substitution, it's no illusion, solve equations in a truer fashion.
π Fascinating Stories
-
Once there was a wise old owl who taught students to express their thoughts clearly. She always started with isolating a variable, then asked them to substitute their ideas into the world of equations.
π§ Other Memory Gems
-
I.S.S.V. - Isolate, Substitute, Solve, Verify.
π― Super Acronyms
S.O.S. - Substitute, Obtain, Solve.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Substitution Method
Definition:
An algebraic method of solving linear equations by substituting a variable's value from one equation into the other.
-
Term: Linear Equation
Definition:
An equation that graphs as a straight line and can be expressed in the form ax + by = c.
-
Term: Isolate
Definition:
To express one variable in terms of others, typically to prepare for substitution.