Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Discriminants
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we're going to discuss the nature of roots in quadratic equations. Who can remind us of the general form of a quadratic equation?

Isn't it ax² + bx + c = 0?

Exactly! Now, the discriminant, D, is crucial here, calculated as D = b² - 4ac. Can someone tell me why D is important?

It tells us about the nature of the roots!

Right! If D > 0, we have two distinct real roots. Can anyone suggest how we calculate those roots?

We use the quadratic formula!

Correct! We can find the two roots using x = (-b ± √D) / 2a. Can someone repeat what happens if D = 0?

Then we have two equal real roots!

Exactly! And when D is less than zero, what does that mean?

There are no real roots!

Very well! So reviewing the discriminant helps us predict and visualize real-life scenarios.
Example Analysis
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Okay, let’s work through an example: Find the discriminant of 2x² - 4x + 3. Can someone identify a, b, and c?

Here, a = 2, b = -4, and c = 3.

Correct! Now, what is D?

D = (-4)² - 4(2)(3) = 16 - 24 which equals -8.

Excellent! Since D < 0, what can we conclude about the roots?

There are no real roots!

Fantastic! Let’s move on to another example. How about we check for the equation 3x² - 2x + 1/3?

Let’s find a, b, and c!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the conditions under which quadratic equations have distinct real roots, equal real roots, or no real roots, emphasizing the role of the discriminant. It also includes examples and applications related to these concepts.
Detailed
Nature of Roots in Quadratic Equations
The nature of the roots of a quadratic equation of the form ax² + bx + c = 0 can be determined using the discriminant, denoted as D = b² - 4ac. The value of the discriminant reveals significant information about the roots:
- Two Distinct Real Roots: If D > 0, the quadratic equation has two distinct real roots. The roots can be calculated using the formulas:
- Two Equal Real Roots: If D = 0, the quadratic equation has exactly two equal real roots given by:
- No Real Roots: If D < 0, there are no real roots for the quadratic, reflecting that the associated values do not intersect with the x-axis; thus no real solution exists.
Key Takeaway: Understanding the discriminant not only allows us to solve quadratic equations but also equips us to interpret various real-life contexts, such as physics and finance, where solutions are necessary for decision-making.
Youtube Videos



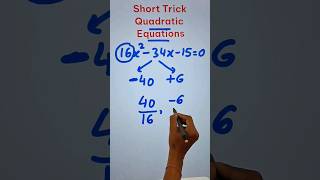






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Quadratic Formula Basics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The equation ax² + bx + c = 0 are given by
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
Detailed Explanation
This chunk introduces the quadratic formula that is used to find the roots of a quadratic equation of the form ax² + bx + c = 0. The formula shows how to calculate the roots (
'values' of x) based on the coefficients a, b, and c from the quadratic equation. The '±' symbol indicates that there can be two possible results for x, which correspond to the two potential solutions (roots) of the equation.
Examples & Analogies
Think of the quadratic equation like a path that branches off into two different routes. The quadratic formula tells you how to find the point at which you can make a choice between these two paths, represented by the two solutions for x, which can lead to different outcomes.
Discriminant and Root Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If b² - 4ac > 0, we get two distinct real roots.
If b² - 4ac = 0, then the roots are equal (two equal real roots).
If b² - 4ac < 0, then there are no real roots.
Detailed Explanation
In this chunk, we discuss the discriminant (b² - 4ac), which is a key value that indicates the nature of the roots of the quadratic equation. Specifically: 1. If the discriminant is greater than 0, this means the quadratic has two different real roots. 2. If the discriminant is exactly 0, the quadratic has one real root that is counted twice (commonly called repeated roots). 3. If the discriminant is less than 0, there are no real roots—this means that the solutions involve complex numbers.
Examples & Analogies
Imagine you're throwing a ball in the air. The different outcomes of where the ball will land (i.e., will it bounce twice? will it land in the ground without bouncing? or will it lift off into a different dimension?) can be compared to the types of roots depending on the discriminant's value.
Example of Discriminant Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 7: Find the discriminant of the quadratic equation 2x² - 4x + 3 = 0, and hence find the nature of its roots.
Solution: The given equation is of the form ax² + bx + c, where a = 2, b = -4, c = 3. Therefore, the discriminant
b² - 4ac = (-4)² - (4 × 2 × 3) = 16 - 24 = -8 < 0.
So, the given equation has no real roots.
Detailed Explanation
This example illustrates how to compute the discriminant for a specific quadratic equation to determine its nature. By substituting the coefficients from the quadratic equation into the discriminant formula, we can find that the result is -8, which implies that the quadratic equation has no real roots. This step is fundamental in understanding how to analyze the nature of different quadratic equations.
Examples & Analogies
Think of trying to find a treasure map. If you find the map leads to a spot underwater (like having no real roots), it wouldn't be possible to reach the treasure (real solutions) with normal means—indicating the treasure isn’t there in the real world.
Practical Application of Roots in Geometry
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 8: A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres.
... So, the distance ‘x’ of the pole from gate B satisfies the equation x² + 7x - 60 = 0...
Detailed Explanation
In this example, we analyze a practical situation involving placements in geometry, using the quadratic equation derived from the conditions given (distances to gates). After setting up the equation based on the scenario, we find the discriminant to determine the feasibility of placing the pole according to the conditions. It concludes whether the arrangement at that specific point is viable based on the quadratic roots.
Examples & Analogies
Imagine you are setting up tents along a line (the boundary of the park) between two markers (the gates). Depending on how far apart the markers are and the rules you've set (like the 7-meter distance), you need to calculate the exact spots to set up your tents to ensure they fit without breaking the rules.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Discriminant: A value that determines the nature of roots of quadratic equations.
-
Distinct Real Roots: Occur when the discriminant is positive.
-
Equal Real Roots: Occur when the discriminant is zero.
-
Complex Roots: Indicate a situation where there are no real roots, denoted by a negative discriminant.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example calculating D for the equation 2x² - 4x + 3 and interpreting D < 0 means no roots.
-
Example finding real roots for the equation 3x² - 2x + 1/3 and interpreting D > 0 means two distinct roots.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
D for discriminant, roots so bright, distinguish them easy, day or night.
📖 Fascinating Stories
-
In a land where mathematicians lived happily, one day they found a magical word: 'discriminant.' It helped them determine the fate of their equations—whether they’d yield treasures (roots) or leave them empty-handed (no roots).
🧠 Other Memory Gems
-
Remember D for discriminant: D > 0 means two roots, D = 0 means one root, D < 0 means no roots. Think of a tree—roots, for life!
🎯 Super Acronyms
D = Distinct, Equal, Not. Remember the roots I sought!
Flash Cards
Review key concepts with flashcards.
