Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Quadratic Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we will explore quadratic equations. A quadratic equation is typically in the form ax² + bx + c = 0. Can anyone tell me what qualifies a polynomial to be quadratic?

Is it because the highest power of x is 2?

Exactly! The highest degree must be 2. Now, why can't a in this equation be zero?

Because if a is 0, then it would not be a quadratic equation anymore?

Correct! Well done. Now let’s move on to the roots of a quadratic equation. What is meant by the roots?

The values of x that make the equation equal to zero?

Right! Roots are solutions of the equation ax² + bx + c = 0.

Can we find the roots using the quadratic formula?

Yes! The quadratic formula is x = rac{-b m + ext{√} { ext{b² - 4ac}}}{2a}. Remember it as a key method in solving quadratic equations.

To wrap up, understanding quadratic equations is crucial in mathematics, as they model various real-life situations.
Understanding Roots and Their Nature
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now, let’s delve into the nature of these roots using the discriminant. Can someone tell me what the discriminant is?

It's the value b² - 4ac from the quadratic equation, right?

Exactly! And how does the discriminant affect the number of roots?

If it's positive, there are two distinct roots?

And if it's zero, we have one repeated root!

But if the discriminant is negative, we have no real roots?

Perfectly summarized! So remember these conditions, as they are vital when working through problems involving quadratic equations.
Solving Quadratic Equations by Factorization
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Let's explore how to find the roots by factorization. Do you all remember how to split the middle term?

Yes! You find two numbers that multiply to give ac and add to give b.

Great! Let’s solve the equation 2x² - 5x + 3 = 0 together. What’s next after identifying a and b?

We need to factor it!

So we can split -5x into -2x and -3x because they multiply to 6 and add to -5.

Exactly, good job! Then we can write it as (2x - 3)(x - 1) = 0. What does that give us?

The roots are x = 1 and x = 3/2!

Fantastic! You’ve all grasped how to solve using factorization very well.
Summary and Real-Life Applications
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

As we wrap up our discussion on quadratic equations, why do you think it’s essential to study these?

Because they can describe many real-world situations like projectile motion!

And economic models, right?

Absolutely! Quadratic equations show up in areas such as physics, economics, and even engineering. How do we apply these concepts practically?

We could use them to optimize areas or find maximum revenue!

Or solve problems with specific dimensions like the prayer hall example!

Excellent! Always remember that mathematics is not just abstract; it reflects real life!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
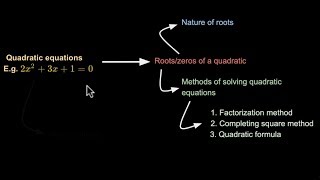
In this section, we explore the definition of quadratic equations, their roots, and methods of solving these equations, such as factorization and the quadratic formula. Additionally, we discuss how to determine the nature of the roots using the discriminant, summarizing the conditions under which quadratic equations have real roots.
Detailed
Summary of Quadratic Equations
In this chapter, we have focused on quadratic equations, which are defined as equations of the form ax² + bx + c = 0 where a, b, and c are real numbers and a ≠ 0.
- Roots Definition: A number α is termed a root of the quadratic equation if substituting it into the polynomial results in zero: aα² + bα + c = 0. The roots of the quadratic polynomial and the roots of the equation are identical.
- Methods of Solving: We can factorize quadratic equations into linear factors to find their roots and apply the quadratic formula:
- Nature of Roots: The nature of the roots of the quadratic equation can be determined using the discriminant (D = b² - 4ac). The roots can be
- Distinct real roots when D > 0
- Equal roots when D = 0
- No real roots when D < 0
This overview provides a comprehensive understanding of quadratic equations, essential for solving practical problems across various fields, highlighting their importance in both mathematics and real-world applications.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Quadratic Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A quadratic equation in the variable x is of the form ax² + bx + c = 0, where a, b, c are real numbers and a ≠ 0.
Detailed Explanation
This statement defines what a quadratic equation is. A quadratic equation must include a term with x squared (ax²), a term with x (bx), and a constant (c). The important condition is that the coefficient 'a' of the x² term cannot be zero because if it were, the equation would no longer be quadratic but linear.
Examples & Analogies
Think of a quadratic equation like a recipe that has three essential ingredients (ax², bx, and c). If one of those ingredients is missing (like 'a' being zero), then you can't make the dish (or solve the equation) as it fundamentally changes the nature of what you're making.
Roots of Quadratic Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A real number α is said to be a root of the quadratic equation ax² + bx + c = 0, if aα² + bα + c = 0. The zeroes of the quadratic polynomial ax² + bx + c and the roots of the quadratic equation ax² + bx + c = 0 are the same.
Detailed Explanation
This explains the concept of roots in relation to quadratic equations. A root is essentially a solution to the equation where substituting the value of α satisfies the equation, making it true. It’s an essential property of quadratic equations that their solutions (or roots) correspond directly with the values where their associated quadratic polynomial equals zero.
Examples & Analogies
Imagine planting trees (roots) in a garden (the equation). Each tree’s location where it can grow (the roots) corresponds to a specific spot in the garden where certain conditions (values of α) make it thrive (equate the equation to zero).
Factoring Quadratic Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If we can factorise ax² + bx + c, a ≠ 0, into a product of two linear factors, then the roots of the quadratic equation ax² + bx + c = 0 can be found by equating each factor to zero.
Detailed Explanation
This point stipulates that quadratic equations can often be simplified into two simpler equations (linear factors), like finding two numbers that when multiplied yield the original quadratic expression. By solving these simpler equations, we can find the roots of the original quadratic equation.
Examples & Analogies
Think of it like a complex puzzle that can be broken down into smaller, manageable pieces (linear factors). Once you solve each of these smaller pieces, you can reassemble the entire puzzle (solve the quadratic equation).
Quadratic Formula
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The roots of a quadratic equation ax² + bx + c = 0 are given by x = [-b ± √(b² - 4ac)] / (2a) provided b² - 4ac ≥ 0.
Detailed Explanation
This formula is a comprehensive way to find the roots of any quadratic equation, regardless of whether it can be easily factorized. It uses the coefficients of the quadratic equation to calculate the roots directly. The term b² - 4ac is known as the discriminant and determines the nature of the roots — whether they are real and distinct, real and the same, or not real at all.
Examples & Analogies
Imagine this formula as a universal tool (like a Swiss Army knife) designed to tackle various quadratics. No matter the complexity of the equation (the shape of the problem), this tool can help you find the solutions effectively.
Nature of Roots Based on Discriminant
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A quadratic equation ax² + bx + c = 0 has (i) two distinct real roots, if b² - 4ac > 0, (ii) two equal roots (coincident roots), if b² - 4ac = 0, and (iii) no real roots, if b² - 4ac < 0.
Detailed Explanation
This section explains how to determine the nature of the roots based on the discriminant (b² - 4ac). A positive discriminant indicates two different solutions (two distinct real roots), zero indicates one solution (two equal roots), and a negative discriminant indicates no real solutions (the roots are complex).
Examples & Analogies
Think of a tree. The roots either spread widely (two distinct roots), they might also merge into one solid base (equal roots), or they don’t appear in the ground at all (no real roots), indicating that the conditions weren't right for the roots to develop.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Standard Form of a Quadratic Equation: ax² + bx + c = 0, where a ≠ 0.
-
Roots: Solutions of the quadratic equation.
-
Discriminant: A formula to determine the nature of roots.
-
Factorization: Method to solve quadratic equations by expressing them as products of linear factors.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The equation x² - 5x + 6 = 0 can be solved by factorization, giving roots x = 2 and x = 3.
-
Using the quadratic formula x = (-b ± √(b² - 4ac)) / 2a helps solve any quadratic equation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For every ax squared plus bx plus c, solve for x with roots you'll see.
📖 Fascinating Stories
-
Imagine a gardener planting two types of flowers in a plot, where the equation helps determine the ideal arrangement for maximum beauty.
🧠 Other Memory Gems
-
D for Discriminant, D for deciding if roots are distinct, equal, or non-existent.
🎯 Super Acronyms
R.E.D - Roots, Equation, Discriminant.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Quadratic Equation
Definition:
An equation of the form ax² + bx + c = 0, where a, b, and c are real numbers, and a ≠ 0.
-
Term: Roots
Definition:
Values of x that satisfy the equation ax² + bx + c = 0.
-
Term: Discriminant
Definition:
The value calculated as b² - 4ac used to determine the nature of the roots of a quadratic equation.
-
Term: Factorization
Definition:
The process of breaking down a quadratic equation into the product of its linear factors.
