Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Tower and Shadow Relationship
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we're discussing how to find the height of a tower using the lengths of its shadow when the sun is at different angles. Can anyone tell me what key relationship we're going to use?

Is it the tangent function?

Exactly! The tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side. Here, the height of the tower is the opposite side. Can someone remind me what the angles of elevation are in our example?

They are 30 degrees and 60 degrees!

Right! Now, let’s break down our first equation. For 60 degrees, we can say tan(60) = height over shadow length. If we call the height 'h' and shadow when sun is at 60 degrees 'x', what does that give us?

It gives us h/x = √3 or h = x√3!

Perfect! Now, let's see how we can apply this with the second angle of elevation.
Setting Up the Second Equation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now, turning to the angle of 30 degrees, we'll create another equation. Can someone tell me how the relationship looks?

For the 30-degree elevation, we have tan(30) which is h divided by the length of the shadow which is '40 + x'.

Correct! What does tan(30) evaluate to?

That would be 1/√3!

So, our equation becomes 1/√3 = h/(40 + x). Now, let's rewrite this in terms of h. What do we get?

h = (40 + x)/√3!

Great work! Now we can substitute our h value back to set up a relationship between x and the constants.
Solving the Equations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Let’s substitute h = x√3 into our other equation. What does that lead us to?

We’ll get √3x = (40 + x)/√3!

Exactly! Multiplying through by √3 gives us 3x = 40 + x. What does this simplify to?

So, we have 3x - x = 40 which means 2x = 40. That gives x = 20!

Excellent work! And with x = 20, can we find the height now?

Yes! h = 20√3, so that’s the height of the tower.

Well done! Let's summarize what we've learned today.
Summary and Key Takeaways
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

So, what are the key points from our lesson today?

We used trigonometric relationships to find the height of a tower based on shadow lengths.

And we made two equations using the tangent function.

Excellent! Always remember that the tangent function relates height to shadow lengths in these types of problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In Example 5, a problem is solved that involves calculating the height of a tower based on the lengths of its shadow when the sun is at different altitudes. Two right triangles are used to set up equations based on the tangent function.
Detailed
Detailed Summary
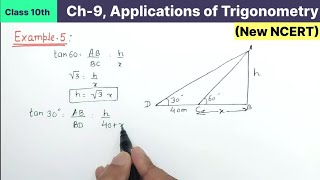
Example 5 deals with a geometric problem surrounding a tower's height and the length of its shadow under two different angles of elevation of the sun (30° and 60°). The solution involves using trigonometric principles, specifically the tangent function, to relate the height of the tower (AB) to the lengths of its shadows (BC and BD) at the specified angles. The relationship established shows that the shadow length at 30° is 40 meters longer than that at 60°, leading to the formulation of two equations based on right triangles formed in the diagram. The mathematical approach culminates in determining that the height of the tower is 20√3 meters.
Youtube Videos



















Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.
Detailed Explanation
In this example, we have a tower whose shadow changes length depending on the position of the sun in the sky. When the sun is at an angle of 60°, the shadow is shorter compared to when the sun is at an angle of 30°. We know that at 30°, the shadow is 40 meters longer than at 60°. The goal is to determine the height of the tower based on these conditions.
Examples & Analogies
Imagine standing next to a streetlamp at different times of the day. In the early morning (like the 30° angle), your shadow is long. But when the sun is directly above at noon (similar to 60°), your shadow is much shorter. The difference in shadow lengths can help you understand how tall the streetlamp is.
Defining Variables
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let AB be h m and BC be x m. According to the question, DB is 40 m longer than BC. So, DB = (40 + x) m.
Detailed Explanation
To solve the problem, we need to define the variables. Let 'h' be the height of the tower (AB) and 'x' be the length of the shadow when the sun's altitude is 60° (BC). The problem states that when the sun's altitude is 30°, the new shadow length (DB) is 40 meters longer than the shadow at 60°, meaning DB = x + 40.
Examples & Analogies
Think of measuring the height of a tree. You decide to use two sticks. One stick (x) represents a shorter shadow when the sun is high, and the other one (DB) represents a longer shadow when the sun is lower. The difference in their lengths helps you understand how much taller the tree is.
Setting Up Right Triangles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, we have two right triangles ABC and ABD. In △ABC, tan 60° = AB/BC or, 3 = h/x (1). In △ABD, tan 30° = AB/DB i.e., 1/√3 = h/(x + 40) (2).
Detailed Explanation
The shadows and the height of the tower create two right triangles. In triangle ABC, the angle of elevation is 60°, and we can express the tangent of that angle as the height of the tower divided by the length of the shadow (tan(60°) = h/x). Similarly, in triangle ABD, at an angle of 30°, we can set up another equation using tangent (tan(30°) = h/(x + 40)). The tangent values correspond to known trigonometric ratios.
Examples & Analogies
If you were to measure how tall a building is using a clinometer, the angles of elevation correspond to your line of sight. The angles give you two different triangles, and by comparing the triangles, you can use trigonometry to find out how tall the building is.
Solving the Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
From (1), we have h = 3x. Putting this value in (2), we get (3x)√3 = x + 40, i.e., 3x = x + 40, i.e., x = 20.
Detailed Explanation
After establishing our equations, we can isolate 'h' in the first equation to find h = 3x. We then substitute this expression for 'h' into the second equation. This allows us to solve for 'x'. After calculations, we find that x equals 20 meters, which represents the shadow's length when the sun's angle is 60°.
Examples & Analogies
Imagine you have a recipe that requires 3 cups of flour for every 1 cup of sugar. If you need to adjust your recipe based on how much sugar you have (similarly to how we adjust our equations), you can find out the exact measurements needed to keep the proportions correct.
Finding the Height of the Tower
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, h = 20√3 [From (1)]. Therefore, the height of the tower is 20√3 m.
Detailed Explanation
Having calculated 'x', we can now substitute it back into our expression for 'h'. We find that the height of the tower is 20 times the square root of 3, which gives us the full height in meters.
Examples & Analogies
If you were to find out how tall a building is through calculations based on different shadows it casts, this final calculation brings you the answer, just like measuring the final height after determining how much material you need for construction.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Height of a Tower: The vertical distance from the base of the tower to its top.
-
Shadow Length: The distance from the base of the object (the tower) to the tip of its shadow.
-
Angles of Elevation: The angles formed with the horizontal line to the line of sight to the top of the tower, measured at 30° and 60° in this case.
-
Trigonometric Functions: Functions such as tangent that relate angles to ratios of sides in triangles.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: If a person stands 10 m away from a tree that is 5 m tall, what is the angle of elevation to the top of the tree?
-
Example 2: A flagpole casts a shadow of length 15 m when the angle of elevation is 45°. What is the height of the flagpole?
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the sun is high and shadows low, the tower's height will surely show.
📖 Fascinating Stories
-
Imagine a brave knight measuring tower heights with a magic shadow stick that grows as the sun bows lower in the sky.
🧠 Other Memory Gems
-
Remember HATS: Height = Adjacent × Tangent of Angle for shadow problems.
🎯 Super Acronyms
SHAD = Shadow Height at Different angles.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Angle of Elevation
Definition:
The angle formed between the horizontal line and the line of sight to an object above the horizontal.
-
Term: Tangent Function
Definition:
A trigonometric function that relates the angle of a right triangle to the ratio of the length of the opposite side to the length of the adjacent side.
-
Term: Right Triangle
Definition:
A triangle where one angle is exactly 90 degrees.
-
Term: Shadow Length
Definition:
The length of the projection of an object, like a tower, cast on the ground due to light, such as sunlight.
-
Term: Trigonometric Relationship
Definition:
Relationships among the angles and sides of triangles.
