Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Sum of Consecutive Odd Numbers
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will explore how perfect cubes can be expressed as the sum of consecutive odd numbers. Can anyone give me an example of a perfect cube?
Eight! That's 2 cubed.
Correct! Eight can also be expressed as 3 + 5. Let's express some more cubes this way!
So 27 is 7 + 9 + 11, right?
Absolutely! And how about we find the sum of odd numbers needed to reach 10Β³ now?
I think it's 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19!
That sums up to 1000!
Great job! Summing consecutive odd numbers gives us an excellent insight into cube numbers.
Cube Differences
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs look at the differences between cubes. For example, what do you think 3Β³ - 2Β³ equals?
That is 27 - 8, which equals 19.
Well done! But we can express that as 1 + 2 Γ 1 Γ 3! Isn't that fascinating?
So we can see some pattern each time we find the difference?
Exactly! The formula we derive helps visualize these calculations better. Letβs try to calculate more together.
Prime Factorization
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, let's cover prime factorization. Remember that each prime factor of a cube appears three times. Who can help me confirm these factors?
For example, 8 is 2 Γ 2 Γ 2, and that proves it's a cube!
Great job! So if I give you the number 27, how would you break that down?
That's 3 Γ 3 Γ 3!
Exactly! Now, letβs check if 64 is a perfect cube using prime factorization.
It is because it's 2 Γ 2 Γ 2 Γ 2 Γ 2 Γ 2, which makes it 4 twos or 2Β³!
Great teamwork, everyone! Prime factorization is a crucial skill.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, students learn how consecutive odd numbers can be summed to yield perfect cubes, discover patterns in cube root calculations, and analyze the structure of prime factorizations leading to cube formation. The unique properties of perfect cubes are reinforced through various exercises and examples.
Detailed
Some Interesting Patterns
This section focuses on intriguing patterns related to numbers, particularly regarding the sums of consecutive odd numbers which equate to perfect cubes.
Key Points:
- Sum of Consecutive Odd Numbers:
- Each perfect cube can be expressed as the sum of an increasing series of consecutive odd numbers. For instance:
- 1 = 1 (1Β³)
- 3 + 5 = 8 (2Β³)
- 7 + 9 + 11 = 27 (3Β³)
- And so forth.
- This pattern prompts exploration into how many consecutive odd numbers sum to other cubes, such as 10Β³.
- Patterns in Cube Differences:
- The differences between cubes have unique representations, for instance:
- 2Β³ - 1Β³ = 1 + 2 Γ 1 Γ 1.
- These differences maintain a consistent structure, suggesting a mathematical relationship valuable for problem-solving and analysis of cubes.
- Prime Factorization of Cubes:
- Each prime factor in a number's cube appears three times in its prime factorization, which can be leveraged to determine whether a number is a perfect cube.
- Practical exercises guided by these observations solidify understanding, including establishing whether given numbers are perfect cubes based on their prime factorizations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Adding Consecutive Odd Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Adding consecutive odd numbers
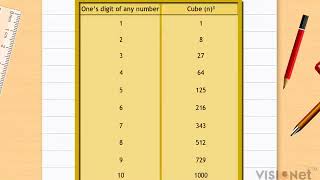
Observe the following pattern of sums of odd numbers.
1 = 1 = 1Β³
3 + 5 = 8 = 2Β³
7 + 9 + 11 = 27 = 3Β³
13 + 15 + 17 + 19 = 64 = 4Β³
21 + 23 + 25 + 27 + 29 = 125 = 5Β³
Is it not interesting? How many consecutive odd numbers will be needed to obtain the sum as 10Β³?
TRY THESE
Express the following numbers as the sum of odd numbers using the above pattern?
(a) 63 (b) 83 (c) 73
Detailed Explanation
In this chunk, we explore the relationship between adding consecutive odd numbers and perfect cubes. The cube of a number n (nΒ³) is represented as the sum of the first n consecutive odd numbers. For instance:
- 1 (1Β³) is obtained from including just the first odd number (1).
- 2Β³ (8) is the sum of the first two odd numbers (3 + 5).
- Similarly, 3Β³ (27) arises from adding 7, 9, and 11.
This pattern continues until 5Β³, representing the sum of 21 through 29. The section challenges you to find how many consecutive odd numbers sum up to 10Β³ (1000), encouraging students to engage with mathematical concepts interactively.
Examples & Analogies
To relate this to a real-life scenario, think of building a structure with blocks. If you add layers of blocks to create a square base, the number of blocks in each layer corresponds to consecutive odd numbers. This method shows how shapes can grow into cubes, similar to how each added layer contributes to completing a larger cube structure.
Difference of Cubes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider the following pattern.
2Β³ β 1Β³ = 1 + 2 Γ 1 Γ 3
3Β³ β 2Β³ = 1 + 3 Γ 2 Γ 3
4Β³ β 3Β³ = 1 + 4 Γ 3 Γ 3
Using the above pattern, find the value of the following.
(i) 7Β³ β 6Β³ (ii) 12Β³ β 11Β³ (iii) 20Β³ β 19Β³ (iv) 51Β³ β 50Β³
Detailed Explanation
This chunk discusses how to find the difference of cubes using a specific pattern. For cubes of succeeding integers, the difference can be expressed in a streamlined equation. For example:
- The difference between 2Β³ and 1Β³ is structured as 2Β³ - 1Β³ = 1 + 2Γ1Γ3 which represents a systematic way to express the result.
This pattern shows that the difference of cubes can become more manageable to calculate.
Examples & Analogies
Imagine a stack of boxes. If you take a smaller box away from a larger one, you can visualize the space left in simpler terms. This visualization symbolizes the pattern found within the differences of cubes methodically, making it easier to understand how larger quantities can be broken down.
Cubes and Their Prime Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Cubes and their prime factors
Consider the following prime factorisation of the numbers and their cubes.
Prime factorisation of a number | Prime factorisation of its cube
4 = 2 Γ 2 | 4Β³ = 64 = 2 Γ 2 Γ 2 Γ 2 Γ 2 Γ 2 = 2Β³ Γ 2Β³
6 = 2 Γ 3 | 6Β³ = 216 = 2 Γ 2 Γ 2 Γ 3 Γ 3 Γ 3 = 2Β³ Γ 3Β³
15 = 3 Γ 5 | 15Β³ = 3375 = 3 Γ 3 Γ 3 Γ 5 Γ 5 Γ 5 = 3Β³ Γ 5Β³
12 = 2 Γ 2 Γ 3 | 12Β³ = 1728 = 2 Γ 2 Γ 2 Γ 2 Γ 2 Γ 2 Γ 3 Γ 3 Γ 3 = 2Β³ Γ 2Β³ Γ 3Β³
Observe that each prime factor of a number appears three times in the prime factorisation of its cube.
Detailed Explanation
In this chunk, we learn how the prime factorization method allows us to understand cubes better. When you prime factorize a number before cubing it, each prime factor multiplies three times. For example, 4 becomes 2Β³ when cubed, showing how each factor contributes to the overall product. This highlights a crucial understanding in the study of mathematics: recognizing structural dependencies through factors.
Examples & Analogies
Think of prime factors as individual building blocks. Each block represents a prime number, and when you stack them up to build a larger cube, you are using each block three times for the volume, much like constructing a building and showing the foundation beneath.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Perfect Cubes: Numbers formed by multiplying an integer by itself three times.
-
Sum Patterns: Perfect cubes can be expressed as the sum of consecutive odd numbers.
-
Prime Factorization: Each prime factor appears three times in a perfect cube.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The number 1 can be expressed as 1Β³, which equals 1.
-
The number 8 can be expressed as a sum of odd numbers: 3 + 5 = 8.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
One, three, five, seven, too; add them up for cubes anew!
π Fascinating Stories
-
Imagine a baker, who counts his cakes in stacks of three. Each stack represents a perfect cube, and he delights in counting them as he adds on croissants using strange odd patterns.
π§ Other Memory Gems
-
SPO# (Sum of Perfect Odd) - Remember to sum to see odd numbers create cubes.
π― Super Acronyms
CUBES - Count Odd Unique Before Every Sum!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Perfect Cube
Definition:
A number that can be expressed as the cube of an integer.
-
Term: Consecutive Odd Numbers
Definition:
A pattern of numbers that are odd and appear one after the other (e.g., 1, 3, 5, 7).
-
Term: Prime Factorization
Definition:
Breaking down a number into its prime components.