Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Polygons
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome everyone! Today, we're going to dive into the fascinating world of polygons. Can someone tell me what a polygon is?
I think a polygon is a shape formed by connecting straight lines.
Yes! And it's a closed shape too.
Great! Exactly. A polygon is a simple closed curve made up only of line segments. Now, can anyone tell me what we might classify polygons as?
Maybe convex and concave?
Exactly! Letβs explore these classifications in detail.
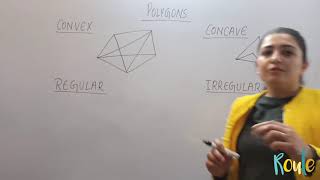
Convex Polygons
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
A convex polygon is one where all line segments connecting any two points within the polygon remain inside it. Can anyone provide an example of a convex polygon?
A square is a convex polygon, right?
That's correct! In a square, all the diagonals and segments connecting points stay inside. Also, all the angles in a convex polygon are less than 180Β°. Now, what about concave polygons?
I think a concave polygon has at least one angle greater than 180Β°.
Exactly! Let's break that down further.
Concave Polygons
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Concave polygons behave differently. Can anyone summarize how they are defined?
A concave polygon has at least one diagonal that extends outside the shape.
Correct! This property is key to identifying concave polygons. When we connect some vertices, we might end up cutting through the exterior space. Can someone give an example of a concave polygon?
Like a star shape?
Absolutely! The star has concave sections, making it a great example. Let's remember: convex means all parts are within, while concave has some parts that extend outward.
Review and Application
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To wrap up, who can tell me the main differences between convex and concave polygons?
In convex polygons, all diagonals are inside, while in concave polygons, at least one diagonal is outside.
And all angles in a convex polygon are less than 180Β°!
Excellent! Remember these distinctions, as they will help us understand more complex shapes later on. Now, for an exercise, can anyone give me two sketches, one of a convex and one of a concave polygon to illustrate these!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In Section 3.1.1, we explore polygons categorized as either convex or concave. Convex polygons have diagonals that lie entirely within their interior, while concave polygons have at least one diagonal that extends outside of them. The importance of understanding these distinctions is emphasized in the context of further studies in polygons.
Detailed
Convex and Concave Polygons
Polygons are defined as simple closed curves made up of line segments, and they can be classified into two main categories: convex and concave.
Convex Polygons
- Definition: A polygon is considered convex if all line segments connecting any two points within the polygon remain completely inside it. Consequently, none of the diagonals (lines connecting non-adjacent vertices) extend outside the polygon itself.
- Characteristics:
- All interior angles are less than 180Β°.
- Any diagonal drawn lies entirely inside the polygon.
Concave Polygons
- Definition: A polygon is convex if at least one diagonal lies outside the polygon. This means that when connecting some vertices, the resulting line segments may extend into the exterior space.
- Characteristics:
- At least one interior angle is greater than 180Β°.
- Some diagonals will cross the boundary of the polygon.
Importance
This distinction between convex and concave polygons is crucial for understanding more complex geometric concepts and properties, particularly in later sections that deal with regular and irregular polygons.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Polygons
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A simple closed curve made up of only line segments is called a polygon.
Detailed Explanation
A polygon is a geometric shape formed by connecting a sequence of points, known as vertices, with straight line segments. The line segments are called sides, and the vertices are the corners of the polygon. When the shape is closed, meaning all the sides connect back to the starting point without any gaps, it's defined as a simple closed curve. Polygons can have different numbers of sides, such as triangles (3 sides), quadrilaterals (4 sides), and so on.
Examples & Analogies
Imagine a shape you might see drawn on a paper, like a drawing of a house. The outlines of the house that connect the corners are polygons. The four walls together with the roof create a closed shape and represent a polygon.
Types of Polygons: Convex vs. Concave
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Polygons that are convex have no portions of their diagonals in their exteriors or any line segment joining any two different points in the interior of the polygon lies wholly in the interior of it. This is not true with concave polygons.
Detailed Explanation
A convex polygon is one where, when you draw a line between any two points within the shape, the line remains inside the polygon. No part of the shape will 'cave in' towards the inside. In contrast, a concave polygon has at least one internal angle greater than 180 degrees, meaning that when you connect two points within the shape, the line may pass outside the polygon's edges.
Examples & Analogies
Think about a tent. If all the edges of the tent are stretched outward, it forms a convex shape. However, if part of the tent is pushed inward, creating a 'cave,' it represents a concave polygon. The convex shape keeps everything inside while the concave one has parts where the edges bend inward.
Visualizing Convex and Concave Polygons
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Study the figures given. Then try to describe in your own words what we mean by a convex polygon and what we mean by a concave polygon. Give two rough sketches of each kind.
Detailed Explanation
To understand the differences between convex and concave polygons visually, look at illustrations or create sketches yourself. A convex polygon might look like a regular hexagon where every angle is less than 180 degrees. Meanwhile, a concave polygon could be a star shape or any figure that has at least one inward dent. Describing these shapes helps solidify your understanding of polygons in two dimensions.
Examples & Analogies
Imagine the shapes of various objects. A bookshelf is a good example of a convex shape: its front is entirely outward. Now, think about a wedge of cheese, where one side is pushed inβthat creates a concave shape. Visualizing everyday objects can deepen your grasp of these concepts.
Focus on Convex Polygons
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In our work in this class, we will be dealing with convex polygons only.
Detailed Explanation
In this lesson, the focus will be solely on convex polygons because they are generally simpler to work with for calculations involving angles, perimeter, and area. Convex polygons do not present complications like concave polygons, where lines might crisscross outside the shape, making calculations more complex.
Examples & Analogies
When building models or structures, architects often prefer convex shapes because they offer better stability and are easier to manage. For example, when designing parks, which often have paths that are simple to follow and enclosed spaces, convex shapes like circles or ovals are favored.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Polygon: A closed figure formed by connecting line segments.
-
Convex Polygon: No diagonals extend outside; all angles are less than 180Β°.
-
Concave Polygon: At least one diagonal extends outside; at least one angle is greater than 180Β°.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A square and a triangle are examples of convex polygons.
-
A star shape or an arrowhead are examples of concave polygons.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In a convex shape, all points stay tight, / Concave shapes stretch, a broader sight.
π Fascinating Stories
-
Once in Geometry Land, there lived two families: the Convexes, always staying safe inside their homes, and the Concaves, who loved to extend their arms outside, reaching for the sky!
π§ Other Memory Gems
-
C for Convex means 'C for Closed' β all angles are less than 180Β°, while C for Concave means 'C for Cut-out' β where at least one angle pushes out!
π― Super Acronyms
Remember C.C. for Concave - where a path is Cut out, versus V.V. for Convex - where it's all Within!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Polygon
Definition:
A simple closed curve composed of line segments.
-
Term: Convex Polygon
Definition:
A polygon where all diagonals lie entirely inside and all interior angles are less than 180Β°.
-
Term: Concave Polygon
Definition:
A polygon where at least one diagonal lies outside and at least one interior angle is greater than 180Β°.