7.2 - Congruence of Triangles

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Introduction to Congruence

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we'll learn about congruence, particularly in triangles. Can anyone tell me what congruence means?

Student 1
Student 1

Isn't it when two shapes are the same size and shape?

Teacher
Teacher

Exactly! We call figures that are the same in shape and size 'congruent'. For example, two triangles are congruent if their corresponding sides and angles match.

Student 2
Student 2

So, if they fit perfectly on top of each other, they are congruent?

Teacher
Teacher

That's right! This perfect overlay is important in geometrical proofs and applications.

Criteria for Congruence

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let’s dive deeper. We have several criteria to check if triangles are congruent. Can someone name one?

Student 3
Student 3

Is it the SAS criterion?

Teacher
Teacher

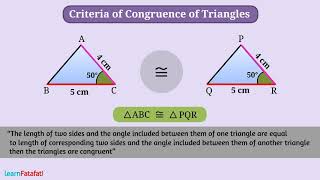
Correct! The SAS criterion states that if two sides and the angle between them in one triangle are equal to those in another, then the triangles are congruent. Can anyone else mention another criterion?

Student 4
Student 4

There's also the ASA criterion, right?

Teacher
Teacher

Absolutely! The ASA states that if two angles and the included side are equal in two triangles, they are congruent. Remember to consistently denote corresponding parts when discussing congruence.

Examples and Applications

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let’s consider real-life examples showcasing congruence. Why is understanding congruence important? Any thoughts?

Student 1
Student 1

It helps in construction and manufacturing to ensure that parts fit together perfectly.

Teacher
Teacher

Great point! For instance, the parts of a car engine must be congruent for everything to fit correctly. Can anyone think of another example?

Student 2
Student 2

In art or crafting, we might need pieces to be congruent for things to look uniform.

Teacher
Teacher

Exactly! Understanding congruence is vital in many fields. Let's summarize our learning today.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section elaborates on the concept of congruence in triangles, discussing how triangles are congruent when their corresponding sides and angles are equal.

Standard

This section introduces the definition of congruence, outlines several examples of congruent figures, and explains the principles behind the congruence of triangles. It covers the criteria for triangle congruence, such as the SAS, ASA, and SSS rules, emphasizing the significance of corresponding parts in congruent triangles.

Detailed

Congruence of Triangles

In this section, we explore the concept of congruence, primarily focusing on triangles. Congruent figures are those that have identical shapes and sizes. The section highlights that two triangles are congruent if their corresponding sides and angles are equal. Various criteria for triangle congruence are introduced, including:

  1. SAS (Side-Angle-Side) Theorem: Two triangles are congruent if two sides and the angle between them are equal.
  2. ASA (Angle-Side-Angle) Theorem: Two triangles are congruent if two angles and the side between them are equal.
  3. SSS (Side-Side-Side) Theorem: Two triangles are congruent if all three sides of one triangle are equal to all three sides of another triangle.
  4. AAS (Angle-Angle-Side) Theorem: Two triangles are congruent if two angles and a non-included side are equal.
  5. RHS (Right angle-Hypotenuse-Side) Theorem: If in two right triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.

The concept of congruence is essential in applications such as manufacturing, where identical pieces need to fit together perfectly. Additionally, the section emphasizes the importance of consistent notation when denoting congruent triangles, which includes proper correspondence of their vertices. The section concludes with exercises that reinforce the understanding of triangle congruence through practical examples.

Youtube Videos

GCSE Maths - Congruent Triangle Rules
GCSE Maths - Congruent Triangle Rules
Triangles Class 9 in One Shot 🔥 | Class 9 Maths Chapter 7 Complete Lecture | Shobhit Nirwan
Triangles Class 9 in One Shot 🔥 | Class 9 Maths Chapter 7 Complete Lecture | Shobhit Nirwan
Criteria of Congruence of Triangles
Criteria of Congruence of Triangles
Class 9 Maths Triangles| Introduction & All Basic Concepts in Easy way | Congruent Triangles | CBSE
Class 9 Maths Triangles| Introduction & All Basic Concepts in Easy way | Congruent Triangles | CBSE
📐 type of triangle 📐
📐 type of triangle 📐
Congruent triangles vs Similar triangles
Congruent triangles vs Similar triangles
Triangles L1 | Congruence of Triangles | CBSE Class 9 | Maths Chapter 7 | NCERT Solutions (2019)
Triangles L1 | Congruence of Triangles | CBSE Class 9 | Maths Chapter 7 | NCERT Solutions (2019)
maths project work.... congruence of triangles #triangle #shorts #subscribe
maths project work.... congruence of triangles #triangle #shorts #subscribe
Find angle of triangle
Find angle of triangle
Quadrilateral class 9 problem
Quadrilateral class 9 problem

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Introduction to Congruence

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

You must have observed that two copies of your photographs of the same size are identical. Similarly, two bangles of the same size, two ATM cards issued by the same bank are identical. You may recall that on placing a one rupee coin on another minted in the same year, they cover each other completely. Do you remember what such figures are called? Indeed they are called congruent figures ('congruent' means equal in all respects or figures whose shapes and sizes are both the same).

Detailed Explanation

This chunk introduces the concept of congruence, highlighting that congruent figures are identical in both shape and size. Examples such as photographs, bangles, and coins illustrate how everyday objects can be congruent. When we say two figures are congruent, it implies that they can perfectly overlap each other without any gaps or mismatches.

Examples & Analogies

Think of two identical puzzle pieces. If you put one on top of the other, they fit perfectly. This is similar to how congruent figures work; they match exactly in shape and size.

Examples of Congruent Figures

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Now, draw two circles of the same radius and place one on the other. What do you observe? They cover each other completely and we call them congruent circles. Repeat this activity by placing one square on the other with sides of the same measure or by placing two equilateral triangles of equal sides on each other. You will observe that the squares are congruent to each other and so are the equilateral triangles.

Detailed Explanation

This chunk provides practical activities using circles, squares, and equilateral triangles to demonstrate congruence visibly. By placing the same shapes on top of each other, students can physically see that they align perfectly, reinforcing the definition of congruence in an engaging manner.

Examples & Analogies

Imagine stacking two identical plates one on top of the other. If they are the same size and shape, they will match perfectly, which is the essence of congruent figures.

Importance of Congruence

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

You may wonder why we are studying congruence. You all must have seen the ice tray in your refrigerator. Observe that the moulds for making ice are all congruent. The cast used for moulding in the tray also has congruent depressions... So, you can find numerous examples where congruence of objects is applied in daily life situations.

Detailed Explanation

This chunk discusses real-world significance of understanding congruence. It emphasizes that many manufacturing processes, like creating ice trays, rely on congruent shapes to ensure all produced items are identical. This has practical applications in various fields including engineering, architecture, and even kitchen gadgets.

Examples & Analogies

Think about cookie cutters - they are made to cut dough into congruent shapes. When you use the same cookie cutter, every cookie comes out looking exactly the same, which shows how congruence is essential in cooking and baking.

Identifying Congruent Triangles

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Now, which of the triangles given below are congruent to triangle ABC? Cut out each of these triangles from Fig. 7.4 (ii) to (v) and turn them around and try to cover ∆ ABC. Observe that triangles in Fig. 7.4 (ii), (iii), and (iv) are congruent to ∆ ABC while ∆ TSU of Fig 7.4 (v) is not congruent to ∆ ABC.

Detailed Explanation

Here, students are engaged in a hands-on activity to find congruent triangles among different figures. By physically manipulating the triangles, they learn how congruence depends on the equality of their corresponding sides and angles, reinforcing the concept through practice.

Examples & Analogies

Consider matching socks – if you have a pair of socks, they are congruent because they are identical. If one sock is different in color or size, it no longer matches, just like how only certain triangles match in shape and size.

Correspondence in Congruence

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

If ∆ PQR is congruent to ∆ ABC, we write ∆ PQR ≅ ∆ ABC. Notice that when ∆ PQR ≅ ∆ ABC, then sides of ∆ PQR fall on corresponding equal sides of ∆ ABC and so is the case for the angles. That is, PQ covers AB, QR covers BC, and RP covers CA; ∠ P covers ∠ A, ∠ Q covers ∠ B, and ∠ R covers ∠ C.

Detailed Explanation

This chunk emphasizes the importance of noting the correspondence between triangles when discussing congruence. It explains the notation used to signify that two triangles are congruent and how we match their corresponding parts, which is crucial for understanding the true definition of congruence.

Examples & Analogies

Think of two identical toy cars. If you name one car as 'A' and the other as 'P', you could say 'Car P is identical to Car A', showing how the names correspond to their matching parts, just like in congruent triangles.

Correctly Writing Congruence

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

It is necessary to write the correspondence of vertices correctly for writing of congruence of triangles in symbolic form. Note that in congruent triangles corresponding parts are equal and we write in short ‘CPCT’ for corresponding parts of congruent triangles.

Detailed Explanation

This chunk presents the importance of writing congruence symbols correctly and understanding that when two triangles are established as congruent, all their corresponding parts (sides and angles) are equal. This consistency in notation helps avoid confusion in mathematical communication.

Examples & Analogies

Consider two identical chairs in a room. If we label one as Chair A and the other as Chair B, we can say they are congruent. Whenever we refer to Chair A, we mean Chair B is the same – this correspondence is vital just like in the notation of congruent triangles.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Congruent Figures: Figures that have identical shapes and sizes.

  • Criteria for Congruence: Rules that help determine whether two triangles are congruent, including SAS, ASA, AAS, SSS, and RHS.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • Two triangles with both pairs of corresponding sides and angles equal are congruent by the criteria of SAS.

  • If two triangles share a side and have two equal angles adjacent to that side, they are congruent by the ASA criterion.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • If sides and an angle are the same, then congruence is the name of the game.

📖 Fascinating Stories

  • Imagine two friends, Amy and Sally, who both have perfectly identical bags. They use them for their identical laptops. Just like their bags, congruent triangles are identical in size and shape.

🧠 Other Memory Gems

  • For triangle congruence remember: SAS, ASA, AAS, SSS. Just think 'Silly Animals Sing Sweetly.'

🎯 Super Acronyms

Use the acronym 'CATS' to remember congruence rules

  • Corresponding parts
  • All sides
  • Triangles
  • Same angles.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Congruence

    Definition:

    The property of figures having the same shape and size.

  • Term: SAS Criterion

    Definition:

    A rule stating that two triangles are congruent if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle.

  • Term: ASA Criterion

    Definition:

    A rule that states that two triangles are congruent if two angles and the side between them are equal in both triangles.

  • Term: SSS Criterion

    Definition:

    A statement that if three sides of one triangle are equal to three sides of another triangle, the two triangles are congruent.

  • Term: AAS Criterion

    Definition:

    A theorem stating that if two angles and a non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, the triangles are congruent.

  • Term: RHS Criterion

    Definition:

    A rule applying specifically to right triangles; states that if the hypotenuse and one side are equal, the triangles are congruent.

  • Term: CPCT

    Definition:

    Corresponding Parts of Congruent Triangles, meaning that the parts of congruent triangles are equal.