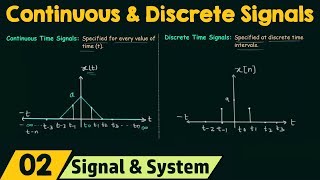
Introduction to Discrete-Time Signals
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Discrete-Time Signals
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are discussing discrete-time signals. Can anyone tell me what a discrete-time signal is?

Isn't it a signal that is only defined at certain intervals?

Exactly! Discrete-time signals are defined at discrete intervals, which means they are sampled from continuous signals. We represent them as sequences like x[n]. What does the ‘n’ in x[n] represent?

Isn't it the integer index that tells us the position in the sequence?

Correct! The index n helps us identify specific samples in the sequence. Remember, DSP often involves operating on these sequences. Let's now think about how we analyze these signals.
Operations on Discrete-Time Signals
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand discrete-time signals, let’s explore two important operations: convolution and correlation. Can someone tell me the purpose of convolution?

Isn't it used to find the output of a system based on an input signal and the system's impulse response?

Absolutely! Convolution combines the input signal with the system's impulse response. You can think of it as how an input signal is modified by a system characterized by its response. How do you think we represent this mathematically?

Isn't it like y[n] equals the sum over x[k] times h[n-k]?

Great job! Remember to visualize the convolution process as sliding the impulse response over the input signal. Now let's compare that with correlation. What differentiates correlation from convolution?
Applications and Importance of Discrete-Time Signals
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Applications of these operations are vast. Can anyone think of where we might use convolution in a practical application?

Maybe in digital filtering?

Exactly! Convolution is central to implementing digital filters, which can remove unwanted frequencies from signals. And what about correlation? Where might that be useful?

I think it could be used in pattern matching, like in audio recognition?

Absolutely! Correlation is key in detecting and matching signals. It highlights the significance of understanding these concepts for anyone working in DSP. We'll wrap up with one last thought: understanding these operations can help design effective systems. Any final questions?
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In the realm of Digital Signal Processing, discrete-time signals are sequences derived from continuous signals, allowing for their analysis and manipulation. This section explores fundamental concepts such as discrete-time signal definition, sequence representation, and vital operations including convolution and correlation which facilitate understanding the interactions within systems.
Detailed
Discrete-time signals represent quantities sampled from continuous-time signals, forming a fundamental concept in Digital Signal Processing (DSP). These signals are sequences indexed by integers, enabling various operations that reveal how signals interact within systems. This section elaborates on key concepts like the definition and sequence representation of discrete-time signals, leading into crucial operations such as convolution and correlation that underpin the interactions of signals with systems and illustrate how to manipulate and analyze these signals effectively.
Youtube Videos

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Discrete-Time Signals
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Discrete-time signals are sequences of data or values indexed by integers, typically representing quantities sampled from continuous-time signals.
Detailed Explanation
Discrete-time signals are a way to represent signals that change over time by taking samples at specific intervals. Unlike continuous-time signals, which can take any value at any moment, discrete-time signals consist of values that are defined for specific, separated points in time. For example, if we have a continuous sound wave, we can choose to sample it every 0.1 seconds; the captured samples at these intervals form a discrete-time signal.
Examples & Analogies
Think of it like taking photos at a parade. If you take a picture every few seconds, you create a series of snapshots (discrete-time signals) that capture individual moments in the parade. However, if you were able to record the entire parade continuously, that would be analogous to a continuous-time signal.
Importance in Digital Signal Processing
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
These signals are a fundamental concept in Digital Signal Processing (DSP), where the continuous data is represented and processed in a discrete format.
Detailed Explanation
In Digital Signal Processing, discrete-time signals are vital because computers and digital devices handle and process data in discrete formats. Instead of dealing directly with continuous signals, DSP works with sequences of numbers that represent sampled values of these signals. This processing is essential for tasks such as audio and video compression, filtering, and more.
Examples & Analogies
Imagine you’re digitizing a vinyl record. You can’t play the record continuously through a computer; instead, you sample the music at fixed intervals (like every 0.01 seconds) to create a digital file that captures the essence of the music without needing to handle the continuous waveform directly.
Analyzing Discrete-Time Signals
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Discrete-time signals can be analyzed and manipulated using various operations such as convolution and correlation, which are key to understanding how signals interact with systems.
Detailed Explanation
Analyzing discrete-time signals involves various mathematical operations that allow us to understand their properties and how they behave when processed by systems. Convolution and correlation are two such operations. Convolution helps determine the output of a system when a specific input is provided, while correlation helps us understand the similarity between two signals. Both play crucial roles in applied digital signal processing.
Examples & Analogies
Think of convolution like blending different flavors to create a new recipe, where you mix ingredients (signals) to understand how they will come together. Correlation, on the other hand, is like comparing two recipes to see if they are similar in taste; you assess how similar two flavors are as you gradually include different ingredients.
Key Concepts in Discrete-Time Signals
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Key Concepts:
● Discrete-Time Signal: A signal defined only at discrete intervals, typically obtained by sampling a continuous signal.
● Sequence Representation: Discrete-time signals are typically represented as sequences x[n], where n is an integer index.
Detailed Explanation
The key concepts in discrete-time signals include the definition itself, which specifies that they are only defined at specific intervals, unlike continuous signals that can take values at any moment. Furthermore, these signals are often represented using sequences indexed by integers, symbolized as x[n]. Here, 'n' indicates the sample number or time step, giving us a way to reference each value easily.
Examples & Analogies
You can think of a discrete-time signal as a train schedule; each train departs (a specific signal value) only at fixed intervals (discrete time). The schedule (sequence x[n]) shows you when each train (signal) leaves, but there's no information about what happens in between train departures.
Key Concepts
-
Discrete-Time Signal: A signal defined only at specific intervals, often derived through sampling.
-
Convolution: A key operation to analyze signal behavior in systems, determining output based on an input signal and the system's impulse response.
-
Correlation: A method to assess the similarity between two signals, significant for applications in detecting patterns.
Examples & Applications
For discrete-time signals, an example could be x[n]={1, 2, 3}, representing sampled values.
An example of convolution might involve calculating the output for x[n]={1, 2, 3} and h[n]={0.5, 1, 0.5}, resulting in a new sequence.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To understand signals that jump and play, discrete-time samples are here to stay.
Stories
Imagine a baker who prepares cupcakes only at specific hours; just like sampling a signal at certain points creates discrete-time signals.
Memory Tools
C: Combine - O: Output - N: Needs - V: Values - O: Of - L: Linear - U: Underlying - T: Transformation - I: Interactions - O: Overlap - N: Necessary
Acronyms
DSS (Discrete-time Signal Sampling) for SOS
Stop
Obtain
Slide - for convolution calculations.
Flash Cards
Glossary
- DiscreteTime Signal
A signal defined only at discrete intervals, obtained by sampling a continuous signal.
- Sequence Representation
Discrete-time signals are represented as sequences, typically denoted by x[n], where n is an integer index.
- Convolution
A mathematical operation that combines two signals to determine the output of a system based on its input and impulse response.
- Correlation
A measure of similarity between two signals as a function of the time-lag applied to one of them.
Reference links
Supplementary resources to enhance your learning experience.
