Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the DFT and Its Mathematical Formula
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into the Discrete Fourier Transform, or DFT. It is essential in analyzing discrete-time signals. Can anyone tell me why it's important to analyze signals in the frequency domain?
I think it's because it helps us to understand what frequencies are present in a signal?
Exactly! The DFT gives us the frequency content of a signal, helping us identify these frequencies. Letβs look at the mathematical formula. The DFT is defined as: X[k] = β(from n=0 to N-1) x[n] e^{-j2Οkn/N}. What does each part represent?
x[n] is the discrete-time signal we start with, and X[k] is the output in the frequency domain, right?
That's correct! And N represents the total number of samples in the signal. This formula effectively decomposes our signal into its frequency components! Can anyone summarize the role of k and N in this equation?
k tells us which frequency bin we're looking at, and N is how many samples we have!
Great job summarizing! So, X[k] gives us insights into the frequency content of our signal from those samples.
The Role of FFT in DFT Computation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've established what the DFT is, letβs discuss the Fast Fourier Transform, or FFT. Why do you think the FFT is significant in relation to the DFT?
Is it because calculating the DFT directly can take a lot of time if there are many samples?
Exactly! Calculating the DFT directly requires O(N^2) computations, which can be quite intensive. The FFT, however, reduces that to O(N log N) computations. Can anyone explain why this is beneficial?
It makes processing longer signals possible in real-time applications since it's much faster!
Correct! The FFT allows for practical applications in areas like audio processing and real-time communications. Could you give an example of one such application?
I think in audio processing, we use FFT to analyze sound wavelengths and frequencies efficiently when we process music!
Excellent point! FFT is vital in breaking down audio signals to manipulate them effectively.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section outlines the Discrete Fourier Transform (DFT), detailing its mathematical formulation and application in analyzing discrete-time signals. It highlights how the DFT computes the frequency content of finite-length signals and introduces the Fast Fourier Transform (FFT) algorithm as an efficient implementation method.
Detailed
Detailed Summary
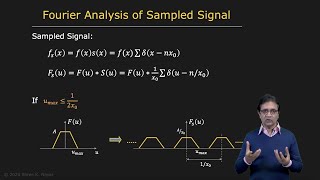
The Discrete Fourier Transform (DFT) is a crucial tool in digital signal processing for analyzing discrete-time signals within the frequency domain. The DFT converts a finite sequence of equally spaced samples of a signal into its frequency components, allowing for the extraction of significant information regarding its spectral content.
Mathematical Definition
The DFT of a discrete-time signal is defined by the following equation:
$$X[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi \frac{k n}{N}}$$
Where:
- x[n] is the input discrete-time signal,
- X[k] is the DFT output,
- N is the total number of samples,
- k is the index representing the frequency bins.
This transformation allows the signal to be represented as a sum of complex exponentials, aiding in the analysis of its frequency characteristics.
Fast Fourier Transform (FFT)
Due to the computational complexity of the DFT, the Fast Fourier Transform (FFT) algorithm is often employed to calculate the DFT efficiently. FFT reduces the number of computations needed, making it feasible to analyze longer signals in practical applications.
The importance of the DFT lies in its ability to break down discrete-time signals into their constituent frequencies, which is vital for tasks like filtering, compression, and feature extraction in various applications such as audio processing, communication systems, and more.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of the DFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Discrete Fourier Transform (DFT) is used to analyze discrete-time signals in the frequency domain. The DFT is defined as:
X[k]=βn=0Nβ1x[n]eβj2ΟknN
Where:
β x[n] is the discrete-time signal.
β X[k] is the DFT of the signal.
β N is the number of samples.
β k is the frequency index.
Detailed Explanation
The Discrete Fourier Transform (DFT) takes a finite number of sample points from a discrete-time signal and transforms them into a representation in the frequency domain. Essentially, it converts time-based data into frequency-based data, allowing us to see how much of each frequency is present in the original signal. The DFT formula sums contributions from each sample multiplied by a complex exponent, which helps to isolate the frequency components based on the index k.
Examples & Analogies
Think of the DFT like a chef analyzing flavors in a dish. Each sample from the signal is like a different ingredient in that dish. When the chef tastes the dish (calculates the DFT), they can identify how strong each flavor (frequency) is, allowing them to understand and modify the dish (signal) for a better outcome.
Components of the DFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β x[n] is the discrete-time signal.
β X[k] is the DFT of the signal.
β N is the number of samples.
β k is the frequency index.
Detailed Explanation
In analyzing the DFT, we need to understand its components:
- x[n] represents the original signal in discrete form, such as samples of audio or data collected at regular intervals.
- X[k] is the resulting DFT, which shows how much of each frequency (represented by index k) is present in the original signal.
- N indicates how many samples we have, which can affect the resolution of our frequency analysis.
- k is the index that helps us identify which frequency we are looking at in the transformed version.
Examples & Analogies
Imagine a musician recording a piece of music with 100 notes (samples). Here, the musician's recorded notes are x[n]. After performing a DFT, the musician can see how much of each musical note (frequency) is in the piece, represented by X[k]. The number of different notes in the piece (N) helps determine the richness of the arrangement, while k helps the musician pinpoint each specific note in the final composition.
Purpose of the DFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The DFT is used to compute the frequency content of a finite-length signal and is implemented efficiently using the Fast Fourier Transform (FFT) algorithm.
Detailed Explanation
The main purpose of the DFT is to analyze the frequency components of discrete signals, enabling us to determine which frequencies are present and their strengths. Because signals in the real world are often long and complex, the DFT can be computationally intensive. To address this, algorithms like the Fast Fourier Transform (FFT) are used, which compute the DFT much more quickly without sacrificing accuracy, making it possible to perform frequency analysis in real-time applications.
Examples & Analogies
Consider a detective analyzing different sound waves that enter a crowded room. The DFT is like a set of tools that helps the detective to filter through the noise and identify specific sounds (frequencies) that are important. The FFT is even like an advanced audio editor that speeds up this filtering process, allowing the detective to listen to the key sounds more efficiently, helping them solve the mystery faster.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Discrete Fourier Transform: Converts a sequence of samples into frequency components.
-
Fast Fourier Transform: An efficient algorithm for computing the DFT.
-
Frequency Domain: Representation of signals in terms of their frequency components.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A musician uses the DFT to analyze their audio track to identify predominant frequencies present in the music.
-
An engineer applies the FFT in real-time communication systems to rapidly compress and process signals for transmission.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In digital signals we trust, the DFT is a must!
π Fascinating Stories
-
Imagine a musician tuning their guitar. They use the DFT to identify which strings are out of tune, focusing on distinct frequencies to make the perfect sound.
π§ Other Memory Gems
-
Remember DFT as 'Discrete Figuring in Time.' It helps pull frequency secrets from time samples!
π― Super Acronyms
FFT stands for 'Faster Frequency Transform,' emphasizing speed in signal processing.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Discrete Fourier Transform (DFT)
Definition:
A mathematical transform used to convert a finite sequence of equally spaced samples of a signal into its frequency components.
-
Term: Fast Fourier Transform (FFT)
Definition:
An efficient algorithm for computing the Discrete Fourier Transform, reducing the computational complexity.
-
Term: Frequency Domain
Definition:
A representation of a signal or function in terms of the frequencies involved in it.
-
Term: Complex Exponential
Definition:
A function of the form e^{jΞΈ}, which can be used to represent sinusoidal signals in a convenient mathematical format.