Transport of Pollutants - Introduction
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Pollutant Transport
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore how pollutants are transported in various environments. What do you think happens to the concentration of a pollutant as it moves from its source to a receptor?

I think it might change as it travels, but I'm not sure how.

Great observation! Yes, the concentration can indeed change. Our goal is to model this transport through mathematical expressions. Remember, concentration is fundamental for understanding exposure to pollutants.

How do we measure this concentration over time?

That leads us to measurement techniques adapted for monitoring pollutant transport! Let’s dive deeper into mass balance equations.
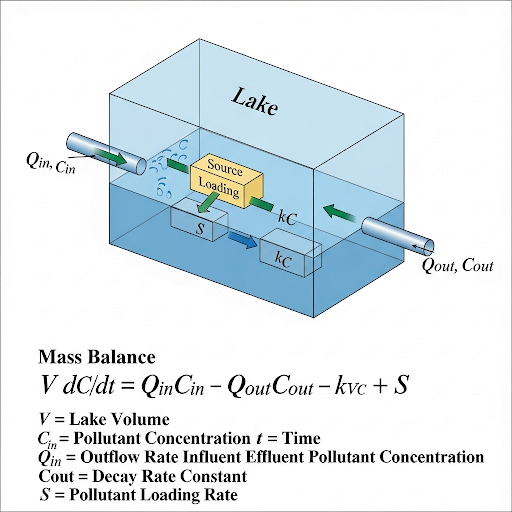
Mass Balance Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's review the mass balance equation. Can anyone tell me how it's formulated?

Is it related to the rate of generation and loss of a pollutant?

Exactly! It's written as \( \frac{dM_A}{dt} = \text{Rate In} - \text{Rate Out} \). This equation helps us track how the concentration changes in a system!

What does it mean if we have a positive rate?

A positive rate indicates accumulation of the pollutant. Remember, understanding the dynamics of mass balance is critical for effective environmental management.
Application to a Lake Example
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's visualize this with a lake. If we have a chemical uniformly mixed in it, what would affect the concentration?

Adding more pollutants or losing some, like through evaporation?

Exactly! The concentration only changes if there’s a net addition or loss. This is a crucial point in our mass balance analysis!

So, what do we do if we want to estimate how concentration changes over time?

We can manipulate our mass balance equations accordingly to incorporate rates of generation and loss. Let’s practice modeling those scenarios!
Box Model Concept
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

In complex flowing systems, we use a box model. Can anyone explain what a box model represents?

I think it’s a way to break the system into smaller parts to manage calculations?

Precisely! It allows us to treat each section as a well-mixed system, simplifying the calculations significantly. Let's see how this plays out in a river.

But what happens if the river is not well-mixed?

Excellent question! While we often assume well-mixed conditions for simplicity, real-world rivers can have gradients and flow complexities. It emphasizes the importance of understanding the system dynamics!
Challenges in Predicting Concentration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

As we wrap up, let’s discuss the challenges in predicting pollutant concentrations in rivers. What difficulties might arise?

Different tributaries or inflows could alter concentrations quickly.

Spot on! Additionally, varying terrains and backflow complicate modeling efforts. It’s crucial to take real-time measurements to refine our models.

So, keeping track of all these factors is important for accurate assessments?

Absolutely! Understanding each contributing factor enables us to create more effective and precise environmental control strategies.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the focus is on understanding how pollutants move from sources to receptors, emphasizing the significance of estimating concentration levels and employing mathematical models to validate these estimations. A special case is presented by introducing a lake as a fixed system for exploring the effects of mass balance on chemical concentration.
Detailed
Detailed Summary
This section delves into the fundamental principles governing the transport of pollutants in the environment. The primary objective is to estimate the concentration of pollutants (denoted as ρ) in scenarios ranging from static bodies of water, like lakes, to dynamic systems, such as rivers. The concept of concentration is crucial since it directly correlates with potential exposure to pollutants.
The section begins by introducing a simplified example involving a lake where a chemical of certain concentration is thoroughly mixed. In this scenario, the concentration remains uniform until external factors, such as addition or loss of the chemical, come into play. This leads to the importance of applying mass balance equations to assess how these changes influence the concentration over time.
The mass balance equation (
$$ \frac{dM_A}{dt} = \text{Rate In} - \text{Rate Out} $$
) outlines how the accumulation of pollutants in a system is affected by generation and loss rates. The discussion also highlights conditions under which a system is considered unsteady-state, where concentration changes over time.
Further, the concept of utilizing a box model is introduced, wherein pollutants in flowing systems, like rivers, are simplified into sections for concentration modeling. The idea of well-mixed compartments makes it easier to analyze the complex dynamics of pollutant transport, although it is noted that real-world scenarios, especially in rivers, can complicate these simplified models due to varying flow conditions and additional tributaries. Finally, a reflection on the applicability of these principles in environmental engineering is offered, stressing the need for robust models to predict and estimate pollutant concentrations reliably.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Objective of Pollutant Transport
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, we move on to the next section, which is on transport of pollutants. Our goal is still what we have been discussing right from the beginning, our objective is to estimate the concentration rho, rho, w any of these in the environment under a wide variety of scenarios. In other words, we are just interested in finding concentration, as concentration is the main quantity that we are interested in terms of exposure.
Detailed Explanation
The objective of studying pollutant transport focuses on understanding and estimating the concentration of pollutants in the environment. Concentration is crucial because it directly relates to human and ecological exposure to harmful substances. By estimating pollutant concentration, we can evaluate potential health risks and make informed decisions about environmental management.
Examples & Analogies
Imagine you are trying to estimate the concentration of sugar in a glass of lemonade. If you know how much sugar you added and the total volume of the lemonade, you can calculate the concentration. Similarly, scientists need to estimate pollutant concentrations in natural water bodies to determine if they are safe for swimming or drinking.
Pollutant Transport Modeling
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
As a pollutant moves from a source to a receptor, what happens to the concentration? Is it change, how does it change? Can we predict it? Can we measure it? So, primarily we are looking at modeling of this pollutant transport mainly and then because we have a model, we must be able to validate that model.
Detailed Explanation
Understanding how pollutant concentrations change as they travel from sources (like factories) to receptors (like people or animals) is vital. This involves creating models to predict these changes, which can account for various environmental factors. The validity of these models is verified through measurements and comparisons with real data, ensuring that predictions are accurate and reliable.
Examples & Analogies
Consider a race car on a track. Engineers use models to predict how fast the car will go at different points based on its engine power and track conditions. Similarly, environmental scientists use models to predict how pollutants will behave in different environmental conditions.
Mass Balance for Pollutants
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When we say it is well mixed, we are obviously assuming that the concentration is uniform. So, if it is well mixed, we will not worry about how it is mixing. Now, if I want to predict, consider this is a fixed volume, which means there is no flow of water inside or outside. If there is a chemical inside, what is likely to happen to the chemical concentration here?
Detailed Explanation
In a well-mixed system like a lake, assuming that pollutants are evenly distributed simplifies calculations. If there is no water entering or leaving the lake, the concentration of any pollutant will only change if it is added or removed (through reactions or evaporation). This concept is known as the mass balance, which involves summing all inputs and outputs to understand changes in concentration.
Examples & Analogies
Think of a sealed jar with a drop of food coloring in water. If you don't shake the jar, the color will eventually disperse evenly throughout. If you add more dye or let some escape (e.g., through evaporation), it will change the concentration in the jar, similar to how pollutants behave in a fixed environment.
Unsteady-State vs. Steady-State Conditions
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is a general equation that can be applied to any system. But we define according to our system as the rate of accumulation in the lake. The rate of accumulation exists only when the system is in unsteady state. What we mean by unsteady state is, the concentration is changing.
Detailed Explanation
In an unsteady state, the concentration of pollutants changes over time. For example, if more pollutants enter the lake than leave, the concentration of pollutants will rise. Conversely, in a steady-state, the concentration remains constant over time, which occurs when the rate of inputs equals the rate of outputs. Understanding which state a system is in helps predict how concentrations will behave.
Examples & Analogies
Imagine a bathtub filling with water but having a drain. If the water flows in faster than it drains out, the water level (or pollutant concentration) rises—this is unsteady state. If the inflow and outflow are balanced, the water level remains the same, indicating a steady state.
Rate of Generation and Loss Mechanisms
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, if you know what is the rate at which loss or generation is occurring in that particular process, you have to put that equation here. So, it could be anything say, rate of generation is reaction and loss is evaporation.
Detailed Explanation
The rate at which pollutants are generated (through chemical reactions) or lost (through processes like evaporation or sedimentation) significantly impacts the overall concentration. Understanding these rates is essential for creating accurate models and predictions about how pollutants behave in the environment.
Examples & Analogies
Imagine cooking a pot of pasta. If you keep adding salt (generating concentration) but also have a little boil-over (losing concentration), you need to balance the salt addition and overflow to maintain the flavor. Similarly, environmental scientists balance pollutant generation and loss to gauge overall concentrations.
Key Concepts
-
Pollutant Transport: The movement of harmful substances from their source to receptors.
-
Concentration: An essential quantity in assessing exposure to pollutants.
-
Mass Balance: A systematic evaluation of mass entering and exiting a system, vital for understanding pollutant dynamics.
-
Unsteady-State Systems: Systems where concentrations fluctuate over time, complicating predictions.
-
Box Model: A theoretical approach to simplifying complex systems for analysis.
Examples & Applications
Example of a well-mixed lake where a pollutant concentration is uniform until external factors cause changes.
Case study of a river where concentrations differ due to inflows from tributaries and discharges from industries.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a lake or river’s flow, pollutants may ebb and grow.
Stories
Once, a tiny fish named Polly worried about pollutants. As she swam through her lake, she observed how new pollutants entered, making her water uneasy. Polly learned the importance of tracking these changes.
Memory Tools
Remember C-MASS for pollutant modeling: Concentration, Mass, Accumulation, Sink, Source.
Acronyms
BOX for Box Model
Break it down
Organize
Xpredict.
Flash Cards
Glossary
- Concentration
The amount of a substance per defined space, often expressed as mass per unit volume.
- Mass Balance
A mathematical representation that accounts for the mass entering, leaving, and accumulating in a system.
- UnsteadyState
A condition where the concentration of a substance changes over time.
- Box Model
A simplified representation of a system where the environment is divided into compartments for easier analysis.
- Rate of Generation
The rate at which a substance is produced within a system.
- Rate of Loss
The rate at which a substance is removed from a system.
Reference links
Supplementary resources to enhance your learning experience.
