Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Mass Transfer Coefficients
Unlock Audio Lesson
Let's start our discussion on mass transfer coefficients. What do you think a mass transfer coefficient represents in the context of material movement between phases?
Is it a measure of how easily a substance can move from one phase to another, like from liquid to gas?
Exactly! The mass transfer coefficient quantifies the rate of transfer of a solute across an interface. It's influenced by flow conditions and the properties of both the solute and the surrounding fluids.
And does this mean there's a different coefficient for each phase?
Yes, good observation! We often denote these as k₁ for the liquid phase and k₂ for the gas phase. So, if we have an interface between water and air, each side will have its own coefficient.
I see! So, the overall transfer would need to account for both coefficients?
Absolutely! The overall mass transfer coefficient incorporates the individual phase coefficients and any resistances associated with them. It’s like a team effort!
Mass Transfer Resistance and Flux
Unlock Audio Lesson
Now, let's discuss mass transfer resistance. Why do you think it's important to understand where the resistance occurs in a mass transfer process?
Is it because it can help us improve the process by focusing on reducing that resistance?
That's correct! By identifying where the biggest resistance is, we can find ways to enhance the mass transfer rate. Can anyone recall what the common representation of flux is in mass transfer?
I think it's the concentration difference divided by the resistance?
Spot on! Let's say we denote flux as J; it’s driven by the concentration difference ΔC over the resistance R.
Is that why we talk about the resistance in series?
Exactly, by treating it as a series, we can model how the resistances of both phases contribute to the total mass transfer process. If one resistance is notably larger, it dominates the overall system.
Equilibrium and Driving Forces
Unlock Audio Lesson
Let's shift our focus to equilibrium. How does equilibrium play a role in mass transfer?
I guess it helps us figure out the concentration at the interface using known values from the bulk phases?
Exactly right! We can use relationships like Henry’s law to express these concentrations at the interface based on the bulk phase concentrations.
So basically, we are extrapolating the interim concentration since it’s hard to measure directly?
Correct! The fictional concentration at the interface allows us to derive formulas that include both equilibrium concepts and mass transfer coefficients.
This sounds quite powerful for engineering applications!
It certainly is! Understanding these relationships can help us optimize systems to enhance or control mass transfer effectively.
Application of Mass Transfer Equations
Unlock Audio Lesson
Now that we’ve covered the theory, let’s explore a potential application. How could knowing these equations help us in environmental engineering?
We might use them to understand how pollutants disperse from water into the air!
Exactly! By using the derived equations, we can predict how quickly a pollutant might transfer between phases and develop strategies to remediate water sources.
Can we also use this in chemical processes to enhance production?
Yes! Engineers often seek to manipulate mass transfer to improve reaction rates or yields. It’s a key consideration in chemical manufacturing.
Do we always need to know both phase coefficients then?
Typically yes, knowing both helps in accurately predicting the overall efficiency of mass transfer. Remember: it’s all about balancing those resistances.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers the principles of mass transfer across interfaces, introducing the overall mass transfer coefficient and its relationship with individual phase coefficients. It explains the concept of mass transfer resistance in different phases and illustrates how equilibrium is used to derive mass transfer equations.
Detailed
Derivation of Mass Transfer Equations
In this section, we delve into the complexities of mass transfer across interfaces, particularly focusing on the transfer of solutes between two phases, such as water and air. We start by defining the overall mass transfer coefficient and its dependence on flow and fluid properties. Notably, we emphasize that mass transfer resistance is localized near the interface between phases, leading us to model systems as having both a well-mixed bulk phase and a resistance zone at the interface.
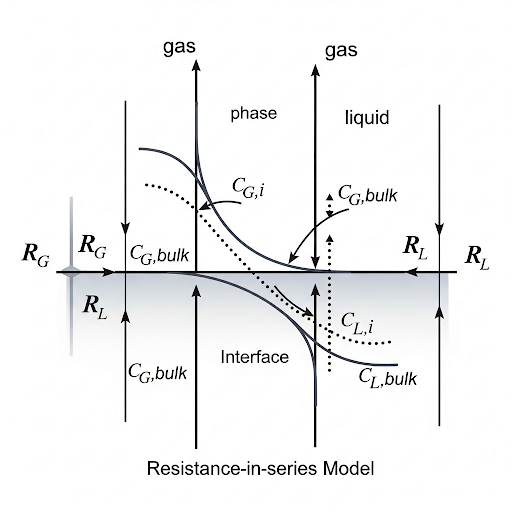
The section outlines the flow of mass (flux) defined by the concentration gradient between the phases and suggests that the concentration at the interface is difficult to measure directly. Thus, we evoke a resistance-in-series approach to connect the overall flux to measurable concentrations in the bulk phases, creating a relationship mediated by equilibrium states, characterized effectively by Henry's law. This leads to the derivation of equations that describe mass transfer as a combination of individual resistances in the liquid and gas phases, signifying that the overall resistance is determined by the controlling phase. Finally, the text discusses methods to calculate the mass transfer coefficients, showcasing the significance of understanding and manipulating resistance in engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Transfer Across Interfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we were discussing mass transfer across interfaces. We were discussing the general principles of mass transfer coefficient. So we defined something called as mass transfer coefficient and its dependency on the flow, the properties of the fluid and properties of the solute itself to some extent. So we stopped at a point where we were looking at transfer across an interface. So let us say there is an interface between two phases, let us say this is water and this is air. If mass transfer is happening from water to air, the transfer of A is going from water to air, which means there is a gradient from water to air.
Detailed Explanation
This chunk introduces the concept of mass transfer, particularly across interfaces between different phases, like water and air. The mass transfer coefficient is essential as it helps to describe how substances move from one phase to another. In this case, the movement of a solute (let’s call it A) is discussed, highlighting that a concentration gradient exists from the water phase to the air phase. The idea that mass transfer occurs when there's a difference in concentration between two phases is fundamental.
Examples & Analogies
Think of mass transfer like a sponge soaking up water. When you start with a dry sponge and dip it into water, water moves from the surrounding into the sponge, assuming the sponge's capacity is limited. The more the sponge is in contact with water (the gradient), the quicker it absorbs water. This illustrates how mass transfer works, where the gradient (difference in concentration) drives the movement of substances.
Mass Transfer Resistance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we also discussed that close to the fluid interface, it is convenient for us to assume that there is a region of mass transfer resistance. So the rest of the region is considered as well mixed or we call it as a bulk. By definition, when we say well mixed, the concentration here is constant.
Detailed Explanation
This chunk explains that near the interface between two phases, there tends to be a zone where resistance to mass transfer exists. This is because the concentration of the solute can change sharply near the boundary, while in the bulk regions away from the interface, the solution is assumed to be well mixed and uniform. This concept of mass transfer resistance is crucial for understanding how effectively a solute can move through the interface.
Examples & Analogies
Imagine you are pouring syrup into water. Initially, there's a concentrated layer of syrup at the top, but with time, the water mixes and becomes uniform. The area where the syrup meets the water is where the mixing or 'mass transfer' resistance happens—the syrup has to overcome the resistance of this boundary to evenly distribute throughout the water.
Calculating Mass Transfer Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, if we want to predict what is the flux, we need to know certain concentration values. However, often the accurate interface concentration is difficult to estimate. Instead, we can use the bulk concentrations and apply certain equations.
Detailed Explanation
Calculating mass transfer flux refers to determining the amount of solute moving across a unit area over time. We can’t always directly measure the concentration at the interface, but we can use the measured concentrations in the bulk phases to create equations that allow us to estimate the flux. This approach is a practical workaround to the difficulty of measuring interface concentrations directly.
Examples & Analogies
Imagine trying to gauge how much perfume is wafting into the air from a bottle. You can't measure the exact concentration where the two phases meet, but you can easily measure how much perfume is in the bottle and the scent in the room. By knowing these two values, you can estimate how much is moving into the air.
Resistance in Series Approach
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What we can do is invoke what is called a resistance in series approach. This means if we cannot directly relate the two concentrations, we can express it in terms of the resistances from each phase and rewrite our equations accordingly.
Detailed Explanation
The resistance in series approach helps us to model the mass transfer process by breaking it into individual resistances from each phase involved (like liquid and gas). Instead of trying to relate concentrations directly, we express the relationship through the individual resistances, ultimately leading to a combined resistance that gives us a clearer picture of the total mass transfer process.
Examples & Analogies
Think of this like the different hurdles in a relay race. Each runner (representing an individual resistance) has to pass the baton (mass transfer) to the next. The cumulative time it takes for the baton to go from the first to the last runner reflects the overall efficiency of the relay, similar to the cumulative effect of resistances in mass transfer.
Overall Mass Transfer Resistance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The overall rate of transport is a combination of the resistances in both phases, meaning that the process can be controlled by the slower phase (the one with the greater resistance).
Detailed Explanation
Mass transfer happens at a rate determined by the phase with the greater resistance. If one phase (like the gas) has a much lower resistance compared to another (like the liquid), that phase will not significantly influence the overall rate of mass transfer. Therefore, understanding which phase has the greatest resistance is crucial for optimizing mass transfer processes.
Examples & Analogies
Consider a smooth highway and a narrow, bumpy road that leads to your destination. If most of your travel time is spent on the bumpy road, it doesn't matter how fast you can drive on the highway; your overall speed is dictated by the slower path. Similarly, in mass transfer, the phase with the highest resistance will dictate the overall transport rate.
Practical Implications and Control Strategies
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Based on this understanding of resistances, we can determine which aspect of the system controls mass transfer. Depending on the context, we may want to increase or decrease mass transfer by modifying resistance factors.
Detailed Explanation
By understanding which resistance controls mass transfer, engineers can devise strategies to enhance or hinder the mass transfer process as required. For instance, in environmental situations, we may aim to reduce mass transfer to prevent the spread of pollutants, whereas in industrial applications, enhancing mass transfer may be desirable for efficiency.
Examples & Analogies
Think of cooking: if you want to speed up the cooking of a stew, you might increase the heat (reduce resistance) or stir it frequently to ensure even cooking. Conversely, if you're trying to keep a dish warm without cooking it further, you would lower the heat (increase resistance) to prevent overcooking. This is analogous to managing mass transfer in different scenarios.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Transfer Coefficient: A key variable indicating solute transfer rate between two phases.
-
Flux: Represents the mass transfer rate per unit area driven by concentration differences.
-
Mass Transfer Resistance: Opposition encountered based on phases that affect transfer rates.
-
Equilibrium: A balanced state crucial for deriving relationships in mass transfer calculations.
-
Henry’s Law: A critical relationship for predicting solute concentration across phases.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In environmental engineering, understanding mass transfer allows us to predict how pollutants will disperse from waterways into the atmosphere.
-
In chemical production, optimizing mass transfer rates can significantly enhance product yields and reaction efficiencies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mass transfer coefficient flows, as liquid and gas interaction grows.
📖 Fascinating Stories
-
Imagine a race where water and air compete, but the real winner is the substance transitioning between them, showcasing how mass transfer coefficients determine the champion of flow across interfaces.
🧠 Other Memory Gems
-
M-F-L-EH (Mass Transfer - Flux - Liquid/Gas - Equilibrium - Henry's Law) to remember the key components of mass transfer.
🎯 Super Acronyms
Co-F-R-E (Coefficient - Flux - Resistance - Equilibrium) for quick recall of key mass transfer concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Transfer Coefficient
Definition:
A measure of the transfer rate of a solute between phases, influenced by flow and fluid properties.
-
Term: Flux
Definition:
The rate of transfer of mass per unit area, driven by concentration gradients.
-
Term: Mass Transfer Resistance
Definition:
The opposition to mass transfer, which can vary between different phases.
-
Term: Equilibrium
Definition:
A state where the concentrations of constituents in different phases balance each other out.
-
Term: Henry’s Law
Definition:
A principle that relates the concentration of a solute in one phase to its concentration in another at equilibrium.