Mass Transfer Across Interfaces
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Transfer Coefficients
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome class! Today, we'll learn about mass transfer coefficients. Can anyone tell me what they think mass transfer coefficients represent in our context?

Is it the rate at which a substance moves from one phase to another?

Exactly! They quantify how effectively a mass transfer occurs between phases. Remember, different factors, like the flow and properties of the fluid, affect these coefficients.

So, higher coefficients mean better mass transfer?

Yes, that's correct! Think of the acronym 'FAST'—Favorable flow, Area of interface, Solute properties, and Temperature influence the speed of transfer.

What are the specific roles of these factors again?

Good question! The flow influences how quickly molecules reach the interface, while solute properties can dictate how easily they move into the new phase.

So we can optimize these factors to improve environmental processes?

Exactly! This optimization is crucial in applications like remediation of polluted water.

In summary, mass transfer coefficients indicate the efficiency of mass transfer. Key factors include flow, area, properties of solute and temperature.
Mass Transfer Resistance
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s dive deeper into mass transfer resistance. Can anyone explain its significance?

I think it affects how quickly mass transfer can happen?

Exactly! High resistance means lower flux. In a system involving two phases, like water and air, we have resistance in both the liquid and gas phases. Can you recall what happens at the interface?

There’s a gradient, and mass transfer resistance is highest there?

Correct! All mass transfer happens across this interface, creating a concentration gradient. We’ll use the term 'equilibrium' to describe the state where concentrations in both phases balance out.

How do we mathematically express those resistances?

Great question! We can express the total resistance as a series of the individual resistances of both phases: R_total = R_liquid + R_gas. Then mass transfer flux can be computed from this.

So optimizing the phase with the higher resistance improves overall flux?

Exactly! Always target the highest resistance to enhance the entire mass transfer process.

To recap, mass transfer resistance occurs at interfaces and influences flux. We calculate total resistance in series for both phases.
Estimating Flux Using Henry's Law
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s explore how we can use Henry’s law to estimate flux across an interface. Who can summarize what Henry’s law states?

It relates the concentration of a solute in one phase to its concentration in another phase at equilibrium?

Exactly! It informs how one concentration can be used to predict the other. This can help simplify our calculations when determining mass transfer coefficients.

So we can say if we know the concentration in the gas phase, we can infer the concentration in the liquid phase?

That's right! We represent this through the equation: C_A1 = k_H * C_A2, where k_H is Henry's constant. And what does that mean for our calculations?

It gives us a way to express interface concentrations without directly measuring them?

Spot on! This eases the difficulty of obtaining accurate interface concentrations. Remember, we often rely on these estimations to compute total flux more effectively.

How can we practically apply these results?

You’ll use these calculations to assess the effectiveness of environmental remediation strategies by measuring concentrations in bulk phases to evaluate the impact on overall transfer.

To summarize, Henry's law lets us correlate concentrations between phases, aiding in estimating interface concentrations for flux computations.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section discusses the principles of mass transfer coefficients, the resistance encountered during mass transfer across fluid interfaces, and how to estimate flux through the use of equilibrium relationships and resistance in series. Key challenges associated with measuring interface concentrations are also addressed.
Detailed
Detailed Summary
In this section, we explore the critical principles surrounding mass transfer across interfaces, specifically focusing on the interaction between different phases, such as air and water. The concept of mass transfer coefficients is introduced, emphasizing how they are influenced by fluid properties, flow characteristics, and solute properties.
Mass transfer occurs across an interface when a solute moves from one fluid phase to another, creating gradients between the concentrations. Near this interface, mass transfer resistance is assumed, with the rest of the system being well-mixed or at a constant concentration. The section explains the complexities of measuring interface concentrations and the reliance on bulk measurements.
To tackle the challenge of estimating interfacial flux, the resistance in series approach is discussed, which incorporates mass transfer resistances from both the liquid and gas phases. Furthermore, the section outlines the use of Henry’s law to express the relationship between gas and liquid concentrations at equilibrium, thus enabling the determination of the overall mass transfer coefficient and equations to compute flux.
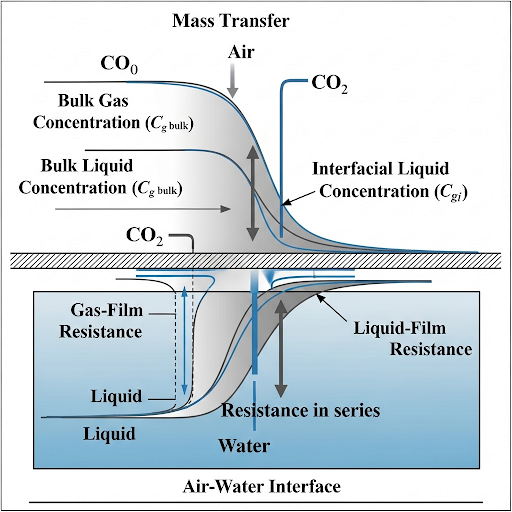
Overall, this section is vital for understanding how mass transfer processes can be manipulated and optimized in both environmental and industrial contexts.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Mass Transfer Across Interfaces
Chapter 1 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, we were discussing mass transfer across interfaces. We were discussing the general principles of mass transfer coefficient.
Detailed Explanation
This chunk introduces the concept of mass transfer across interfaces and mentions that the focus is on the mass transfer coefficient. The mass transfer coefficient is a crucial parameter that quantifies the rate of mass transfer during processes such as evaporation or diffusion between two different phases, like liquid and gas. Understanding its principles helps in predicting how substances move across these interfaces.
Examples & Analogies
Think of mass transfer like water flowing through a filter. The filter represents the interface, and the water that passes through it represents the mass being transferred. The efficiency of the filter is akin to the mass transfer coefficient—different filters (or transfer media) allow water to pass through at different rates.
Understanding Interfaces
Chapter 2 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So let us say there is an interface between two phases, let us say this is water and this is air. If mass transfer is happening from water to air, the transfer of A is going from water to air, which means there is a gradient from water to air.
Detailed Explanation
This chunk discusses the specific scenario of mass transfer occurring between two phases: water (liquid) and air (gas). The phrase 'transfer of A' indicates a substance (A) that is moving from one phase to another. The mention of a gradient highlights the concentration difference that drives mass transfer; substances naturally move from areas of higher concentration to areas of lower concentration.
Examples & Analogies
Imagine a sponge soaked in water. If you hold it over a dry surface, the water will begin to transfer to the air due to evaporation, creating a concentration gradient. Just like the sponge loses water, substances move from areas of high concentration (sponge) to low concentration (air).
Mass Transfer Resistance and Coefficient
Chapter 3 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So we also discussed that close to the fluid interface, it is convenient for us to assume that there is a region of mass transfer resistance.
Detailed Explanation
This chunk explains the concept of mass transfer resistance occurring near the interface between two phases. This resistance refers to the difficulty substances face while transitioning across the interface. The mass transfer coefficient can vary based on fluid properties, flow conditions, and characteristics of the solute, affecting how quickly the solute can move from one phase to another.
Examples & Analogies
Consider trying to pour syrup into water. The syrup flows slowly because it is thick; this thickness is similar to mass transfer resistance, which affects how quickly substances can transfer through an interface.
Flux Definition
Chapter 4 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So we also defined that the flux can be defined as J = kA(c_A,interface - c_A) and J = kB(c_B - c_B,interface).
Detailed Explanation
In this chunk, the equation representing flux (J) is introduced. Flux is a measure of the quantity of substance that passes through a unit area per unit time. The equation shows that the flux depends on the concentration difference across the interface and the mass transfer coefficient associated with each phase. Understanding this helps predict how fast a substance will move across an interface.
Examples & Analogies
Think of flux as the flow of traffic. The mass transfer coefficient represents how wide the road is, and the concentration difference represents how many cars (substances) want to cross the intersection. A wider road (higher mass transfer coefficient) allows more cars to pass quickly (higher flux).
Challenges in Measuring Interface Concentration
Chapter 5 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
And the problem sometimes is we cannot, we do not know what c_A,interface is.
Detailed Explanation
This chunk highlights a common issue in mass transfer analysis: the difficulty in determining the concentration at the interface (c_A,interface). In many situations, especially when dealing with multiple phases or solutes, estimating this concentration is challenging. This uncertainty can lead to inaccuracies in predicting flux.
Examples & Analogies
Imagine trying to measure the temperature at the surface of a bubbling pot of water. It's hard to assess the exact temperature right at the surface due to the steam and movement, much like it's difficult to measure the concentration at an interface in mass transfer.
Resistance in Series Approach
Chapter 6 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So we invoke what is called as a resistance in series approach to do this.
Detailed Explanation
This chunk introduces the resistance in series approach, which is a method to simplify understanding mass transfer across interfaces when direct measurements at the interface are not possible. By treating the resistances from both phases as resistors in series, it allows for easy calculation of total resistance and flux.
Examples & Analogies
Think of water flowing through a series of filters, each with different resistances. If you know how each filter affects the flow, you can estimate the total flow rate through the combined system, just like using the resistance in series approach helps calculate total mass transfer.
Overall Mass Transfer Equation
Chapter 7 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is very useful representation. So, this resistance is a series.
Detailed Explanation
This piece discusses the practical application of the overall mass transfer equation, emphasizing that the total mass transfer resistance can be understood as a combination of individual resistances from both phases. This concept is vital for engineering applications, where knowing which resistance dominates can guide decisions on adjusting processes for increased efficiency.
Examples & Analogies
Consider lining up in a queue at a store. If one person moves slower than the others, they control the speed at which the entire line moves, reflecting how the phase with the highest resistance dictates the overall mass transfer rate.
Impact of Resistance Values
Chapter 8 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For example, in this case if I calculate R1 = 1000 and R2 = 10.
Detailed Explanation
In this chunk, specific examples illustrate how varying resistance values can affect overall mass transfer rates. An analysis is performed showing that one much larger resistance can dominate the total resistance, thereby controlling the mass transfer process.
Examples & Analogies
Imagine trying to push a heavy box through a narrow door. Even if the box can slide easily through open air, if the door is too small (high resistance), it becomes the bottleneck and limits how fast you can move the box through.
Conclusion on Mass Transfer Coefficients
Chapter 9 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now how do we estimate the mass transfer coefficient?
Detailed Explanation
The final chunk emphasizes the importance of estimating mass transfer coefficients as they are essential for calculating flux at the interface. It explains the underlying principles that guide the estimation process and implies that direct equations may not always be available, necessitating experimental data or empirical correlations.
Examples & Analogies
Consider a chef trying to determine the right seasoning for a dish. They may not have a recipe and have to taste and adjust based on experience and intuition, similar to how engineers might have to estimate mass transfer coefficients based on prior knowledge or experiments.
Key Concepts
-
Overall Mass Transfer Coefficient: Represents the combined efficiency of mass transfer across phases.
-
Resistance in Series: Concept of summing resistances from liquid and gas phases to calculate total mass transfer resistance.
Examples & Applications
The transfer of oxygen from the atmosphere into a body of water, where the concentration of oxygen varies between air and water.
In industrial applications, the absorption of pollutants from gas emissions into liquid scrubber solutions.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To measure the flux, we must know, / The mass transfer rate will surely show.
Stories
Imagine water at the beach absorbing oxygen from the air, where a child watches the bubbles rise. This is how mass transfer works across an interface.
Memory Tools
Remember 'FLAMES' for Mass Transfer: Flow, Liquid properties, Area, Mass transfer coefficient, Environment, and Speed.
Acronyms
‘MATRIX’ helps for mass transfer
Mass Transfer
Resistance
Area
Transfer Coefficient
Interfacial Gradient
and X equations.
Flash Cards
Glossary
- Mass Transfer Coefficient
A factor representing the rate at which a solute moves from one phase to another, influenced by fluid properties, flow, and temperature.
- Mass Transfer Resistance
The opposition to mass transfer across an interface, which can arise from different phases and is computed in series.
- Henry's Law
A principle yielding a linear relationship between the concentration of a gas in a liquid and its partial pressure above the liquid at equilibrium.
- Flux
The rate of flow of a property per unit area, often used to describe the movement of solutes across an interface.
Reference links
Supplementary resources to enhance your learning experience.
